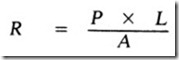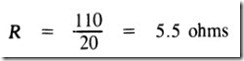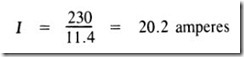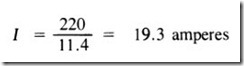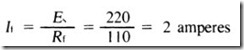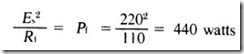Motor Calculations

Motor Calculations part1

The following simple calculations for motor circuits will serve to acquaint the reader with methods used in determining voltage drops, currents, and efficiency of de and ac motors.

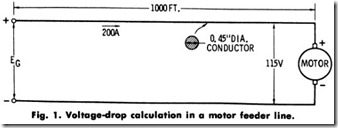
Problem-A 115- volt de motor draws a current of200 amperes and is located 1000 ft. from the supply source. If the copper transmission wire has a diameter of 0.45 inch, what must be the voltage of the supply source? See Fig. 1.

Solution-The resistance of any conductor varies directly with its length and inversely as its cross-sectional area. Therefore, the formula is

where,

R is the resistance in ohms,

P is the specific resistance of one mil. ft. of copper wire (10.4),

L is the length in feet,

A is the area in circular mils (diameter of wire in thousandths squared).

NOTE: The cross-sectional area of a circular conductor can be expressed in circular mils by squaring the diameter of the conductor expressed in thousandths. For example, a wire 0.625 inch in diameter has a circular-mil area of 625 x 625 = 390,625 circular mils.

Thus, the resistance of the feed lines is

and

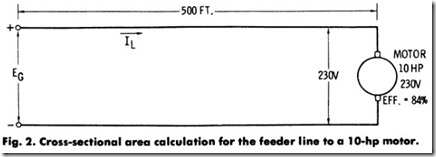
Problem-A 10-hp, 230-volt de motor of 84% full-load efficiency is located 500ft. from the supply mains. If the motor-starting current is 1.5times thefull-load current, what is the smallest cross-sectional area of copper wire required when the allowable voltage drop in the feeder at starting is 24 volts? See Fig. 2.

Solution-The motor full-load current is

Motor-starting current is

I_s = 38.6 x 1.5 = 57.9 amperes

Since the voltage drop in the feeder at starting is 24 volts, then, according to Ohm’s law

The minimum cross-sectional area is therefore

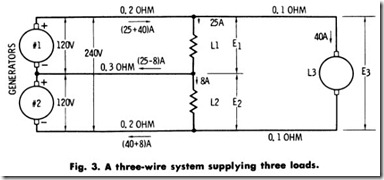
Problem-In the circuit of Fig. 3, with loads Lb Lz, and drawing currents of 25, 8, and 40 amperes, respectively, calculate:

(a) The power supplied by each generator.

(b) The voltages E₁, E₂ , and E₃ .

Solution-By inspection, the currents supplied by generators Nos. 1 and 2 are 65 and 48 amperes, respectively.

(a)

P_G1 = 120 X 65 = 7800 watts

P_G2 = 120 X 48 = 5760 watts

(b) According to Kirchhoff’s law

E₁ = 120 – (65 x 0.2) – (17 x 0.3) = 101.9 volts
E₂ = 120 + (17 x 0.3) – (48 x 0.2) = 115.5 volts

and

E₁ – E₂ = 217.4 volts

Similarly

E³= 217.4 – (0.2 x 40) = 209.4 volts

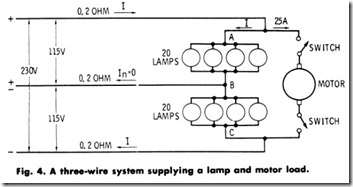
Problem-A three-wire system supplies the load shown in Fig. 4. If the resistance of each lamp is 110 ohms and the motor takes a current of 25 amperes, calculate the voltage across each group of lamps:

(a) When the motor is disconnected.

(b) When the motor is operating.

Solution-The combined resistance of a group of 20 lamps, each having a resistance of 110 ohms, is

Since the load is a balanced one, it is evident that the current in the neutral is zero.

The current through the lamps with the motor disconnected is

The current through the lamps with the motor operating and drawing 25 amperes can be obtained if Kirchhoff’s law is applied to the circuit,

remembering that the current flowing in the line is now (I + 25) amperes.

and

Thus, when the motor is thrown on the line, the voltage across the lamps will fall from 1II.I0 to 106.I5 volts.

Problem- Thefield winding of a shunt motor has a resistance of 110 ohms, and the voltage applied to it is 220 volts. What is the amount of power expended in the field excitation?

Solution-The current through the field is