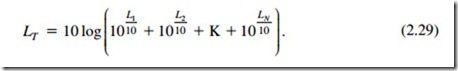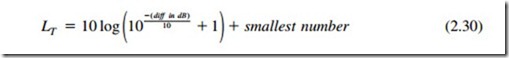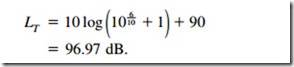Combining Decibels
Adding Decibel Levels
The sum of two or more levels expressed in dB may be found as follows:
If, for example, we have a noisy piece of machinery with an LP = 90dB and wish to turn on a second machine with an LP = 90dB, we need to know the combined LP. Because both measured levels are the result of the power being applied to the machine, with some percentage being converted into acoustic power, we can determine LT by using Eq. (2-33). Therefore
Doubling the acoustic power results in a 3 dB increase.
An alternative dB addition technique is given through the courtesy of Gary Berner.
Example
If we wish to add 90 dB to 96 dB, using Eq. (2-33), take the difference in dB (6 dB) and put it in the equation:
Input signals to a mixing network also combine in this same manner, but the insertion loss of the network must be subtracted. Two exactly phase-coherent sine wave signals of equal amplitude will combine to give a level 6 dB higher than either sine wave.
The general case equation for adding sound pressure, voltages, or currents is
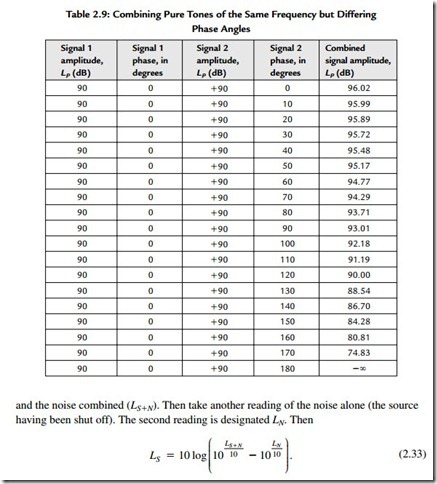
Table 2.9 shows the effects of adding two equal amplitude signals with different phases together using Eq. (2-36).
Subtracting Decibels
The difference of two levels expressed in dB may be found as follows:
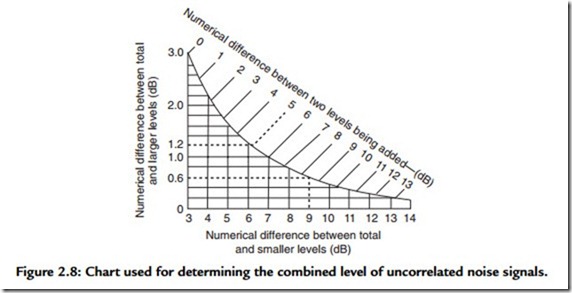
Combining Levels of Uncorrelated Noise Signals
When the sound level of a source is measured in the presence of noise, it is necessary to subtract out the effect of the noise on the reading. First, take a reading of the source
To Add Levels
Enter the chart with the numerical difference between the two levels being added (top of chart). Follow the line corresponding to this value to its intersection with the curved line and then move left to read the numerical difference between the total and larger levels. Add this value to the larger level to determine the total.
Example
To add 75 dB to 80 dB, subtract 75 dB from 80 dB; the difference is 5 dB. In Figure 2.8, the 5-dB line intersects the curved line at 1.2 dB on the vertical scale. Thus the total value is 80 dB + 1.2 dB, or 81.2 dB.
To Subtract Levels
Enter the chart in Figure 2.8 with the numerical difference between the total and larger levels if this value is less than 3 dB. Enter the chart with the numerical difference between the total and smaller levels if this value is between 3 and 14 dB. Follow the line corresponding to this value to its intersection with the curved line and then either left or down to read the numerical difference between total and larger (smaller) levels. Subtract this value from the total level to determine the unknown level.
Example
Subtract 81 dB from 90 dB; the difference is 9 dB. The 9-dB vertical line intersects the curved line at 0.6 dB on the vertical scale. Thus the unknown level is 90 dB – 0.6 dB, or 89.4 dB.