Losses in induction machines occur in windings, magnetic cores, besides mechanical friction and windage losses. They determine the efficiency of energy conversion in the machine and the cooling system that is required to keep the temperatures under control.
In the design stages, it is natural to try to calculate the various types of losses as precisely as possible. After the machine is manufactured, the losses have to be determined by tests. Loss segregation has become a standard method to determine the various components of losses, because such an approach does not require shaft-loading the machine. Consequently, the labor and energy costs for testings are low.
On the other hand, when prototyping or for more demanding applications, it is required to validate the design calculations and the loss segregation method. The input-output method has become standard for the scope. It is argued that, for high efficiency machines, measuring of the input and output Pin, Pout to determine losses Σp on load
Σp = Pin − Pout (11.1) requires high precision measurements. This is true, as for a 90% efficiency machine a 1% error in Pin and Pout leads to a 10% error in the losses.
However, by now, less than (0.1 to 0.2)% error in power measurements is available so this objection is reduced considerably.
On the other hand, shaft-loading the IM requires a dynamometer, takes time, and energy. Still, as soon as 1912 [1] it was noticed that there was a notable difference between the total losses determined from the loss segregation method (no-load + short – circuit tests) and from direct load tests. This difference is called “stray load losses.” The dispute on the origin of “stray load losses” and how to measure them correctly is still on today after numerous attempts made so far. [2 – 8]
To reconcile such differences, standards have been proposed. Even today, only in the USA (IEEE Standard 112B) the combined loss segregation and input-output tests are used to calculate aposteriori the “stray load losses” for each motor type and thus guarantee the efficiency.
In most other standards, the “stray load losses” are assigned 0.5 or 1% of rated power despite the fact that all measurements suggest much higher values.
The use of static power converters to feed IMs for variable speed drives complicates the situation even more, as the voltage time harmonics are producing additional winding and core losses in the IM.
Faced with such a situation, we decided to retain only the components of losses which proved notable (greater than (3 to 5%) of total losses) and explore their computation one by one by analytical methods.
Further on numerical, finite element, loss calculation results are given.
11.1. LOSS CLASSIFICATIONS
The first classification of losses, based on their location in the IM, includes:
• Winding losses – stator and rotor
• Core losses – stator and rotor
• Friction & windage losses – rotor
Electromagnetic losses include only winding and core losses.
A classification of electromagnetic losses by origin would include
• Fundamental losses
• Fundamental winding losses (in the stator and rotor)
• Fundamental core losses (in the stator)
• Space harmonics losses
• Space harmonics winding losses (in the rotor)
• Space harmonic core losses (stator and rotor)
• Time harmonic losses
• Time harmonics winding losses (stator and rotor)
• Time harmonic core losses (stator and rotor)
Time harmonics are to be considered only when the IM is static converter fed, and thus the voltage time harmonics content depends on the type of the converter and the pulse width modulation used with it. The space harmonics in the stator (rotor) mmf and in the airgap field are related directly to mmf space harmonics, airgap permeance harmonics due to slot openings, leakage, or main path saturation.
All these harmonics produce additional (stray) core and winding losses called
• Surface core losses (mainly on the rotor)
• Tooth flux pulsation core losses (in the stator and rotor teeth)
• Tooth flux pulsation cage current losses (in the rotor cage)
Load, coil chording, and the rotor bar-tooth contact electric resistance (interbar currents) influence all these stray losses.
No-load tests include all the above components, but at zero fundamental rotor current. These components will be calculated first; then corrections will be applied to compute some components on load.
11.2. FUNDAMENTAL ELECTROMAGNETIC LOSSES
Fundamental electromagnetic losses refer to core loss due to space fundamental airgap flux density– essentially stator based–and time fundamental conductor losses in the stator and in the rotor cage or winding.
The fundamental core losses contain the hysteresis and eddy current losses in the stator teeth and core,
PFe1 ≈ C fh 1 B1ts n Gteeth + B1cs n Gcore +
1 1
2 2 2 (11.2)
![]()
![]() + C fe 1 B1ts Gteeth + B1cs Gcore
+ C fe 1 B1ts Gteeth + B1cs Gcore
1 1
where Ch [W/kg], Ce [W/kg] n = (1.7 – 2.0) are material coefficients for hysteresis and eddy currents dependent on the lamination hysteresis cycle shape, the electrical resistivity, and lamination thickness; Gteeth and Gcore, the teeth and back core weights, and B1ts, B1cs the teeth and core fundamental flux density values.
At any instant in time, the flux density is different in different locations and, in some regions around tooth bottom, the flux density changes direction, that is, it becomes rotating.
Hysteresis losses are known to be different with alternative and rotating, respectively, fields. In rotating fields, hysteresis losses peak at around 1.4 to 1.6 T, while they increase steadily for alternative fields.
Moreover, the mechanical machining of stator bore (when stamping is used to produce slots) is known to increase core losses by, sometimes, 40 to 60%. The above remarks show that the calculation of fundamental core losses is not a trivial task. Even when FEM is used to obtain the flux distribution, formulas like (11.2) are used to calculate core losses in each element, so some of the errors listed above still hold. The winding (conductor) fundamental losses are
Pco = 3R Is 1s2 + 3R Ir 1r2 (11.3)
The stator and rotor resistances Rs and Rr’ are dependent on skin effect. In this sense Rs(f1) and Rr’(Sf1) depend on f1 and S. The depth of field penetration in copper δCo(f1) is
![clip_image001[4] clip_image001[4]](http://machineryequipmentonline.com/electric-equipment/wp-content/uploads/2017/04/clip_image0014_thumb8.gif)
![]() δCo( )f1 = µ0 2π σ2f1 Co = 1.256 10⋅ −622π60 f1 = 0.94 10⋅ −2 60f1 m (11.4) 60
δCo( )f1 = µ0 2π σ2f1 Co = 1.256 10⋅ −622π60 f1 = 0.94 10⋅ −2 60f1 m (11.4) 60
If either the elementary conductor height dCo is large or the fundamental frequency f1 is large, whenever
δCo > d2Co (11.5) the skin effect is to be considered. As the stator has many layers of conductors in slot even for δCo ≈ dCo/2, there may be some skin effect (resistance increase). This phenomenon was treated in detail in Chapter 9.
In a similar way, the situation stands for the wound rotor at large values of slip S. The rotor cage is a particular case for one conductor per slot. Again, Chapter 9 treated this phenomenon in detail. For rated slip, however, skin effect in the rotor cage is, in general, negligible.
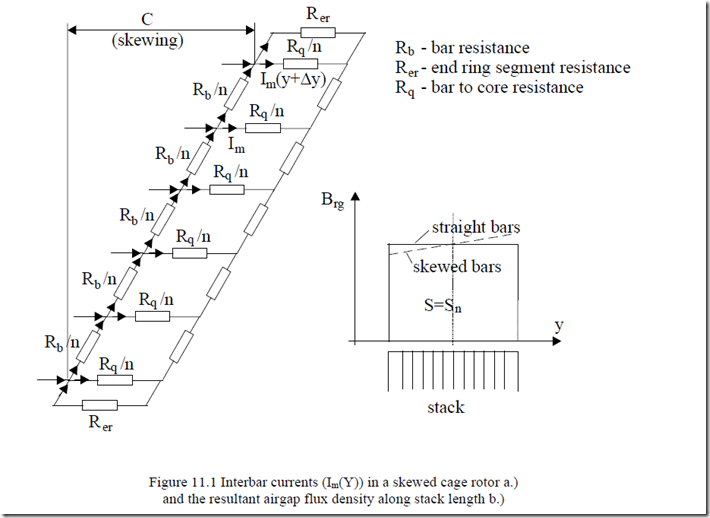
In skewed cage rotors with uninsulated bars (cast aluminum bars), there are interbar currents (Figure 11.1a).
The treatment of various space harmonics losses at no-load follows.
Depending on the relative value of the transverse (contact) resistance Rq and skewing c, the influence of interbar currents on fundamental rotor conductor losses will be notable or small.
The interbar currents influence also depends on the fundamental frequency as for f1 = 500 Hz, for example, the skin effect notably increases the rotor cage resistance even at rated slip.
On the other hand, skewing leaves an uncompensated rotor mmf (under load) which modifies the airgap flux density distribution along stack length (Figure 11.1b).
As the flux density squared enters the core loss formula, it is obvious that the total fundamental core loss will change due to skewing.
As skewing and interbar currents also influence the space harmonics losses, we will treat their influence once for all harmonics. The fundamental will then become a particular case.
Fundamental core losses seem impossible to segregate in a special test which would hold the right flux distribution and frequency. However a standstill test at rated rotor frequency f2 = Sf1 would, in fact, yield the actual value of Rr’(Snf1). The same test at various frequencies would produce precise results on conductor fundamental losses in the rotor. The stator fundamental conductor losses might be segregated from a standstill a.c. single-phase test with all phases in series at rated frequency as, in this case, the core fundamental and additional losses may be neglected by comparison.
11.3. NO-LOAD SPACE HARMONICS (STRAY NO-LOAD) LOSSES IN NONSKEWED IMs
Let us remember that airgap field space harmonics produce on no-load in nonskewed IMs the following types of losses:
• Surface core losses (rotor and stator)
• Tooth flux pulsation core losses (rotor and stator)
• Tooth flux pulsation cage losses (rotor)
The interbar currents produced by the space harmonics are negligible in nonskewed machines if the rotor end ring (bar) resistance is very small (Rcr/Rb < 0.15).
11.3.1. No-load surface core losses
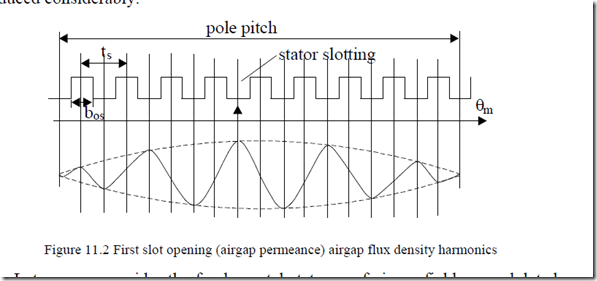
As already documented in Chapter 10, dedicated to airgap field harmonics, the stator mmf space harmonics (due to the very placement of coils in slots) as well the slot openings produce airgap flux density harmonics. Further on, main flux path heavy saturation may create third flux harmonics in the airgap.
It has been shown in Chapter 10 that the mmf harmonics and the first slot opening harmonics with a number of pole pairs νs = Ns ± p1 are attenuating and augmenting each other, respectively, in the airgap flux density.
For these mmf harmonics, the winding factor is equal to that of the fundamental. This is why they are the most important, especially in windings with chorded coils where the 5th, 7th, 11th, and 17th stator mmf harmonics are reduced considerably.
Let us now consider the fundamental stator mmf airgap field as modulated by stator slotting openings (Figure 11.2).
s± 1 (θm ,t)= µ0F aa10m 1 cos(ω1t − p1θm )cos Nsθm (11.6)
BN p
This represents two waves, one with Ns + p1 pole pairs and one with Ns – p1 pole pairs, that is, exactly, the first airgap magnetic conductance harmonic. Let us consider that the rotor slot openings are small or that closed rotor slots are used. In this case, the rotor surface is flat.
The rotor laminations have a certain electrical conductivity, but they are axially insulated from each other by an adequate coating.
For frequencies of 1,200 Hz, characteristic to Ns ± p1 harmonics, the depth of field penetration in silicon steal for µFe = 200 µ0 is (from 11.4) δ ≈ 0.4 mm, for 0.6 mm thick laminations. This means that the skin effect is not significant. Therefore we may neglect the rotor lamination-induced current reaction to the stator field. That is, the airgap field harmonics (11.6) penetrate the rotor without being disturbed by induced rotor surface eddy currents. The eddy currents along the axial direction are neglected.
But now let us consider a general harmonic of stator mmf produced field Bνg.
As expected, with semiclosed slots, a1 and a2 become much smaller; also, the Carter coefficient decreases. Consequently, the rotor surface losses will be much smaller. Also, increasing the airgap has the same effect. However, at the price of larger no-load current and lower power factor of the machine. The stator surface losses produced by the rotor slotting may be calculated in a similar way by replacing F1(bos/ts), F2(bos/ts), β(bos/g) with β(bor/g), F1(bor/ts),
F2(bor/ts), and Ns/p1 with Nr/p1.
As the rotor slots are semiclosed, bor << bos, the stator surface losses are notably smaller than those of the rotor, They are, in general, neglected.