Leakage saturation influence on synchronous torques

The airgap field produced by the first rotor mmf slot harmonic ν = ±’ ^Nr +1 p₁ due to the airgap magnetic conduction fluctuation caused by leakage saturation (second term in (10.19)) is

Bgν’ = µ0F2νm ⋅cos± Np1r +1θ m(ω ±1 NrΩr )t ⋅ a ‘g0 sin 2( θ − ω1t) (10.69) 

NrΩr )t ⋅ a ‘g0 sin 2( θ − ω1t) (10.69) 

If B_gν contains harmonic (term) multiplied by cos(νθ m ω₁t) for any n =

±6c₁ + 1 that corresponds to the stator mmf harmonics, a synchronous torque condition is again obtained. Decomposing (10.69) into two terms we find that only if

^Np₁^r ± 3 ≠ (6c₁ ±1) (10.70)

such torques are avoided. Condition (10.70) becomes

N_r ≠ 2p 3c₁( ₁ m1); c₁ =1,2,3,… (10.71)

The largest such torque occurs in interaction with the first stator slot mmf harmonic ν =₁ ^N_p1^s ±1 unless

	Ns ±1≠ Nr ± 3 p1 p1	(10.72)
So,	Nr ≠ Ns m 4p1	(10.73)

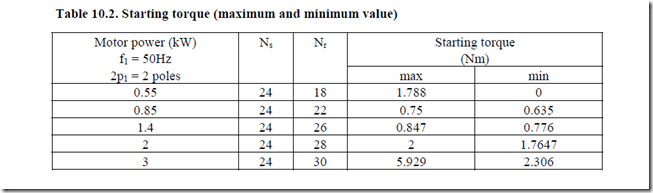
As an evidence of the influence of synchronous torque at standstill with rotor bars skewed by one stator slot pitch, some experimental results are given on Table 10.2. [1]

As Table 10.2 shows the skewing of rotor bars cannot prevent the occurrence of synchronous torque and a small change in the number of rotor slots drastically changes the average starting torque. The starting torque variation (with rotor position) is a clear indication of synchronous torque presence at stall.

The worst situation occurs with N_r = 18 = 6c₁p₁ (10.65). The speed for this synchronous torque comes from (10.69) as

± ω +3 ₁ N_rΩ = ±ω_{r 1} (10.74) or

Ω = ±_r ⁴N^ω_r ; n ^{= 4}N^f1_r (10.75)

Calculating the synchronous torques (even at zero speed) analytically is a difficult task. It may be performed by calculating the stator mmf harmonics airgap field interaction with the pertinent rotor current mmf harmonic.

After [1], the maximum tangential force fθ_max per unit rotor area due to synchronous torques at standstill should be

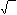()²

µ0 n Is s 2 d (10.76)

fθ max ≈ 4γslot

where n I_{s s} 2 is the peak slot mmf, γ_slot is the stator slot angle, and d is the greatest common divisor of N_s and N_r.

From this point of view, the smaller d, the better. The number d = 1 if Ns and Nr are prime numbers and it is maximum for N_s = N_r = d.

With N_s = 6p₁q₁, for q integer, that is an even number with N_r an odd number, with d = 1 the smallest variation with rotor position (safest start) of starting torque is obtained.

However, with N_r an odd number, the IM tends to be noisy, so most IMs have an even number of rotor slots, but with d = 2 if possible.

10.9.4. The secondary armature reaction

So far in discussing the synchronous torques, we considered only the reaction of rotor currents on the fields of the fundamental stator current. However, in some cases, harmonic rotor currents can induce in the stator windings additional currents of a frequency different from the power grid frequency. These additional stator currents may influence the IM starting properties and add to the losses in an IM. [4,5] These currents are related to the term of secondary armature reaction. [4]

With delta stator connection, the secondary armature reaction currents in the primary windings find a good path to flow, especially for multiple of 3 order harmonics. Parallel paths in the stator winding also favor this phenomenon by its circulating currents.

For wound (slip ring) rotor IMs, the field harmonics are not influenced by delta connection or by the parallel path. [6] Let us consider the first step (slot)

^{stator harmonic N}p1^s ±1 whose current I_{1 } Np1s ±1 produces a rotor current I₂ _ Np1s ±1 .

I1 Np1s ±1 (10.77)

I2

 p1  d  Np1s ±1_

τ_d is the differential leakage coefficient for the rotor cage. [1]

τd  N = π(NNs ±r p1 ) 2 ⋅ sin 2 π(N1 s ± p1 ) −1 (10.78)



 p

 N_r 

As known, N_s and N_r are numbers rather close to each other, so τ_{d } _Np1s ±1_

might be a large number and thus the rotor harmonic current is small. A strong secondary armature reaction may change this situation drastically. To

demonstrate this, let us notice that I_2 Ns ±1 can now create harmonics of order ν′

 p1  

 ^Ns ±1 :

(10.46), for c₂ = 1 and ν = _ p1 _

ν =’ N1r ±  Np1s ±1 p The ν′ rotor harmonic mmf Fν′ has the amplitude:	(10.79)
Fν’ = F2  ⋅	(10.80)

^{ }

 p1 ±1 N_r N_s p₁  Ns

If these harmonics induce notable currents in the stator windings, they will,

in fact, reduce the differential leakage coefficient from ^τ_{d } _{Ns ±1}_ to τ’_{d  Np1s ±1}_ . [1]

_{p1 }



− N −Ns ± p1 2

τ’d _ _Np1_s ±1 ≈ τd _ _Np1_s ±1  r (Ns ± p1 ) (10.81)

Now the rotor current I_2 Ns ±1 of (10.77) will become I’_2 Ns ±1 .

 p1   p1 

I1 Ns ±1

I1 Ns ±1

I’2_ Np1_s ±₁ ^{= τ}‘_d^_^pN¹s ±1^^ (10.82)

 p1 

The increase of rotor current I’_2 Ns ±1 is expected to increase both

 p1  asynchronous and synchronous torques related to this harmonic.

In a delta connection, such a situation takes place. For a delta connection, the rotor current (mmf) harmonics

ν =’ ^Np ^{r −} ^Np1^s ±1^_ = 3c c =1,3,5,… (10.83)

1 _

can flow freely because their induced voltages in the three stator phases are in phase (multiple of 3 harmonics). They are likely to produce notable secondary armature reaction.

To avoid this undesirable phenomenon,

N_s − N_r ≠ (3c m1)p₁ = 2p ,4p_{1 1},… (10.84)

An induction motor with 2p₁ = 6, N_s = 36, N_r = 28 slots does not satisfy (10.84), so it is prone to a less favourable torque-speed curve in ∆ connection than it is in star connection.

In parallel path stator windings, circulating harmonics current may be responsible for notable secondary armature reaction with star or delta winding connection.

These circulating currents may be avoided if all parallel paths of the stator winding are at any moment at the same position with respect to rotor slotting. However, for an even number of current paths, the stator current harmonics of the order ^{Nr − Ns} −1 or ^{Nr − Ns} +1 may close within the winding if the p1 p1 p1 p1

two numbers are multiples of each other. The simplest case occurs if

N_s − N_r = 3p₁ (10.85)

When (10.85) is fulfilled, care must be exercised in using parallel path stator windings.

We should also notice again that the magnetic saturation of stator and rotor teeth lead to a further reduction of differential leakage by 40 to 70%.

10.9.5. Notable differences between theoretical and experimental torque/speed curves

By now the industry has accumulated enormous data on the torque/speed curves of IM of all power ranges.

In general, it was noticed that there are notable differences between theory and tests especially in the braking regime (S > 1). A substantial rise of torque in the braking regime is noticed. In contrast, a smaller reduction of torque in the large slip motoring regime appears frequently.

A similar effect is produced by transverse (lamination) rotor currents between skewed rotor bars.

However, in this latter case, there should be no difference between slip ring and cage rotor, which is not the case in practice.

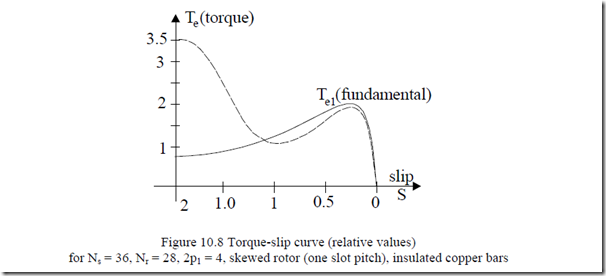
Finally these discrepancies between theory and practice occur even for insulated copper bar cage rotors where the transverse (lamination) rotor currents cannot occur (Figure 10.8).

What may cause such a large departure of experiments from theory? Although a general, simple, answer to this question is still not available, it seems intuitive to assume that the airgap magnetic conductance harmonics due to slot openings and the tooth head saturation due leakage path saturation are the main causes of spectacular braking torque augmentation and notable reduction high slip motoring torque in.

This is true when the contact resistance of rotor bars (practically insulated rotor bars) is high and, thus, the transverse (lamination) currents in skewed rotors are small.

Slot openings have been shown to increase considerably the parasitic torques. (Remember we showed earlier in this chapter that the first slot (step) stator mmf harmonic ν_smin ^{= N}_p1^s −1 is amplified by the influence of the first

airgap magnetic conductance–due to slot openings – (10.33)).

Now the leakage path saturation produced airgap magnetic conductance (10.11) may add further to amplify the parasitic torques.

For skewed rotors, at high slips, where parasitic torques occur, main path flux saturation due to the uncompensated (skewing) rotor mmf may lead to a fundamental torque increase in the braking region (due to higher current, for lower leakage inductance) and to the amplification of parasitic torque through main path saturation-caused airgap conductance harmonics (10.20). And, finally, rotor eccentricity may introduce its input to this braking torque escalation.

escalation.

We have to stress again that leakage flux path saturation and skin effects alone, also cause important increases in rotor resistance, decreases in motor reactance, and thus produce also more fundamental torque.

In fact, the extreme case on Figure 10.8 with a steady increase of torque with slip (for S > 1) seems to be a mixture of such intricated contributions. However, the minimum torque around zero speed shows the importance of parasitic torques as the skin effect and leakage saturation depend on S ; so they change slower with slip than Figure 10.7 suggests.

10.9.6. A case study: N_s/N_r = 36/28, 2p₁ = 4, y/τ = 1 and 7/9; m = 3 [7] As there is no general answer, we will summarize the case of a three-phase induction motor with P_n = 11 kW, N_s/N_r = 36/28, 2p₁ = 4, y/τ = 9/9 and 7/9 (skewed rotor by one stator slot pitch).

For this machine, and y/τ = 9/9, with straight slots, condition (10.71) is not satisfied as

N_r = 28 = 2p 3c₁( m1)= 2 2 3⋅ ( c +1); for c = 2 (10.86)

This means that a synchronous torque occurs at the speed

n = ^4f1 = ^{4⋅50 60⋅} = 215rpm (10.87) N_r 28

Other synchronous, but smaller, torques may be detected. A very large synchronous torque has been measured at this speed (more than 14 Nm, larger than the peak torque for 27% voltage). This leads to a negative total torque at 215 rpm; successful acceleration to full speed is not always guaranteed. It is also shown that as the voltage increases and saturation takes place, the synchronous torque does not increase significantly over this value.

Also, a motor of 70 kW, N_s/N_r = 48/42, y/τ = 10/12 with ∆ connection and 4 parallel current paths has been investigated. As expected, a strong synchronous torque has been spotted at standstill because condition (10.65) is not met as

N_r 6 (10.88)

The synchronous torque at stall is amplified by ∆ connection with 4 paths in parallel stator winding as N_s – N_r = 48 – 42 = 6 = 3p₁ = 3⋅2.

The situation is so severe that, for 44% voltage and 30% load torque, the motor remains blocked at zero speed.

Strong variations of motor torque with position have been measured and calculated satisfactorily with the finite difference method. Saturation consideration seems mandatory for realistic torque calculations during starting transients.

It has also been shown that the amplification of parasitic torque due to slot openings is higher for N_r > N_s because the differential leakage coefficient ^τ_{d } Ns±1 is smaller in this case, allowing for large rotor mmf harmonics. From

 p1 

the point of view of parasitic torques, the rotor with N_r < N_s is recommended and may be used without skewing for series-connected stator windings. For N_r > N_s skewing is recommended unless magnetic wedges in the stator slots are used.

10.9.7. Evaluation of parasitic torques by tests (after [1])

To assist potential designers of IMs, here is a characterization of torque/speed curve for quite a few stator /rotor slot numbers of practical interest. For N_s = 24 stator slots, f₁ = 50 Hz, 2p₁ = 4

• N_r = 10; small synchronous torques at n = 150, 300, 600 rpm and a large one at n = −300 rpm

• N_r = 16; unsuitable (high synchronous torque at n = 375 rpm)

• N_r = 18; very suitable (low asynchronous torque dips at n = 155 rpm and at –137 rpm)

• N_r = 19; unsuitable because of high noise, although only small asynchronous torque dips occur at n = 155 rpm and n = −137 rpm

• N_r = 20; greatest synchronous torque of all situations investigated here at n = −300 rpm, unsuitable for reversible operation.

• N_r = 22; slight synchronous torques at n = 690, 600, ±550, 214, -136 rpm

• N_r = 24; unsuitable because of high synchronous torque at n = 0 rpm

• N_r = 26; larger asynchronous torque deeps at n = 115, −136 rpm and synchronous one at n = -300 rpm • N_r = 27; high noise

• N_r = 28; high synchronous torque dip at n = 214 rpm and slight torque dips at n = 60, −300, −430 rpm. Asynchronous torque dips at n = 115, −136 rpm. With skewing, the situation gets better, but at the expense of 20% reduction in fundamental torque.

• N_r = 30; typical asynchronous torque dips at n = 115, −136 rpm, small synchronous ones at n = 600, ±400, ±300, 214, ±200, −65, −100, −128 rpm. Practically noiseless.

• N_r = 31; very noisy.

Number of slots N_s = 36, f₁ = 50Hz, 2p₁ = 4

This time, the asynchronous torques are small. At n = 79 to 90 rpm, they become noticeable for higher number of rotor slots (44, 48).

• N_r = 16; large synchronous torque at n = −188, +376 rpm

• N_r = 20; synchronous torque at n = −376 rpm

• N_r = 24; large synchronous torque at n = 0 rpm, impractical

• N_r = 28; large synchronous torque at n = −214 rpm, −150, −430 rpm

• N_r = 31; good torque curve but very noisy

• N_r = 32; large synchronous torque at n = −188 rpm and a smaller one at n = −375 rpm;

• N_r = 36; impractical, motor locks at zero speed;

• N_r = 44; large synchronous torque at n = −136 rpm, smaller ones at n = 275, −40, −300 rpm

• N_r = 48; moderate synchronous torque dip at zero speed

Number of slots N_s = 48, f₁ = 50 Hz, 2p₁ = 4

• N_r = 16; large synchronous torque at n = −375, a smaller one at n=-188 rpm

• N_r = 20; large synchronous torque at n = −300 rpm, small ones at n = 600, 375, 150, 60, −65, −136, −700 rpm

• N_r = 22; large synchronous torque dip at n = −136 rpm due to the second rotor slip harmonic (c₂ = 2, n ⁼ c N^{2f1 = −2}2^{⋅50 60}_⋅22^⋅ = −136 rpm )

2 r

• N_r = 28; high synchronous torque at n = 214 rpm, smaller ones at n = 375, 150, −65, −105, -136, −214rpm

• N_r = 32; high synchronous torque at n = −188 rpm, small ones at n = 375, 188, −90, 90, −300 rpm

• N_r = 36; large torque dip at zero speed, not good start

• N_r = 44; very large synchronous torque at n = −136 rpm, smaller ones at n = 275, 214, 60, −300 rpm

• N_r = 48; motor locks at zero speed (N_s = N_r = 48!), after warming up, however, it starts!

10.10. RADIAL FORCES AND ELECTROMAGNETIC NOISE

Tangential forces in IMs are producing torques which smoothly drive the IM (or cause torsional vibrations) while radial forces are causing vibration and noise.

This kind of vibration and noise is produced by electromagnetic forces which vary along the rotor periphery and with time. Using Maxwell tensor, after neglecting the tangential field component in the airgap (as it is much lower than the radial one), the radial stress on the stator is

pr = B22(θµm0 ,t); θ = θmp1 (10.89)

where B(θ,t) is the resultant airgap flux density.

The expression of B(θ_m,t) is, as derived earlier in this chapter,

B(θ_m ,t)^{= µ}_g⁰ (F₁(θ_m ,t)+ F₂ (θ_m ,t))⋅λ θ( _m ,t) (10.90)

with F₁(θ_m,t) and F₂(θ_m,t) the stator and rotor mmf and λ(θ_m,t) the airgap magnetic conductance as influenced by stator and rotor slot openings, leakage, and main path saturation and eccentricity.

∞ ∞   ωr t   (10.91)

F₁(θ_m ,t)= ∑F₁ν cos(νθ_m ± ω_νt) (10.92)

F2 (θm ,t)= ∑F2µ cos(µθm ± ωµt + ϕµ) (10.93)

In (10.89 through 10.93) we have used the mechanical angle θm as the permeance harmonics are directly related to it, and not the electrical angle θ = p1θm. Consequently, now the fundamental, with p1 pole pairs, will be ν1 = p1 and not ν = 1.

Making use of (10.92 and 10.93) in (10.89) we obtain terms of the form

pr = A cosr (γθm − Ωr t) (10.94)

Ωr , which is not be γ = 0,1,2,…. The frequency of these forces is fr = 2p1

confused to the rotor speed ωr/p1.

If the number of pole pairs (γ) is small, stator vibrations may occur due to such forces. As inferred from (10.90), there are terms from same harmonic squared and interaction terms where 1(2) mmf harmonics interact with an airgap magnetic conductance. Such combinations are likely to yield low orders for γ. For γ = 0, the stress does not vary along rotor periphery but varies in time producing variable radial pressure on the stator (and rotor).

For γ = 1 (10.94) yields a single-sided pull on the rotor which circulates with the angular velocity of Ωr. If Ωr corresponds to a mechanical resonance of the machine, notable vibration will occur.

Case γ = 1 results from the interaction of two mechanical harmonics whose order differs by unity.

For γ = 2, 3, 4, … stator deflections occur. In general, all terms pr with γ ≤ 4 should be avoided, by adequately choosing the stator and rotor slot number pairs

Ns and Nr.

However, as mechanical resonance of stators (without and with frames attached) decreases with motor power increase, it means that a certain Ns, Nr combination may lead to low noise in low power motors but to larger noise in large power motors.

Now as in (10.90), the mmf step harmonics and the airgap magnetic conductance occur, we will treat their influence separately to yield some favourable Ns, Nr combinations.

10.10.1. Constant airgap (no slotting, no eccentricity)

In this case λ(θm,t) = λ0 and a typical pr term occurs from two different stator and rotor mmf harmonics.

( )pr γ=ν−µ = µ02F F1gν2 2µ λ02 cos[(γ m µ θ) m ± ω + ω( ν µ)− ϕµ] (10.95)

In this case γ = ν – µ, that is the difference between stator and rotor mmf mechanical harmonics order.

Now if we are considering the first slot (step) mmf harmonics ν, µ,

ν = Ns ± p1 (10.96)

µ = Nr ± p1

It follows that to avoid such forces with γ = 0, 1, 3, 4,

Ns − Nr ≠ 0,1,2,3,4 (10.97)

Ns − Nr ≠ 2p , 2p1 1 ±1, 2p1 ± 2, 2p1 ± 3, 2p1 ± 4

The time variation of all stator space harmonics has the frequency ων = ω1 =

2πf1, while for the rotor,



ω = ωµ 1 m cNrω = ωr 1m c Np1r (1−S)



Notice that ωr is the rotor mechanical speed here.

Consequently the frequency of such forces is ων ± ωµ.

(10.98)



ω = ω ± ω =ξ ν µ  ω1c Np1r N(1−S)



(10.99)

2ω + ω1 1c p1r (1−S)

In general, only frequencies ωξ low enough (c = 1) can cause notable stator vibrations.

The frequency ωξ is twice the power grid frequency or zero at zero speed (S = 1) and increases with speed.

10.10.2. Influence of stator/rotor slot openings, airgap deflection and saturation

As shown earlier in this chapter, the slot openings introduce harmonics in the airgap magnetic conductance which have the same order as the mmf slot (step) harmonics.

Zero order (γ = 0) components in radial stress pr may be obtained when two harmonics of the same order, but different frequency, interact. One springs from the mmf harmonics and one from the airgap magnetic conductance harmonics. To avoid such a situation simply,

NNsr ±± pp11 ≠≠ NNsr or Ns − Nr ≠ ±p1 (10.100)

Also, to avoid first order stresses for γ = 2,

2(Nr − Ns m p1 )≠ 2

(10.101)

Ns − N r ≠± ±p1 1

(10.102)

The frequency of such stresses is still calculated from (10.100) as

ω = ω ± ωξ  1 1 Np1r (1−S 2) (10.103)

The factor 2 above comes from the fact that this stress component comes from a term squared so all the arguments (of space and time) are doubled. It has been shown that airgap deformation itself, due to such forces, may affect the radial stresses of low order.

In the most serious case, the airgap magnetic conductance becomes

λ θ( m ,t)= g ,t

⋅[1+ Bcos K( θm − Ωt)]

The last factor is related to airgap deflection. After decomposition of λ(θm,t) in simple sin(cos) terms for K = p1, strong airgap magnetic conductance terms may interact with the mmf harmonics of orders p1, Ns ± p1, Nr ± p1 again. So we have to have

(Ns ± p1 ) (− Nr ± p1 )≠ p1

or Ns − Nr≠ p1 (10.115)

and Ns − Nr≠ 3p1

In a similar way, slot leakage flux path saturation, already presented earlier in this chapter with its contribution to the airgap magnetic conductance, yields conditions as above to avoid low order radial forces.

10.10.3. Influence of rotor eccentricity on noise

We have shown earlier in this chapter that rotor eccentricity–static and dynamic–introduces a two-pole geometrical harmonics in the airgap magnetic conductance. This leads to a p1 ± 1 order flux density strong components (10.90) in interaction with the mmf fundamentals. These forces vary at twice stator frequency 2f1, which is rather low for resonance conditions. In interaction with another harmonic of same order but different frequency, zero order (γ = 0) vibrations may occur again. Consider the interference with first mmf slot harmonics Ns ± p1, Nr ± p1

(Ns ± p1 ) (− Nr ± p1 )≠ p1 ±1

or Ns − Nr ≠ 3p1 ±1 (10.106)

Ns − Nr ≠ p1 ±1

These criteria, however, have been found earlier in this paragraph. The dynamic eccentricity has been also shown to produce first order forces (γ = 1) from the interaction of p1 ± 1 airgap magnetic conductance harmonic with the fundamental mmf (p1) as their frequencies is different. Noise is thus produced by the dynamic eccentricity.

10.10.4. Parallel stator windings

Parallel path stator windings are used for large power, low voltage machines (now favored in power electronics adjustable drives). As expected, if consecutive poles are making current paths and some magnetic asymmetry occurs, a two-pole geometric harmonic occurs. This harmonic in the airgap magnetic conductance can produce, at least in interaction with the fundamental mmf, radial stresses with the order γ = p1 ± 1 which might cause vibration and noise.

On the contrary, with two parallel paths, if north poles make one path and south poles the other current path, with two layer full pitch windings, no asymmetry will occur. However, in single layer winding, this is not the case and stator harmonics of low order are produced (ν = Ns/2c). They will never lead to low order radial stress, because, in general, Ns and Nr are not far from each other in actual motors.

Parallel windings with chorded double layer windings, however, due to circulating current, lead to additional mmf harmonics and new rules to eliminate noise, [1]

Ns − Nr = p1 ± p ±

a 1 1; a -odd (10.107)

Ns − Nr = 2ap1 ± p1 ±1; a -even

where a is the number of current paths.

Finally, for large power machines, the first slot (step) harmonic order Ns ± p1 is too large so its phase belt harmonics n = (6c1 ± 1)p1 are to be considered in (10.117), [1]

Ns ± pa1 − (6c1 ±1)p1 ≠1; a > 2, odd

2ap1 − (6c1 ±1)p1 ≠1; a > 2, even (10.108)

Nr ± 2p1 − (6c1 ±1)p1 ≠1; a = 2

with c1 a small number c1 = 1,2,….

Symmetric (integer q) chorded windings with parallel paths introduce, due to circulating current, a 2p1 pole mmf harmonic which produces effects that may be avoided by fulfilling (10.108).

10.10.5. Slip-ring induction motors

The mmf harmonics in the rotor mmf are now ν = c2Nr ± p1 only. Also, for integer q2 (the practical case), the number of slots is Nr = 2⋅3⋅p1⋅q2. This time the situation of Ns = Nr is to be avoided; the other conditions are automatically fulfilled due to this constraint on Nr. Using the same rationale as for the cage rotor, the radial stress order, for constant airgap, is

r = ν = µ = (6c1 ±1)p1 − (6c2 ±1)p1 (10.109)

Therefore γ may only be an even number.

Now as soon as eccentricity occurs, the absence of armature reaction leads to higher radial uncompensated forces than the cage rotors. The one for γ = p1 ± 1–that in interaction with the mmf fundamental, which produces a radial force at 2f1 frequency–may be objectionable because it is large (no armature reaction) and produces vibrations anyway.

So far, the radial forces have been analyzed in the absence of magnetic saturation and during steady state. The complexity of this subject makes experiments in this domain mandatory.

Thorough experiments [8] for a few motors with cage and wound rotors confirm the above analysis in general, and reveal the role of magnetic saturation of teeth and yokes in reducing these forces (above 70 to 80% voltage). The radial forces due to eccentricity level off or even decrease.

During steady state, the unbalanced magnetic pull due to eccentricity has been experimentally proved much higher for the wound rotor than for the cage rotor! During starting transients, both are, however, only slightly higher than for the wound rotor under steady state. Parallel windings have been proven to reduce the uncompensated magnetic pull force (γ = 0).

It seems that even with 20% eccentricity, UMP may surpass the cage rotor mass during transients and the wound rotor mass even under steady state. [8]

The effect of radial forces on the IM depends not only on their amplitude and frequency but also on the mechanical resonance frequencies of the stator, so the situation is different for low medium power and large power motors.

10.10.6 Mechanical resonance stator frequencies

The stator ring resonance frequency for r = 0 (first order) radial forces F₀ is [1]

F0 = 8R⋅10a 2 G yokeG yoke+ G teeth (10.110)

with R_a–average stator yoke radius, G_yoke and G_teeth stator yoke and teeth weight. For r ≠ 0,

Fr = F0 2 31 hRyokea r r(r22 −+11)K r (10.111)

h_yoke–yoke radial thickness.

K_r = 1 for h_yoke/R_a > 0.1 and 0.66 < K_r < 1 for h_yoke/R_a < 0.1.

The actual machine has a rather elastic frame fixture to ground and a less than rigid attachment of stator laminations stack to the frame.

This leads to more than one resonance frequency for a given radial force of order r. A rigid framing and fixture will reduce this resonance “multiplication” effect.

To avoid noise, we have to avoid radial force frequencies to be equal to resonance frequencies. For the step harmonics of mmfs contribution (10.100) applies.

for r = 0, at S = 0 (zero slip),

F0 ≠ c Nr or F0 ≠ c Nr ± 2; c =1,2 (10.122)

f1 p1 f1 p1

We may proceed, for r = 1, 2, 3, by using F_r instead of F₀ in (10.112) and with c = 1.

In a similar way, we should proceed for the frequency of other radial forces (derived in previous paragraphs).

In small power machines, such conditions are easy to meet as the stator resonance frequencies are higher than most of radial stress frequencies. So radial forces of small pole pairs r = 0, 1, 2 are to be checked. For large power motors radial forces with r = 3, 4 are more important to account for.

The subject of airgap flux distribution, torque pulsations (or parasitic torques), and radial forces has been approached recently by FEM [9,10] with good results, but at the price of prohibitive computation time.

Consequently, it seems that intuitive studies, based on harmonics analysis, are to be used in the preliminary design study and, once the number of stator/rotor slots are defined, FEM is to be used for precision calculation of parasitic torques and of radial forces.