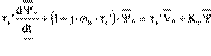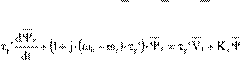ELECTRICAL TRANSIENTS WITH FLUX LINKAGES AS VARIABLES

Equations (13.30) may be transformed by changing the variables through currents elimination.

−1Ψs −Ψr Lm ; σ =1- Lm2

is = σ

 Ls L Ls r  L Ls r (13.54)

ir = σ−1Ψr −Ψs Lm   L_r L L_{s r} 

r

(13.55)

s

with

Ks = LLms ; Kr = LLmr

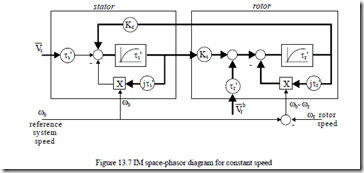
By electrical transients we mean constant speed transients. So both ω_b and ω_r are considered known. The inputs are the two voltage space phasors V_s and V_r and the outputs are the two flux linkage space phasors, Ψ_s and Ψ_r .

The structural diagram of Equations (13.55) is shown in Figure 13.7. The transient behavior of stator and rotor flux linkages as complex variables, at constant speed ω_b and ω_r, for standard step or sinusoidal voltages

V_s , V_r signals has analytical solutions. Finally, the torque transients also have analytical solutions as

The two complex eigenvalues of (13.55) are obtained from

τs ‘p+ + ω τ−1Ksj b s ‘ τr ‘p+ +1 −j(Kω −ω τrb r ) r’ = 0 (13.58)

As expected, the eigenvalues p_1,2 depend on the speed of the motor and on the speed of the reference system ω_b. Equation (13.58) may be put in the form

+p2(τ τ +1s+’ jr⋅ω ⋅τ’ pb[(τ +τss” 1r ‘)+ τ τj s ‘ r ‘ 2( ω −ωb r )]−K Ks r + (13.58’) )( + j⋅ ω −ω ⋅τ( b r ) r ‘)= 0

In essence, in-rush current and torque (at zero speed), for example, has a rather straightforward solution through the knowledge of eigenvalues, with ω_r = 0 = ω_b.

p²τ τ + τ +τ −_s ‘ _r ‘ p( _s ‘ _r ‘) K K_{s r} + =1 0

(p_1,2 )ω =ω =r b ₀ = − τ +τ( _s ‘ _r ‘)± (τ +τ_s ^‘ _{2rτ τ}‘⁾_s²_‘ − τ τ_{r ‘}4 _s ‘ _r ‘(−K K_{s r} +1⁾ (13.59)

The same capability of yielding analytical solutions for transients is claimed by the spiral vector theory. [5]

For constant amplitude stator or rotor flux conditions

^_ ^d_dt^Ψs = j(ω −ω Ψ_{1 b} ) _s or ^d_dt^Ψr = j(ω −ω Ψ_{1 b} ) _r ; ω −₁ stator frequency^_

Equations (13.55) are left with only one complex eigenvalue. Even a simpler analytical solution for electrical transients is feasible for constant stator and rotor flux conditions, so typical in fast response modern vector control drives. Also, at least at zero speed, the eigenvalue with voltage supply is about the same for stator or for rotor supply.

The same equations may be expressed with is and Ψ_r as variables, by simply putting a = L_m/L_r and by eliminating ir from (13.51) with (13.50).

INCLUDING MAGNETIC SATURATION IN THE SPACE PHASOR MODEL

To incorporate magnetic saturation easily into the space phasor model (13.49), we separate the leakage saturation from main flux path saturation with pertinent functions obtained a priori from tests or from field solutions (FEM).

L_sl = L_sl (i , Ls ) _lr = L_lr (i ; r ) Ψ_m = L_m (im ) im (13.60)

im = is +ir (13.61)

Let us consider the reference system oriented along the main flux Ψ_m , that is, Ψ_m = Ψ_m , and eliminate the rotor current, maintaining Ψ_m and is as variables.

V_s = [R_s +(p + ωj _b )L_sl (is )]⋅is +(p+ ωj _b )⋅Ψ_m

[ ( )] ( ) (13.62)

Vr = R_r +(p + j(ω −ω_{b r} ))L_lr im −is ⋅ im −is +(p + j(ω −ω_{b r} ))⋅Ψ_m

Ψ^m (13.63) i_m = _Lm _{( )i}m

We may add the equation of motion,

JpPω₁ r = 23 p Real j1 ( Ψmis* )−Tload (13.64)

Provided the magnetization curves L_sl(i_s), L_lr(i_r) are known, Equations (13.62)–(13.64) may be solved only by numerical methods after splitting Equations (13.62) along d and q axis.

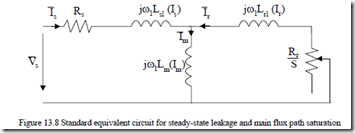
For steady-state, however, it suffices that in the equivalent circuits, Lm is made a function of i_m, L_sl of i_s0 and L_lr(i_ro) (Figure 13.8). This is only in synchronous coordinates where steady-state means dc variables.

In reality, both in the stator and rotor, the magnetic fields are a.c. at frequency ω₁ and Sω₁. So, in fact, in Figure 13.8, the transient (a.c.), inductances should be used.

Llst ( )is = Lls( )is + ∂∂Lisls is < Lls( )is

Llrt ( )ir = Llr ( )ir + ∂∂Lirlr ir < Llr ( )ir (13.65)

Lmt ( )im = Lm ( )im + ∂∂Limm im < Lm ( )im

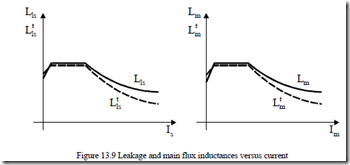
Typical curves are shown in Figure 13.9.

As the transient (a.c.) inductances are even smaller than the normal (d.c.) inductances, the machine behavior at high currents is expected to show further increased currents.

Furthermore, as shown in Chapter 6, the leakage flux circumferential flux lines at high currents influence the main (radial) flux and contribute to the resultant flux in the machine core. The saturation in the stator is given by the stator flux Ψ_s and in the rotor by the rotor flux for high levels of currents.

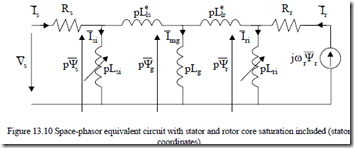
So, for large currents, it seems more appropriate to use the equivalent circuit with stator and rotor flux shown (Figure 13.10). However, two new variable inductances, L_si and L_ri, are added. L_g refers only to the airgap only. Finally the stator and rotor leakage inductances are related only to end connections and slot volume: L_ls^e, L_lr^e. [6]

As expected, the functions Ψ_s(i_si) = L_sii_si and Ψ_r(i_ri) = L_rii_ri have to be known together with L_ls^e, L_lr^e, R_s, R_r, L_g which are hereby considered constant. In the presence of skin effect, L_lr^e and R_r are functions of slip frequency ω_sr = ω₁ – ω_r. Furthermore we should notice that it is not easy to measure all parameters in the equivalent circuit on Figure 13.10. It is, however, possible to calculate them either by sophisticated analytical or through FEM models. Depending on the machine design and load, the relative importance of the two variable inductances L_si and L_ri may be notable or negligible.

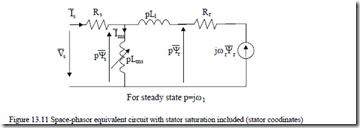
Consequently, the equivalent circuit may be simplified. For example, for heavy loads the rotor saturation may be ignored and thus only L_si remains. Then L_si and L_g in parallel may be lumped into an equivalent variable inductance L_ms and L_ls^e and L_lr^e into the total constant leakage inductance of the machine L_l. Then the equivalent circuit of Figure 13.10 degenerates into the one of Figure 13.11.

When high currents occur, during transients in electric drives, the equivalent circuit of Figure 13.11 indicates severe saturation while the conventional circuit (Figure 13.8) indicates moderate saturation of the main path flux and some saturation of the stator leakage path.

So when high current (torque) transients occur, the real machine, due to the L_ms reduction, produces torque performance quite different from the predictions by the conventional equivalent circuit (Figure 13.8), up to 2 to 2.5 p.u. current, however, the differences between the two models are negligible.

In IMs designed for extreme saturation conditions (minimum weight), models like that in Figure 13.10 have to be used, unless FEM is applied.