LEAKAGE SATURATION AND SKIN EFFECTS–A COMPREHENSIVE ANALYTICAL APPROACH

Magnetic saturation in induction machines occurs in the main path, at low slip frequencies and moderate currents unless closed rotor slots are used when their iron bridges saturate the leakage path.

In contrast, for high slip frequencies and high currents, the leakage flux paths saturate as the main flux decreases with slip frequency for constant stator voltage and frequency.

The presence of slot openings, slot skewing, and winding distribution in slots, make the problem of accounting for magnetic saturation, in presence of rotor skin effects, when the induction machine is voltage fed, a very difficult task.

Ultimately a 3D finite element approach would solve the problem, but for prohibitive computation time.

Less computation, intensive, analytical solutions have been gradually introduced [9−15]. However, only the starting conditions have been treated (with I_s = I_r′ known), with skin effect neglected. Main flux path saturation level, skewing, zig-zag leakage flux have all to be considered for a more precise assessment of induction motor parameters for large currents.

In what follows, an attempt is made to allow for magnetic saturation in the main and leakage path (with skin effect accounted for by appropriate correction coefficients K_R, K_x) for given slip, frequency, voltage, motor geometry, no-load curve, by iteratively recalculating the stator magnetization and rotor currents until sufficient convergence is obtained. So, in fact, the saturation and skin effects are explored from no-load to motor stall conditions.

The computation algorithm presupposes that the motor geometry and the no-load curve as L_m(I_m), magnetising inductance versus no-load current, is known based on analytical or FEM modeling or from experiments.

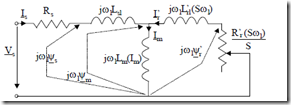
I_s R_s j Lω_{1 sl} I’ j L’ω_{1 rl}(S ω₁)

Figure 9.23 Equivalent circuit with main flux path saturation and skin effects accounted for

The leakage inductances are initially considered unsaturated (as derived in Chapter 6) with their standard expressions. The influence of skin effect on slot– body specific geometric permeance and on resistances is already accounted for in these parameters.

Consequently, given the slip value, the equivalent circuit with the variable parameter L_m(I_m), Figure 9.23, may be solved.

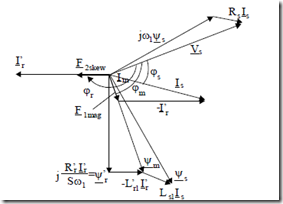
The phasor diagram corresponding to the equivalent circuit in Figure 9.23 is shown in Figure 9.24.

From the equivalent circuit, after a few iterations, based on the L_m(I_m) saturation function, we can calculate I_s, ϕ_s, I_r′, ϕ_r, I_m, ϕ_m.

As expected, at higher slip frequency (Sω₁) and high currents, the main flux ψ_m decreases for constant voltage V_s and stator frequency ω₁. At start (S = 1, rated voltage and frequency), due to the large voltage drop over (R_s + j ω₁L_sl), the main flux Ψ_m decreases to 50 to 60% of its value at no-load.

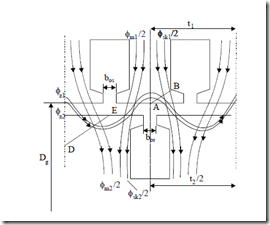
This ψ_m decreasing with slip and current rise led to the idea of neglecting the main flux saturation level when leakage flux path saturation was approached. However, at a more intrusive view, in the teeth top main flux (Ψ_m), slot neck leakage flux (Φ_st1, Φ_st2), zig-zag leakage flux (Φ_z1, Φ_z2), the so-called skewing flux (Φ_sk1, Φ_sk2), and the differential leakage flux (Φ_d1, Φ_d2) all meet to produce the resultant flux and saturation level (Figure 9.25). It is true that these fluxes have, at a certain point of time, their maxima at different positions along rotor periphery.

In essence, the main flux phase angle is ϕ_m , while Φ_st1, Φ_z1, Φ_d1, Φ_st2, Φ_z2, Φ_d2, have the phase angles ϕ_s, ϕ_r, while Φ_sk1, Φ_sk2 are related to rotor current uncompensated mmf and thus is linked to ϕ_r again. As slip varies, not only I_s, I_r′, I_m vary but also their phase angles: especially ϕ_s and ϕ_r′ with ϕ_m about the same. The differential leakage fluxes (Φ_d1, Φ_d2) are not shown in Figure 9.25 though they also act within airgap and teeth top zones, AB and DE.

To make the problem easy and amenable to computation, it is assumed that when saturation occurs in some part of the machine, the ratios between various flux contributions to total flux remain as they were before saturation.

The case of closed rotor slots is to be treated separately. Let us now define the initial expressions of various fluxes per tooth and their geometrical specific leakage permeances.

 

In a similar manner, the zig-zag fluxes Φ_z1 and Φ_z2 are

Φz1 = AT1µ0lstackλz1

Φz2 = AT2µ0lstackλz2 (9.59)

AT₁ = n I_{s s} 2; AT₂ = n I’_{r r} 2; From (9.56) and (9.59) n_r is

nr = I’I= n Ks w1 NNsr (9.60)

The unsaturated zig-zag specific permeances λz1 and λz2 are [5]
K 2 λz1 = 12w1N gπsDg (1.2a1 − 0.2)	(9.61)
K 2 λz2 = 12w1N gπrDg (1.2a2 − 0.2)	(9.62)
a1 = t 5g1( (+ b+os )− b) or2	(9.63)

t 5g1 bos

a 2 = t2 5tg2 (5gbor+ borb)os The slot neck fluxes Φst1 and Φst2 are straightforward.

(9.64)

The differential leakage, specific permeance λ_d1,2 may be derived from a comparison between magnetization harmonic inductances L_mν and the leakage inductance expressions L_sl and L_rl′ (Chapter 7).

Lmν = 6π20 (p1/ν)gK 1lstackc ( W K+1Ksteethwν )	(9.67)
Lsl = 2µ0 Wp q112 (λss + λz1 + λendcon1 + λst1 + λd1)	(9.68)
Lsr = 2µ0 Wp q112 (λsr + λz2 + λendcon2 + λd2 + λst2 + λsk2 )	(9.69)

µ (τ ν) ( )2

λ = ∑∞ K ν2

 1  1 λd2 = λm1 Ns (τd2 − ∆τd2 ); ∆τd2 = Kz2 2p1 2

(9.70)

τd1 = π2 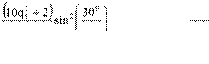27 q −1; ∆τd1 = Kz1 91q2

Nr  Nr 

 πp1 ² 



τd2 =  N_rπp₁  sin π₂p1πN⋅pskew_1rN⋅skew_r ²  −1

sin₂ N_r  

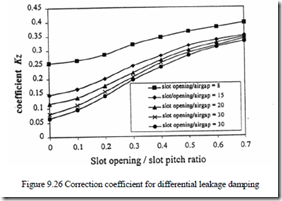
The coefficient K_z1 and K_z2 are found from Figure 9.26.

The slot-specific geometric permeances λ_ss and λ_sr, for rectangular slots, with rotor skin effect, are

λss = 3hbss + λst1 (9.71)

λ_sr = 3^hb^rr ⋅K_X + λ_st2; K_x −skin effect correction (9.72)

The most important “ingredient” in leakage inductance saturation is, for large values of stator and rotor currents, the skewing (uncompensated) mmf.

9.7.1. The skewing mmf

The rotor (stator) slot skewing, performed to reduce the first slot harmonic torque (in general) has also some side effects such as: a slight reduction in the magnetization inductance L_m accompanied by an additional leakage inductance component, L′_rskew. We decide to “attach” this new leakage inductance to the rotor as it “disappears” at zero rotor current

 

 

To account for L_m alteration due to skewing, we use the standard skewing factor Kskewconv .

sin^ ^π2 skew / m q_{1 1} ^ ; Kskewconv ≈ 0.98−1.0 (9.73)

Kskewconv =  skew / m q_{1 1}

and include a rotor current linear dependence to make sure that the influence disappears at zero rotor current,

Kskew =1− (1− Kskewconv )I ‘Irs (9.74)

skew–is the skewing in stator slot pitch counts.

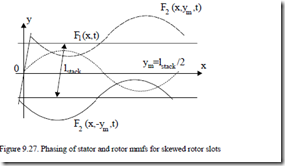
To account for the skewing effect, we first consider the stator and rotor mmf fundamentals for a skewed rotor.

As the current in the bar is the same all along the stack length (with interbar currents neglected), the rotor mmf phasing varies along OY, beside OX and time (Figure 9.27) so the resulting mmf fundamental is

+ F2m sin πτ x − π2 f t1 − ϕ − ϕ( s r )− m qπ1 1 skew lstacky  (9.75)



− lstack ≤ y ≤ lstack

2 2

We may consider this as made of two terms, the magnetization mmf F_1mag and the skewing mmf F_2skew.

F x,y,t( )= F1mag + F2skew (9.76)

F1mag = F1m sin πτ x − π2 f t1  +

+ F₂  π skew y ⋅sin πτ x − π2 f t1 − ϕ − ϕ( s r ) (9.77) m cos m q1 1 lstack 



 π y ⋅cos πτ x − π2 f t1 − ϕ − ϕ( s r ) (9.78) F2skew = −F2m sin m q1 1 skew lstack  

F_1mag is only slightly influenced by skewing (9.77) as also reflected in (9.73).

On the other hand, the skewing (uncompensated) mmf varies with rotor current (F_2m) and with the axial position y. It tends to be small even at rated current in amplitude (9.78) but it gets rather high at large rotor currents. Notice also that the phase angle of F_1mag (ϕ_m) and F_2skew (ϕ_r) are different by slightly more than 90⁰ (Figure 9.24), above rated current,

ϕ_skew = ϕ − ϕ_{r m} (9.79)

We may now define a skewing magnetization current I_mskew:

Imskew = ±Im ATAT12m sin(π2p SKW / N1 1 s ) (9.80)

Example 9.6. The skewing mmf

Let us consider an induction motor with the following data: no-load rated current: I_m = 30% of rated current; starting current. 600% of rated current; the number of poles: 2p₁ = 4, skew = 1 stator slot pitch; number of stator slots N_s =

36. Assessment of the maximum skewing magnetization current I_mskew/I_m for starting conditions is required.

Solution

Making use of (9.80), the skewing magnetization current for SKW₁ = ±skew.

ImskewIm = ± ATAT12m sin π2p skew /1⁽N_s 2) = ± II ‘_mr sin π⋅4 136⋅ / 2  ≈

≈ ± IIstartm ⋅0.15643 = ± 60030%% ⋅0.15643 = ±3.1286! 

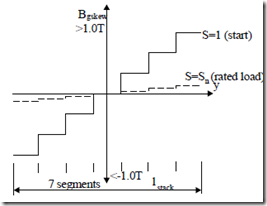
This shows that, at start, the maximum flux density in the airgap produced by the skewing magnetization current in the extreme axial segments will be maximum and much higher than the main flux density in the airgap, which is dominant below rated current when I_mskew becomes negligible (Figure 9.28).

 

Figure 9.28 Skewing magnetization current produced airgap flux density

Airgap flux densities in excess of 1.0 T are to be expected at start and thus heavy saturation all over magnetic circuit should occur.

Let us remember that in these conditions the magnetization current is reduced such that the airgap flux density of main flux is (0.6 – 0.65) of its rated value, and its maximum is phase shifted with respect to the skewing flux by more than 90⁰ (Figure 9.24). Consequently at start (high currents), the total airgap flux density is dominated by the skewing mmf contribution! This phenomenon has been documented recently through FEM [16]. Dividing the stator stack in (N_seg + 1) axial segments, we have:

SKW₁ = 0.0, ^skewNseg , ^skew2 (9.81)

Now, based on I_mskew, from the magnetization curve (L_m(I_m)), we may calculate the magnetization inductance for skewing magnetization current L_m(I_mskew). Finally we may define a specific geometric permeance for skewing λ_sk1.

λsk1 = N Ks Lw1mW n(I1mskewsµ0)lstack (9.82)

W₁–turns/phase. λ_sk1 depends on the segment considered (6 to 10 segments are enough) and on the level of rotor current.

Now the skewing flux/tooth in the stator and rotor is

Φsk1 = AT sin2  2p SKW1Ns 1µ0lstackλsk1 	(9.83)
Φsk2 = Φsk1 Ns	(9.84)

 π 

Nr

In (9.83), the value of Φ_sk1 is calculated as if the value of segmented skewing is valid all along the stack length. This means that all calculations will be made n_seg times and then average values will be used to calculate the final values of leakage inductances.

Now if the skewing flux occurs both in the stator and in the rotor, when the leakage inductance is calculated, the rotor one will include the skewing permeance λ_sk2.

λsk2 = λsk1 NNsr (9.85)

9.7.2. Flux in the cross section marked by AB (Figure 9.25)

The total flux through AB, Φ_AB is

Φ_AB = Φ2m1 + ^Φ2sk1 + Φ_z1 + Φ_z2 + Φ_st1 (9.86)

Let us denote

Cm1 = ₂Φ_Φ^m1_AB Csk1 = ₂^Φ_Φ^sk1_AB Cz1 = _Φ^Φ_AB^z1 (9.87)

Φ^st1 Cz2 = _Φ^Φ_AB^z2 (9.88)

Cst1 = _ΦAB

These ratios, calculated before slot neck saturation is considered, are also taken as valid for a total leakage saturation condition.

There are two different situations: one with the stator tooth saturating first and the second with the saturated rotor teeth.

9.7.3. The stator tooth top saturates first

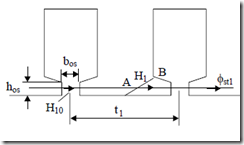
Making use of Ampere’s and flux laws, the slot neck zone is considered (Figure 9.29).

 

(t1 − bos )H1 + b Hos 10 = AT1 The total flux through AB is	(9.89)
ΦABsat = AB l⋅ stack ⋅B1	(9.90)

On the other end, with C_st1 known from unsaturated conditions, the slot neck flux Φ_st1 is

Φst1 = Cst1ΦABsat = µ0H h l10 os stack From (9.89) – (9.91), we finally obtain	(9.91)
	AT1 − t ‘H1 1

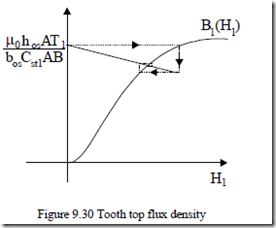
B1 = µ0hos _{b Cos st1AB} ; t ‘1 = t1 − bos (9.92) Equation (9.92) corroborated with the lamination B₁(H₁) magnetization curve leads to B1 and H1 (Figure 9.30).

An iterative procedure as in Figure 9.30 may be used to solve (9.92) for B₁ and H₁. Finally, from (9.90), the saturated value of (Φ_AB)_sat is obtained.

Further on, new values of various teeth flux components are obtained.

 Φ2m1 _sat = Cm1(ΦAB )sat

(Φsk1)sat = Csk1(ΦAB )sat (9.93)

(Φz1)sat = Cz1(ΦAB )sat

(Φst1)sat = Cst1(ΦAB )sat

The new (saturated) values of stator leakage permeance components are

(λz1)sat = AT(Φ11µz100l)satstackstack

(9.94)

(λst1)sat = AT(Φµst1l)sat

The end connection and differential geometrical permeances λ_endcon and λ_d1 maintain, in (9.68), their unsaturated values, while (λ_st1)_sat and (λ_z1)_sat (via (9.94)) enter (9.68) and thus the saturated value of stator leakage inductance L_sl for given stator and rotor currents and slip is obtained.

We have to continue with the rotor. There may be two different situations.

9.7.4. Unsaturated rotor tooth top

In this case the saturation flux from the stator tooth is “translated” into the rotor by the ratio of slot numbers N_s/N_r.

(λst2 )sat = (ATΦst11µ)sat0lstackNNsr

(λz2 )sat = (ATΦz11µ)sat0lstackNNsr (9.95)

(λsk2 )sat = λsk1 NNsr

In Equation (9.95) it is recognised that the skewing flux “saturation” is not much influenced by the tooth top flux zone saturation as it represents a small length flux path in comparison with the main flux path available for skewing flux.

By now, with (9.69), the saturated rotor leakage inductance L_rl′ may be calculated. With these new, saturated, leakage inductances, new stator, magnetization, and rotor currents are calculated.

The process is repeated until sufficient convergence is obtained with respect to the two leakage inductances. A new slip is then chosen and the computation cycle is repeated.

9.7.5. Saturated rotor tooth tip

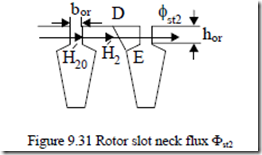
In this case, after the AB zone was explored as above the DE cross section is investigated (Figure 9.31). Again the Ampere’s law across tooth tip and slot neck yields

(t2 − bor )H2 + b Hor 20 = AT2

(9.96)

 

Figure 9.31 Rotor slot neck flux Φst2 The flux law results in
ΦDE = Φ + Φ1 ( st2 )sat ; B2 = µ0H20	(9.97)

where Φ = Φ1 ABsat NNsr (9.98)

Also (Φst2 )sat = DE l⋅ stack ⋅B2 (H2 ); t ‘2 = t2 − bor (9.99)

(Φst2 )sat = µ0H20hos stackl = µ0hor (AT2 b−ort ‘H2 2 )lstack (9.100)

Finally, B2 (H2 )= lstack1DE ΦABsat NNsr + µ0hor (AT2 b−ort ‘H2 2 )lstack  (9.101)

Equation (9.101), together with the rotor lamination magnetization curve, B₂(H₂), is solved iteratively (as illustrated in Figure 9.30 for the stator).

Then,

(λst2 )sat = (Φst2Φ)st2sat λst2 ; λst2 = hboror (9.102)

Φst2 = µ0AT l2 stackλst2 (9.103)

The other specific geometrical permeances in the rotor leakage inductance (λ_z2)_sat and (λ_sk2)_sat are calculated as in (9.95). Now we calculate the saturated value of L_rl′ in (9.69). Then, from the equivalent circuit, new values of currents are calculated and a new iteration is initiated until sufficient convergence is reached.

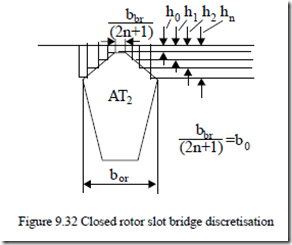
9.7.6. The case of closed rotor slots

Closed rotor slots (Figure 9.32) are used to reduce starting current, noise, vibration, and windage friction losses though the breakdown and starting torque are smaller and so is the rated power factor.

The slot iron bridge region is discretized in 2n + 1 zones of constant (but distinct) permeability µ_j. A value of n = (4 – 6) suffices. The Ampere’s and flux laws for this region provide the following equations:

 n  b₀_H₀ + 2∑H _j _ = AT₂ (9.104)

 1 

B h_{0 0} = B h_{1 1} = B h_{2 2} =K= B h_{n n} (9.105)

Given an initial value for B₀, for given AT₂, B₁, …, B_n are determined from (9.105). From the lamination magnetization curve, H₀, H₁, …, H_n are found. A new value of AT₂ is calculated, then compared with the given one and a new B₀ is chosen. The iteration cycle is revisited until sufficient convergence is obtained.

Finally, the slot bridge geometrical specific permeance (λ_st2)_sat is

(λst2 )sat = hb0₀ B0 + 2b0 B11 +K+ 2hbn0 µB0Hn n (9.106) µ0H0 h1 µ0H1

All the other permeances are calculated as in previous paragraphs.

9.7.7. The algorithm

The algorithm for the computation of permeance in the presence of magnetic saturation and skin effects, as unfolded gradually so far, can be synthesized as following:

• Load initial data (geometry, winding data, name-plate data etc.)

• Load magnetization file: B(H)

• Load magnetization inductance function L_m(I_m) – from FEM, design or tests

• Compute differential leakage specific permeances

• for S = Smin, Sstep, Smax for SKW₁ = 0:skew/n_seg:skew compute unsaturated specific permeances while magnetization current error < 2%

compute induction motor model using nonlinear L_m(I_m) function end;

Save unsaturated parameters 1. if case = closed rotor slots;

compute closed rotor case; else

while H₁ error < 2%; compute stator saturation case; end;

compute unsaturated rotor case;

if case = saturated rotor; while H₂ error < 2%; compute saturated rotor case

end; end.

Compute saturated parameters; compare them with those of previous cycle and go to 1. Return to 1 until sufficient convergence in L_sl and L_rl′ is reached. end.

end (axial segments cycle)

end (slip cycle)

Save saturated parameters for SKW1 = 0:skew/nseg:skew;

Compute saturated parameters average values; plot the IM parameters (segment number, slip);

Compute IM equivalent circuit using an average value for each parameter (for the n_seg, axial segments);

Compute stator, rotor, magnetization current, torque, power factor versus slip;

Plot the results end.

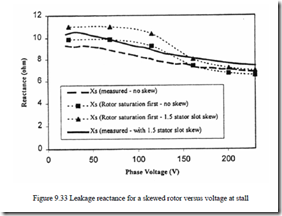
Applying this algorithm for S = 1 an 1.1 kW, 2 pole, three-phase IM with skewed rotor, the results shown on Figure 9.33 have been obtained [18]. Heavy saturation occurs at high voltage level. The model seems to produce satisfactory results.