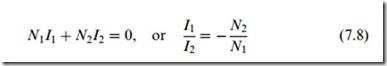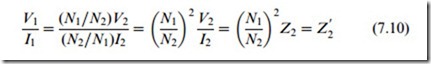THE IDEAL TRANSFORMER
Because we are dealing with balanced 3-phase motors we can achieve considerable simpliWcation by developing single-phase models, it being understood that any calculations using the equivalent circuit (e.g. torque or power) will yield ‘per phase’ values which will be multiplied by three to give the total torque or power.
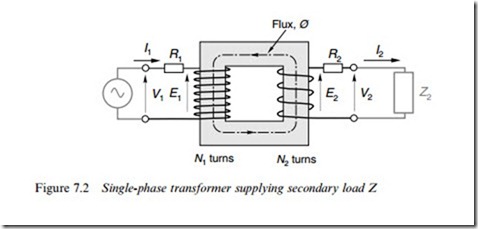
A quasi-circuit model of an iron-cored transformer is shown diagram- matically in Figure 7.2. This represents the most common application of the transformer, with the primary drawing power from an a.c. constant- voltage source (V1) and supplying it to a load impedance (Z2) at a diVerent voltage (V2). (In the real transformer there would not be a big hole in the middle (as in Figure 7.2) because the primary and secondary windings would Wll the space, each winding having the same total volume of copper.)
The primary winding has N1 turns with total resistance R1, and the secondary winding has N2 turns with total resistance R2, and they share a common ‘iron’ magnetic circuit with no air-gap and therefore very low reluctance.
Ideal transformer – no-load condition, flux and magnetising current
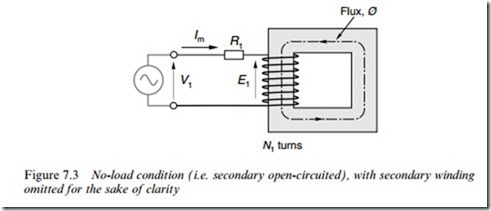
We will begin by asking how the ideal transformer behaves when its primary winding is connected to the voltage source as shown in Figure 7.2, but the secondary is open circuited. This is known as the no-load
condition. Since the secondary has no current it cannot inXuence mat- ters, so we can temporarily remove it to yield the simpler model shown in Figure 7.3. What we want to know is what determines the magnitude of the Xux in the core, and how much current (known for obvious reasons as the magnetising current, Im) will be drawn from the voltage source to set up the Xux.
We apply KirchoV’s voltage law to relate the applied voltage (V1) to the voltage induced in the primary winding by the pulsating Xux (E1) and to the volt-drop across the primary resistance, yielding
We have of course seen similar equations several times before.
We can simplify equation (7.1) further in the case of the ‘ideal’ trans- former, which not unexpectedly is assumed to have windings made of wire with zero resistance, i.e. R1 ¼ 0. So we deduce that for an ideal trans- former, the induced e.m.f. is equal to the applied voltage, i.e. E1 ¼ V1.
This is very important and echoes the discussion in Chapter 5: but what we really want is to Wnd out what the Xux is doing, so we must now use the result that E1 ¼ V1 to recast equation (7.2) in the form
Equation (7.3) shows that the rate of change of Xux at any instant is determined by the applied voltage, so if we want to know how the Xux behaves in time we must specify the nature of the applied voltage. We will look at two cases: the Wrst voltage waveform is good for illustrative purposes because it is easy to derive the Xux waveform, while the second represents the commonplace situation, i.e. use on an supply.
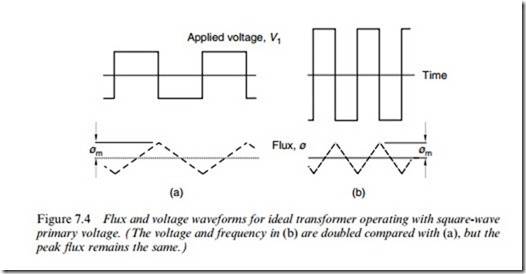
Firstly, we suppose that the applied voltage is a square wave. The rate of change of Xux is positive and constant while V1 is positive, so the Xux increases linearly with time. Conversely, when the applied voltage is negative the Xux ramps down, so the overall voltage and Xux waves are as shown in Figure 7.4(a).
It should be evident from Figure 7.4 that the maximum Xux in the core (wm) is determined not only by the magnitude of the applied voltage (which determines the slope of the Xux/time plot), but also by the frequency (which determines for how long the positive slope continues). Normally we want to utilise the full capacity of the magnetic circuit, so we must adjust the voltage and frequency together to keep wm at its rated value. For example, in Figure 7.4(b) the voltage has been doubled, but so has the frequency, to keep wm the same as in Figure 7.4(a): if we had left the frequency the same, the Xux would have tried to reach twice its rated value, and in the process the core would have become saturated, as explained in Chapter 1.
Turning now to the everyday situation in which the transformer is connected to a sinusoidal voltage given by V1 ¼ V^ sin vt, we can
integrate equation (7.3) to obtain an expression for the Xux. The Xux is then given by
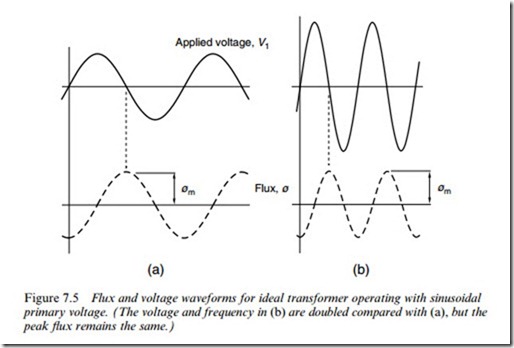
Typical primary voltage and Xux waves are shown in Figure 7.5. A special feature of a sine function is that its diVerential (gradient) is basically the same shape as the function itself, i.e. diVerentiating a sine yields a cosine, which is simply a sine shifted by 908; and similarly, as here, diVerentiating
a (-)cosine wave of Xux yields a sinewave of voltage.
Equation (7.5) shows that the amplitude of the Xux wave is proportional to the applied voltage, and inversely proportional to the frequency. As mentioned above, we normally aim to keep the peak Xux constant in order to fully utilise the magnetic circuit, and this means that changes to voltage or frequency must be done so that the ratio of voltage to frequency is maintained. This is shown in Figure 7.5 where, to keep the peak Xux (wm) in Figure 7.5(a) the same when the frequency is doubled to that in
Figure 7.5(b), the voltage must also be doubled. We drew the same conclusion in relation to the induction motor in Chapters 5 and 6.
Although equation (7.5) was developed for an ideal transformer, it is also applicable with very little error to the real transformer, and is in fact a basic design equation. For example, suppose we have a transformer core with a cross-sectional area 5 cm x 5 cm, and we decide we want to use it as a 240 V, 50 Hz mains transformer. How many turns will be required on the primary winding?
We can assume that, as discussed in Chapter 1, the Xux density in the core will have to be limited to say 1.4 T to avoid saturation. Hence the peak Xux in the core is given by
We cannot have a fraction of a turn, so we choose 309 turns for the primary winding. If we used fewer turns the Xux would be too high, and if we used more, the core would be under-utilised.
The important message to take from this analysis is that under sinusoidal conditions at a Wxed frequency, the Xux in a given transformer is determined by the applied voltage. Interestingly, however, the only assumption we have to make to arrive at this result is that the resistance of the windings is zero: the argument so far is independent of the magnetic circuit, so we must now see how the reluctance of the trans- former core makes its presence felt.
We know that although the amplitude of the Xux waveform is deter- mined by the applied voltage, frequency and turns, there will need to be an MMF (i.e. a current in the primary winding) to drive the Xux around the magnetic circuit: the magnetic Ohm’s law tells us that the MMF required to drive Xux w around a magnetic circuit that has reluctance R is given by MMF ¼ Rw.
But in this section we are studying an ideal transformer, so we can assume that the magnetic circuit is made of inWnitely permeable mater- ial, and therefore has zero reluctance. This means that no MMF is required, so the current drawn from the supply (the ‘magnetising current’, Im) in the ideal transformer is zero.
To sum up, the Xux in the ideal transformer is determined by the applied voltage, and the no-load current is zero. This hypothetical situation is never achieved in practice, but real transformers (especially large ones) come close to it.
Viewed from the supply, the ideal transformer at no-load looks like an open circuit, as it draws no current. We will see later that a real transformer at no-load draws a small current, lagging the applied volt- age by almost 908, and that from the supply viewpoint it therefore has a high inductive reactance, known for obvious reasons as the ‘magnetising reactance’. An ideal transformer is thus seen to have an inWnite magnetising reactance.
Ideal transformer – no-load condition, voltage ratio
We now consider the secondary winding to be restored, but leave it disconnected from the load so that its current is zero, in which case it can clearly have no inXuence on the Xux. Because the magnetic circuit is perfect, none of the Xux set up by the primary winding leaks out, and all of it therefore links the secondary winding. We can therefore apply Faraday’s law and make use of equation (7.3) to obtain the secondary induced e.m.f.
It is worth mentioning that equation (7.7) applies regardless of the nature of the waveform, so if we apply a square wave voltage to the primary, the secondary voltage would also be square wave with amplitude scaled according to equation (7.7).
We will see later that when the transformer supplies a load the primary and secondary currents are inversely proportional to their respective voltages: so if the secondary voltage is lower than the primary there will be fewer secondary turns but the current will be higher and therefore the cross-sectional area of the wire used will be greater. The net result is that the total volumes of copper in primary and secondary are virtually the same, as is to be expected since they both handle the same power.
Ideal transformer on load
We now consider what happens when we connect the secondary winding to a load impedance Z2. We have already seen that the Xux is determined solely by the applied primary voltage, so when current Xows to the load it can have no eVect on the Xux, and hence because the secondary winding resistance is zero, the secondary voltage remains as it was at no-load, given by equation (7.7). (If the voltage were to change when we connected the load we could be forgiven for beginning to doubt the validity of the description ‘ideal’ for such a device!)
The current drawn by the load will be given by I2 = V2=Z2, and the secondary winding will therefore produce an MMF of N2I2 acting around the magnetic circuit. If this MMF went unchecked it would tend to reduce the Xux in the core, but, as we have seen, the Xux is determined by the applied voltage, and cannot change. We have also seen that because the core is made of ideal magnetic material it has no reluctance, and therefore the resultant MMF (due to both the primary winding and the secondary winding) is zero. These two conditions are met by the primary winding drawing a current such that the sum of the primary MMF and the secondary MMF is zero, i.e.
In other words, as soon as the secondary current begins to Xow, a primary current automatically springs up to neutralise the demagnetising eVect of the secondary MMF.
The minus sign in equation (7.8) serves to remind us that primary and secondary MMFs act in opposition. It has no real meaning until we deWne what we mean by the positive direction of winding the turns around the core, so because we are not concerned with transformer manufacture we can aVord to ignore it from now on.
The current ratio in equation (7.8) is seen to be the inverse of the voltage ratio in equation (7.7). We could have obtained the current ratio by a diVerent approach if we had argued from a power basis, by saying that in an ideal transformer, the instantaneous input power and the instantaneous output power must be equal. This would lead us to
conclude that V1I1 ¼ V2I2, and hence from equation (7.7) that
To conclude our look at the ideal transformer, we should ask what the primary winding of an ideal transformer ‘looks like’ when the secondary is connected to a load impedance Z2. As far as the primary supply is concerned, the apparent impedance looking into the primary of the transformer is simply the ratio V1=I1, which can be expressed in secondary terms as
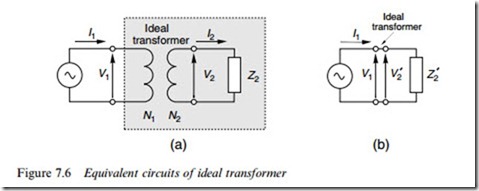
So, when we connect an impedance Z2 to the secondary, it appears from the primary side as if we have connected an impedance Z0 across the primary terminals. This equivalence is summed-up diagrammatically in Figure 7.6.
The ideal transformer eVectively ‘scales’ the voltages by the turns ratio and the currents by the inverse turns ratio, and from the point of view of the input terminals, the ideal transformer and its secondary load (inside the shaded area in Figure 7.6(a)) is indistinguishable from the circuit in Figure 7.6(b), in which the impedance Z 0 (known as the ‘referred’
impedance) is connected across the supply. We should note that when we use referred impedances, the equivalent circuit of the ideal trans- former simply reduces to a link between primary and referred secondary circuits: this point has been stressed by showing the primary and sec- ondary terminals in Figure 7.6, even though there is nothing between them. We will make use of the idea of referring impedance from second- ary to primary when we model the imperfections of the real transformer, and then we will Wnd that there are circuit elements between the input (V1) and output (V 0 ) terminals (Figure 7.10).
Finally, we should note that although both windings of an ideal transformer have inWnite inductance, there is not even a vestige of
inductance in the equivalent circuit. This remarkable result is due to the perfect magnetic coupling between the windings. As we will see shortly, the real transformer can come very close to the ideal, but for reasons that will also become apparent, ultimate perfection is not usually what we seek.