Induction motor:Relation Between Torque and Rotor Power Factor.

Relation Between Torque and Rotor Power Factor

In Art. 29.7, it has been shown that in the case of a d.c. motor, the torque Ta is proportional to the product of armature current and flux per pole i.e. Ta µ f Ia. Similarly, in the case of an induction motor, the torque is also proportional to the product of flux per stator pole and the rotor current. However, there is one more factor that has to be taken into account i.e. the power factor of the rotor.

where k1 is another constant.

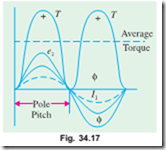
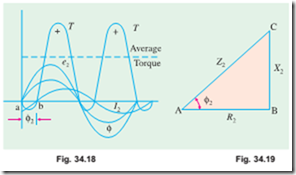
The effect of rotor power factor on rotor torque is illustrated in Fig. 34.17 and Fig. 34.18 for various values of f2. From the above expression for torque, it is clear that as f2 increases (and hence, cos f2 decreases) the torque decreases and vice versa.

In the discussion to follow, the stator flux distribution is assumed sinusoidal. This revolving flux induces in each rotor conductor or bar an e.m.f. whose value depends on the flux density, in which the conductor is lying at the instant considered (: e = Blv volt). Hence, the induced e.m.f. in the rotor is also sinusoidal.

(i) Rotor Assumed Non-inductive (or f2 = 0)

In this case, the rotor current I2 is in phase with the e.m.f. E2 induced in the rotor (Fig. 34.17). The instantaneous value of the torque acting on each rotor conductor is given by the product of instantaneous value of the flux and the rotor current (: F µ BI2l ). Hence, torque curve is obtained by plotting the products of flux f (or flux density B) and I2. It is seen that the torque is always positive i.e. unidirectional.

(ii) Rotor Assumed Inductive

This case is shown in Fig. 34.18. Here, I lags behind E by an angle f = tan-1 rotor resistance/phase; X2 = rotor reactance/phase at standstill.

It is seen that for a portion ‘ab’ of the pole pitch, the torque is negative i.e. reversed. Hence, the total torque which is the difference of the forward and the backward torques, is considerably reduced. If f2 = 90°, then the total torque is zero because in that case the backward and the forward torques become equal and opposite.

Starting Torque

The torque developed by the motor at the instant of starting is called starting torque. In some cases, it is greater than the normal running torque, whereas in some other cases it is somewhat less.

Starting Torque of a Squirrel-cage Motor

The resistance of a squirrel-cage motor is fixed and small as compared to its reactance which is very large especially at the start because at standstill, the frequency of the rotor currents equals the supply frequency. Hence, the starting current I2 of the rotor, though very large in magnitude, lags by a very large angle behind E2, with the result that the starting torque per ampere is very poor. It is roughly 1.5 times the full-load torque, although the starting current is 5 to 7 times the full-load current. Hence, such motors are not useful where the motor has to start against heavy loads.

Starting Torque of a Slip-ring Motor

The starting torque of such a motor is increased by improving its power factor by adding external resistance in the rotor circuit from the star-connected rheostat, the rheostat resistance being progressively cut out as the motor gathers speed. Addition of external resistance, however, increases the rotor impedance and so reduces the rotor current. At first, the effect of improved power factor predominates the current-decreasing effect of impedance. Hence, starting torque is increased. But after a certain point, the effect of increased impedance predominates the effect of improved power factor and so the torque starts decreasing.

Switches, circuit breakers and switchboards:Switches and circuit breakers

Solids, liquids and gases:Timing

Temperature sensing devices:Expansion of Metal

Jogging and inching:Inching Controls

DC Circuits:Wheatstone Bridge

Ohm’s Law:application Of Ohm’s law

The 555 Timer:Circuit Applications

Summary of Certification for the Electricity and Electronics Field

Power Supply Design:Voltage Regulator Systems

TRANSFORMER COMPONENTS AND MAINTENANCE

VARIABLE-VOLTAGE CONTROL

The Operational Amplifier:Basic Circuits