INDUCTION MACHINE TRANSIENTS

INTRODUCTION

Induction machines undergo transients when voltage, current, and (or) speed undergo changes. Turning on or off the power grid leads to starting transients an induction motor.

Reconnecting an induction machine after a short-lived power fault (zero current) is yet another transient. Bus switching for large power induction machines feeding urgent loads also qualifies as large deviation transients.

Sudden short-circuits, at the terminals of large induction motors lead to very large peak currents and torques. On the other hand more and more induction motors are used in variable speed drives with fast electromagnetic and mechanical transients.

So, modeling transients is required for power-grid-fed (constant voltage and frequency) and for PWM converter-fed IM drives control.

Modeling the transients of induction machines may be carried out through circuit models or coupled field/circuit models (through FEM). We will deal first with phase-coordinate abc model with inductance matrix exhibiting terms dependent on rotor position.

Subsequently, the space phasor (d–q) model is derived. Both single and double rotor circuit models are dealt with. Saturation is also included in the space-phasor (d–q) model. The abc–dq model is then derived and applied, as it is adequate for nonsymmetrical voltage supplies and PWM converter-fed IMs. Reduced order d–q models are used to simplify the study of transients for low and large motors, respectively.

Modeling transients with the computation of cage bar and end-ring currents is required when cage and/or end-ring faults occur. Finally the FEM coupled field circuit approach is dealt with.

Autonomous generator transients are left out as they are treated in the chapter dedicated to induction generators. 

THE PHASE COORDINATE MODEL

The induction machine may be viewed as a system of electric and magnetic circuits which are coupled magnetically and/or electrically.

An assembly of resistances, self inductances, and mutual inductances is thus obtained. Let us first deal with the inductance matrix.

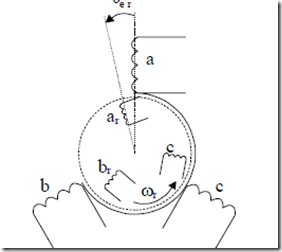
A symmetrical (healthy) cage may be replaced by a wound three-phase rotor. [2] Consequently, the IM is represented by six circuits, (phases) (Figure 14.1). Each of them is characterized by a self inductance and 5 mutual inductances.

The stator and rotor phase self inductances do not depend on rotor position if slot openings are neglected. Also, mutual inductances between stator phases and rotor phases, respectively, do not depend on rotor position. A sinusoidal distribution of windings is assumed. Finally, stator/rotor phase mutual

inductances depend on rotor position (θ_er = p₁θ_r).

 Laa  Lab   [Labca b cr r r (θer )]= LLaaacr Labr  Lacr

Lab Lbb Lbc Lbar Lbbr Lbcr

Lac Lbc Lcc Lcar Lcbr Lccr

Laar Lbar Lcar La ar r La br r La cr r

Labr Lbbr Lcbr La br r Lb br r Lb cr r

The induction matrix, L_{abca b cr r r} (^θ_er )is

LLbcac_rr _

LLa ccc_r r_r  (13.1)

Lb cr r 

Lc cr r 

Figure 13.1 Three-phase IM with equivalent wound rotor

with

Laa = Lbb = Lcc = Lls + Lms; Lab = Lac = Lbc = −Lms /2;

Laar = Lbbr = Lccr = Lsrm cosθer; La ar r = Lb br r = Lc cr r = Lrlr +

Lc ar = La br = Lb cr = Lsrm cosθer − 23π; La br r = La cr r = Lb cr r = −Lrmr /2; (13.2)

Lc br = Lb ar = La cr = Lsrm cosθer + 23π

Assuming a sinusoidal distribution of windings, it may be easily shown that

Lsrm = Lms ⋅Lrmr (13.3) Reducing the rotor to stator is useful especially for cage rotor IMs, no access to rotor variables is available.

In this case, the mutual inductance becomes equal to self inductance L_srm Æ

L_sm and the rotor self inductance equal to the stator self inductance L_mr^r Æ L_sm.

To conserve the fluxes and losses with stator reduced variables,

iarr = iibrrbr = iicrcrr = LLsrmsm = Krs iar	(13.4)
Vararr = VVbrbrr = VVcrcrr = iiararr = iibrbrr = iicrcrr = K1rs V	(13.5)
Rrr = Lrlr = 1 2	(13.6)

Rr Llr Krs

The expressions of rotor resistance R_r, leakage inductance L_lr, both reduced to the stator for both cage and wound rotors are given in Chapter 6.

The same is true for R_s, L_ls of the stator. The magnetization self inductance L_sm has been calculated in Chapter 5.

Now the matrix form of phase coordinate (variable) model is

[ ] [ ][]V = R i + ^d [ ]Ψ

dt

[ ]V ⁼ [V ,V ,V ,V ,V ,V_{a b c a r br cr} ]^T (13.7)

[]i = [i ,i ,i ,ia b c a r ,ibr ,icr ]T

[ ]R = Diag R ,R ,R ,R ,R ,R[ _{s s s r r r} ]

[ ]Ψ = [Labca b cr r r (θer )][]i (13.8)

[Labcar r rb c (θer )]=



 Lls +Lsm −Lsm /2 −Lsm /2 Lsm cosθer



 −Lsm /2 Lls +Lsm −Lsm /2 Lsrm cosθ −er 23π



 −Lsm /2 −Lsm /2 Lls +Lsm Lsrm cosθ +er 2π

  3 

= Lsm cosθer Lsrm cosθ −er 23π Lsrm cosθ +er 23π Lls +Lsm L cosθ +er 2π Lsm cosθer Lsrm cosθ −er 2π −Lsm /2 srm

  3   3 

 θ − 2π Lsrm cos er 3  Lsrm cosθ +er 23π Lsm cosθer −Lsm /2

With (13.8), (13.7) becomes

L_srm cosθ +_er 2π L_srm cosθ −_er 2π_

 3   3 

Lsm cosθer Lsrm cosθ +er 23π

Lsrm cosθ −er 23π Lsm cosθer 

−Lsm /2 −Lsm /2 



Lls +Lsm −Lsm /2 



−Lsm /2 Lls +Lsm 



(13.9)

  _∂i _{ } dt d_θer ^ddt^θer (13.10)

Multiplying (13.10) by [i]^T we get

[] [ ] []i ^T V = i ^T R i[]+ dt^{d } ¹2[ ][][]L i i ^T ^+ ¹2 []i ^T d_θ^der [ ][]L i ω_r (13.11)

The first term represents the winding losses, the second, the stored magnetic energy variation, and the third, the electromagnetic power P_e.

P_e = T_e ωp^r = ¹2 []i ^{T d L}d^{[ ]}_θer []i ω_r (13.12)

1

The electromagnetic torque T_e is

Te = 12 p i1[]T d Ld[ ]θer []i (13.13)

The motion equation is

pJ ddtωr = Te −Tload; ddtθer = ωr (13.14)

1

An 8^th order nonlinear model with time-variable coefficients (inductances) has been obtained, even with core loss neglected.

Numerical methods are required to solve it, but the computation time is prohibitive. Consequently, the phase coordinate model is to be used only for special cases as the inductance and resistance matrix may be assigned any values and rotor position dependencies.

The complex or space variable model is now introduced to get rid of rotor position dependence of parameters.

THE COMPLEX VARIABLE MODEL

Let us use the following notations:

a = ej2³π; cos= Re a ; cos[ ]= Re a[ ]2

(13.15)

cosθer + 2π = Re ae[ jθer ]; cosθer + 4π = Re a e[ 2 jθer ];

 3   3 

Based on the inductance matrix, expression (13.9), the stator phase a and rotor phase a_r flux linkages Ψ_a and Ψ_ar are

Ψ =a L ils a + Lms Re i[ a +aib +a i2 c ]+ Lms Re i[( a r +aibr +a i2 cr )ejθer ] (13.16) Ψar = L ilr ar + Lms Re i[ ar +aibr +a i2 cr ]+ Lms Re i[( a +aib +a i e2 c ) − θj er ] (13.17)

We may now introduce the following complex variables as space phasors:

[1]

iss = 2 (ia +aib +a i2 c ) 3	(13.18)
irr = 2 (iar +aibr +a i2 cr ) 3 Also,	(13.19)
Re i ss  = ia − 13(ia +ib +ic )	(13.20)
Re i rr  = ia r − 13(ia r +ibr +icr ) In symmetric steady-state and transient regimes,	(13.21)
ia +ib +ic = iar +ibr +icr = 0 With the above definitions, Ψa and Ψar become	(13.22)
 s   s r jθ  3	(13.23)
Ψ =a L Re ils  s + L Re im  s +i er er ; Lm = 2 Lms
Ψar = L Re ilr  rr + L Re im  rr +i ess − θj er 	(13.24)

Similar expressions may be derived for phases b_r and c_r. After adding them together, using the complex variable definitions (13.18) and (13.19) for flux linkages and voltages, also, we obtain

s

Vs^s = R i^s s^s d^dtΨs ; Ψ =ss L is ss + L i em rr jθer ; (13.25) +

_r

where	Vrr = R ir rr + d r ; Ψ =rr L ir rr + L i em ss − θj er dt
	Ls = Lsl + L ;m Lr = Lrl + Lm	(13.26)

Ψ

Vss = 23 (Va +aVb +a V ; V2 c ) rr = 23 (Var +aVbr +a V2 cr ) (13.27) In the above equations, stator variables are still given in stator coordinates and rotor variables in rotor coordinates.

Making use of a rotation of complex variables by the general angle θ_b in the stator and θ_b – θ_er in the rotor, we obtain all variables in a unique reference rotating at electrical speed ω_b,

ω =b d b dt

(13.28)

^θ

Ψ = Ψs b jθ

Ψ = Ψr bs j(θ −θb s eer ); b ; irr i=ss =i erb i esbj(θ −θjbθb ; er );V ssV=rr V e=sbV ejbrθb ;j(θ −θb er ) (13.29)

r r e

With these new variables Equations (13.25) become

Vs = R is s + dΨs + ω Ψj

dt b s ; Ψ =s L is s + L im r (13.30)

Vr = R ir r + dΨr + j(ω −ω Ψb r ) r ; Ψ =r L ir r + L im s

dt

For convenience, the superscript b was dropped in (13.30). The electromagnetic torque is related to motion-induced voltage in (13.30).

T_{e 1} (13.31)

Adding the equations of motion, the complete complex variable (spacephasor) model of IM is obtained.

J dωr = Te −Tload; dθer = ωr (13.32)

p₁ dt dt

The complex variables may be decomposed in plane along two orthogonal d and q axes rotating at speed ω_b to obtain the d–q (Park) model. [2]

Vs = Vd + j V ; i⋅ qs = id + j i ; ⋅ q Ψ = Ψ +s d j⋅Ψq (13.33)

Vr = V_dr + j V ; i⋅ _qr r = i_dr + j i ; ⋅ _qr Ψ = Ψ +_{r dr} j⋅Ψ_qr

With (13.33), the voltage Equations (13.30) become

ddtΨd = Vd −Rs ⋅id +ω ⋅Ψb q ddtΨq = Vq −Rs ⋅iq −ω ⋅Ψb d

dΨdtdr = Vdr −Rr ⋅idr + ω −( b ω ⋅Ψr ) qr (13.34)

dΨdtqr = Vqr −Rr ⋅iqr − ω −( b ω ⋅Ψr ) dr

Te 1 d q q d 1 m q dr d qr

Also from (13.27) with (13.19), the Park transformation for stator P(θ_b) is

derived.

V_d  V_a 

_Vq _ = [P( )θb ]⋅_Vb _ (13.35)

V0  Vc 

^cos(−θ_b ) cos^−θ +_b ²3^π

[P( )θb ]= 23 ⋅sin(−θb ) sin−θ +b 23π 



 1 1

 2 2

The inverse Park transformation is

cos^−θ −_b ²3^π^ sin^−θ −_b ²3^{π }^_ (13.36)

1 

2 

^T (13.37)

A similar transformation is valid for the rotor but with θ_b – θ_er instead of θ_b.

It may be easily proved that the homopolar (real) variables V₀, i₀, V_0r, i_0r,

Ψ₀, Ψ_0r do not interface in energy conversion

d 0 s 0 0 L0s i0

dΨdt_0r = V_0r −R_r ⋅i ;_0r ^Ψ_0r ≈ L_0r ⋅i₀ (13.38)

L_0s and L_0r are the homopolar inductances of stator and rotor. Their values are equal or lower (for chorded coil windings) to the respective leakage inductances L_ls and L_lr.

A few remarks on the complex variable (space phasor) and d–q models are in order.

• Both models include, in the form presented here, only the space fundamental of mmfs and airgap flux distributions.

• Both models exhibit inductances independent of rotor position.

• The complex variable (space phasor) model is credited with a reduction in the number of equations with respect to the d–q model but it operates with complex variables.

• When solving the state space equations, only the d–q model, with real variables, benefits the existing commercial software (Mathematica, Matlab– Simulink, Spice, etc.).

• Both models are very practical in treating the transients and control of symmetrical IMs fed from symmetrical voltage power grids or from PWM converters.

• Easy incorporation of magnetic saturation and rotor skin effect are two additional assets of complex variable and d–q models. The airgap flux density retains a sinusoidal distribution along the circumferential direction.

• Besides the complex variable which enjoys widespread usage, other models (variable transformations), that deal especially with asymmetric supply or asymmetric machine cases have been introduced (for a summary see Reference. [3, 4])