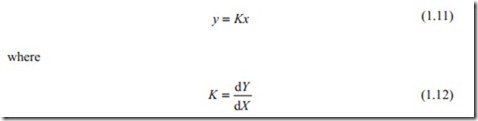Linearization Technique
If there is a continuous nonlinearity in the form of
Feedback Control Theory
In Eqs. (1.10) and (1.9) x, y represent small perturbation from the equilibrium point. Equation (1.10) can be written as
K is constant at an operating point. Throughout this book, the lower case variable represents small perturbation from equilibrium point. This is shown in Fig. 1.3.
Equation (1.8) represents one variable system. For a multivariable system, similar linearized equation can be obtained.
The solution of the governing equation simplifies if Laplace Transform is used.
Related posts:
Rewinding and Reconnecting
Fundamentals of Electricity:a Closer look at atoms
FUNDAMENTALS OF ELECTRIC SYSTEMS:LENZ’S LAW
AUDIO AND VIDEO SYSTEMS - AM/FM TUNERS
Safety:electrostatic Discharge
OPERATING CHARACTERISTICS OF INDUCTION MOTORS:SPEED CONTROL
OPERATING CHARACTERISTICS OF INDUCTION MOTORS:SINGLE-PHASE INDUCTION MOTORS
summary Of Inductance
INDUCTION MACHINES IN APPLICATIONS
Troubleshooting variable speed drives:Gate-commutated inverters (DC/AC converters)
VIBRATION ANALYSIS:MACHINERY EXAMPLE AND VIBRATION ANALYSIS
Plugging
Stator and Coil Winding
Objective tests on transformer