Error Correction and Concealment
All practical recording and transmission media are imperfect. Magnetic media, for example, suffer from noise and dropouts. In a digital recording of binary data, a bit is either correct or wrong, with no intermediate stage. Small amounts of noise are rejected, but inevitably, infrequent noise impulses cause some individual bits to be in error. Dropouts cause a larger number of bits in one place to be in error. An error of this kind is called a burst error. Whatever the medium and whatever the nature of the mechanism responsible, data are either recovered correctly or suffer some combination of bit errors and burst errors. In optical disks, random errors can be caused by imperfections in the moulding process, whereas burst errors are due to contamination or scratching of the disk surface.
The audibility of a bit error depends on which bit of the sample is involved. If the LSB of one sample was in error in a detailed musical passage, the effect would be totally masked and no one could detect it. Conversely, if the MSB of one sample was in error during a pure tone, no one could fail to notice the resulting click. Clearly a means is needed to render errors from the medium inaudible. This is the purpose of error correction.
In binary, a bit has only two states. If it is wrong, it is only necessary to reverse the state and it must be right. Thus the correction process is trivial and perfect. The main difficulty is in identifying the bits that are in error. This is done by coding data by adding redundant bits. Adding redundancy is not confined to digital technology, airliners have several engines and cars have twin braking systems. Clearly the more failures that have to be handled, the more redundancy is needed.
In digital recording, the amount of error that can be corrected is proportional to the amount of redundancy. Consequently, corrected samples are undetectable. If the amount of error exceeds the amount of redundancy, correction is not possible, and, in order to allow graceful degradation, concealment will be used. Concealment is a process where the value of a missing sample is estimated from those nearby. The estimated sample value is not necessarily exactly the same as the original, and so under some circumstances concealment can be audible, especially if it is frequent. However, in a well-designed system, concealments occur with negligible frequency unless there is an actual fault or problem.
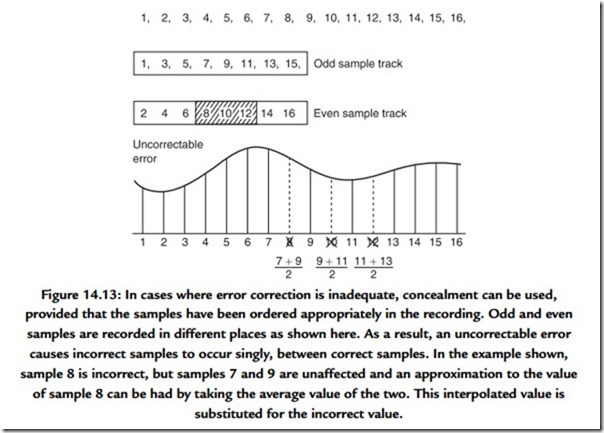
Concealment is made possible by rearranging the sample sequence prior to recording. This is shown in Figure 14.13 where odd-numbered samples are separated from even- numbered samples prior to recording. The odd and even sets of samples may be recorded in different places on the medium so that an uncorrectable burst error affects only one set. On replay, the samples are recombined into their natural sequence, and the error is now split up so that it results in every other sample being lost in two different places. In those places, the waveform is described half as often, but can still be reproduced with some loss of accuracy. This is better than not being reproduced at all even if it is not perfect. Most tape-based digital audio recorders use such an odd/even distribution for concealment. Clearly, if any errors are fully correctable, the distribution is a waste of time; it is only needed if correction is not possible.
The presence of an error-correction system means that the audio quality is independent of the medium/head quality within limits. There is no point in trying to assess the health of a machine by listening to the audio, as this will not reveal whether the error rate is normal or within a whisker of failure. The only useful procedure is to monitor the frequency with which errors are being corrected and to compare it with normal figures.
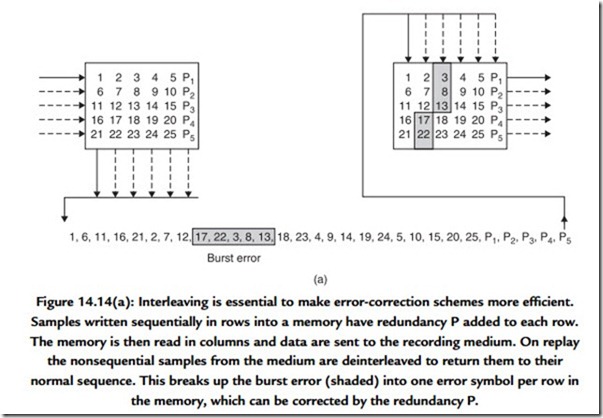
Digital systems such as broadcast channels, optical disks, and magnetic recorders are prone to burst errors. Adding redundancy equal to the size of expected bursts to every code is inefficient. Figure 14.14(a) shows that the efficiency of the system can be raised using interleaving. Sequential samples from the ADC are assembled into codes, but these are not recorded/transmitted in their natural sequence. A number of sequential codes are assembled along rows in a memory. When the memory is full, it is copied to the medium by reading down columns.
Subsequently, the samples need to be deinterleaved to return them to their natural sequence. This is done by writing samples from tape into a memory in columns, and when it is full, the memory is read in rows. Samples read from the memory are now in their original sequence so there is no effect on the information. However, if a burst error occurs, as is shown shaded on the diagram, it will damage sequential samples in a vertical direction in the deinterleave memory. When the memory is read, a single large error is broken down into a number of small errors whose sizes are exactly equal to the correcting power of the codes and the correction is performed with maximum efficiency.
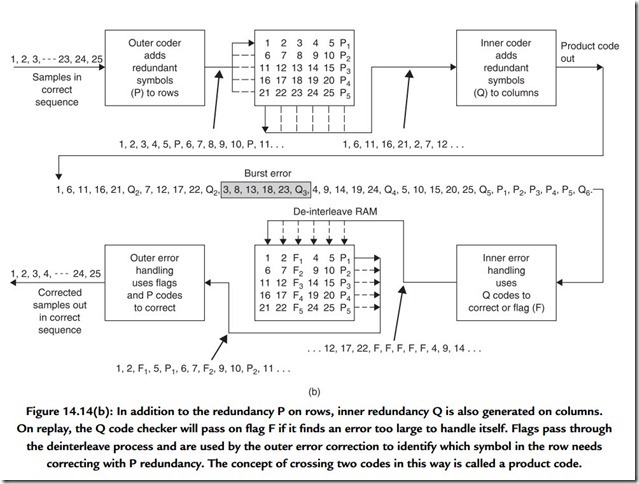
An extension of the process of interleave is where the memory array has not only rows made into code words but also columns made into code words by the addition of vertical redundancy. This is known as a product code. Figure 14.14(b) shows that in a product code the redundancy calculated first and checked last is called the outer code, and the redundancy calculated second and checked first is called the inner code. The inner code
is formed along tracks on the medium. Random errors due to noise are corrected by the inner code and do not impair the burst-correcting power of the outer code. Burst errors are declared uncorrectable by the inner code, which flags the bad samples on the way into the deinterleave memory. The outer code reads the error flags in order to locate erroneous data. As it does not have to compute the error locations, the outer code can correct more errors.
The interleave, deinterleave, time-compression, and time base-correction processes inevitably cause delay.