D.c. Motor:Motor Principle

Motor Principle

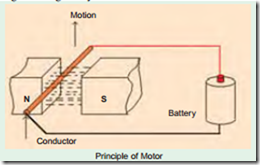
An Electric motor is a machine which converts electric energy into mechanical energy. Its action is based on the principle that when a current-carrying conductor is placed in a magnetic field, it experiences a mechanical force whose direction is given by Fleming’s Left-hand Rule and whose magnitude is given by F = BIl Newton.

Constructionally, there is no basic difference between a d.c. generator and a d.c. motor. In fact, the same d.c. ma- chine can be used interchangeably as a generator or as a motor. D.C. motors are also like generators, shunt-wound or series-wound or compound-wound.

In Fig. 29.1 a part of multipolar d.c. motor is shown. When its field magnets are excited and its armature conductors Conductor are supplied with current from the supply mains, they experience a force tending to rotate the armature. Armature conductors under N-pole are assumed to carry current downwards (crosses) and those under S-poles, to carry current upwards (dots). By applying Fleming’s Left-hand Rule, the direction of the force on

each conductor can be found. It is shown by small arrows placed above each conductor. It will be seen that each conductor can be found. It will be seen that each conductor experiences a force F which tends to rotate the armature in anticlockwise direction. These forces collectively produce a driving torque which sets the armature rotating.

It should be noted that the function of a commutator in the motor is the same as in a generator. By reversing current in each conductor as it passes from one pole to another, it helps to develop a continuous and unidirectional torque.

Comparison of Generator and Motor Action

As said above, the same d.c. machine can be used, at least theoretically, interchangeably as a N N generator or as a motor. When operating as a generator, it is driven by a mechanical machine and it develops voltage which in turn produces a current flow in an electric circuit. When operating as a motor, it is supplied by electric

current and it develops torque which in turn produces mechanical rotation.

Let us first consider its operation as a generator and see how exactly and through which agency, mechanical power is converted into electric power.

In Fig. 29.2 part of a generator whose armature is being driven clockwise by its prime mover is shown.

Fig. 29.2 (a) represents the fields set up independently by the main poles and the armature conductors like A in the figure. The resultant field or magnetic lines on flux are shown in Fig. 29.2 (b).

It is seen that there is a crowding of lines of flux on the right-hand side of A. These magnetic lines of flux may be likened to the rubber bands under tension. Hence, the bent lines of flux up a mechanical force on A much in the same way as the bent elastic rubber band of a catapult produces a mechanical force on the stone piece. It will be seen that this force is in a direction opposite to that of armature rotation. Hence, it is known as backward force or magnetic drag on the conductors. It is against this drag action on all armature conductor that the prime mover has to work. The work done in overcoming this opposition is converted into electric energy. Therefore, it should be clearly understood that it is only through the instrumentality of this magnetic drag that energy conversion is possible in a d.c. generator*.

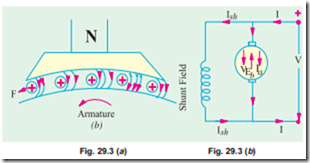
Next, suppose that the above d.c. machine is un- coupled from its prime mover and that current is sent through the armature conductors under a N-pole in the downward direction as shown in Fig. 29.3 (a). The conductors will again experience a force in the anticlockwise direction (Fleming’s Left hand Rule).

Hence, the machine will start rotating anticlockwise, thereby developing a torque which can produce mechanical rotation.

The machine is then said to be motoring.

As said above, energy conversion is not possible unless there is some opposition whose over- coming provides the necessary means for such conversion. In the case of a generator, it was the magnetic drag which provided the necessary opposition. But what is the equivalent of that drag in the case of a motor ? Well, it is the back e.m.f. It is explained in this manner :

As soon as the armature starts rotating, dynamically (or motionally) induced e.m.f. is produced in the armature conductors. The direction of this induced e.m.f. as found by Fleming’s Right-hand Rule, is outwards i.e., in direct opposition to the applied voltage (Fig. 29.3 (b)). This is why it is known as back e.m.f. Eb or counter e.m.f. Its value is the same as for the motionally induced e.m.f. in

the generator i.e. Eb = (FZN) ´ (P/A) volts. The applied voltage V has to be force current through the

armature conductors against this back e.m.f. Eb. The electric work done in overcoming this opposition is converted into mechanical energy developed in the armature. There- fore, it is obvious that but for the pro- + + duction of this opposing e.m.f. en- + + ergy conversion would not have been possible.

Now, before leaving this topic, let it be pointed out that in an actual motor with slotted armature, the torque is not due to mechanical force on the conductors themselves, but due to tangential pull on the armature teeth as shown in Fig. 29.4.

It is seen from Fig. 29.4 (a) that the main flux is concentrated in the form of tufts at the armature teeth while the armature flux is shown by the dotted lines embracing the armature slots. The effect of armature flux on the main flux, as shown in Fig. 29.4 (b), is two-fold :

(i) It increases the flux on the left-hand side of the teeth and decreases it on the right-hand side, thus making the distribution of flux density across the tooth section unequal.

(ii) It inclines the direction of lines of force in the air-gap so that they are not radial but are disposed in a manner shown in Fig. 29.4 (b). The pull exerted by the poles on the teeth can now be resolved into two components. One is the tangential component F1 and the other vertical component F2. The vertical component F2, when considered for all the teeth round the armature, adds up to zero. But the component F1 is not cancelled and it is this tangential component which, acting on all the teeth, gives rise to the armature torque.

Significance of the Back e.m.f.

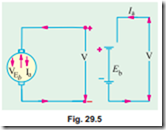
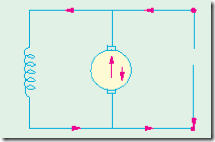
As explained in Art 29.2, when the motor armature ro- tates, the conductors also rotate and hence cut the flux. In ac- cordance with the laws of electromagnetic induction, e.m.f. is induced in them whose direction, as found by Fleming’s Right- hand Rule, is in opposition to the applied voltage (Fig. 29.5). Because of its opposing direction, it is referred to as counter e.m.f. or back e.m.f. Eb. The equivalent circuit of a motor is shown in Fig. 29.6. The rotating armature generating the back e.m.f. Eb is like a battery of e.m.f. Eb put across a supply mains of V volts. Obviously, V has to drive Ia against the opposition of Eb. The power required to overcome this opposition is EbIa.

In the case of a cell, this power over an interval of time is converted into chemical energy, but in the present case, it is converted into mechanical energy.

where Ra is the resistance of the armature circuit. As pointed out above, Eb = FZN ´ (P/A) volt where N is in r.p.s.

Back e.m.f. depends, among other factors, upon the armature speed. If speed is high, Eb is large, hence armature current Ia, seen from the above equation, is small. If the speed is less, then Eb is less, hence more current flows which develops motor torque (Art 29.7). So, we find that Eb acts like a governor i.e., it makes a motor self-regulating so that it draws as much current as is just necessary.

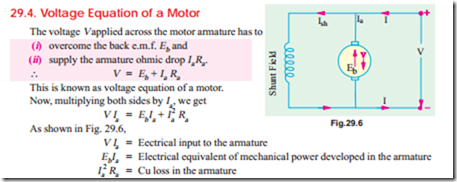
Voltage Equation of a Motor

Hence, out of the armature input, some is wasted in I2R loss and the rest is converted into mechanical power within the armature.

It may also be noted that motor efficiency is given by the ratio of power developed by the armature to its input i.e., EbIa/V Ia = Eb/V. Obviously, higher the value of Eb as compared to V, higher the motor efficiency.

Condition for Maximum Power

The gross mechanical power developed by a motor is Pm = V Ia – Ia Ra.

Differentiating both sides with respect to Ia and equating the result to zero, we get

Thus gross mechanical power developed by a motor is maximum when back e.m.f. is equal to half the applied voltage. This condition is, however, not realized in practice, because in that case current would be much beyond the normal current of the motor. Moreover, half the input would be wasted in the form of heat and taking other losses (mechanical and magnetic) into consideration, the motor efficiency will be well below 50 percent.

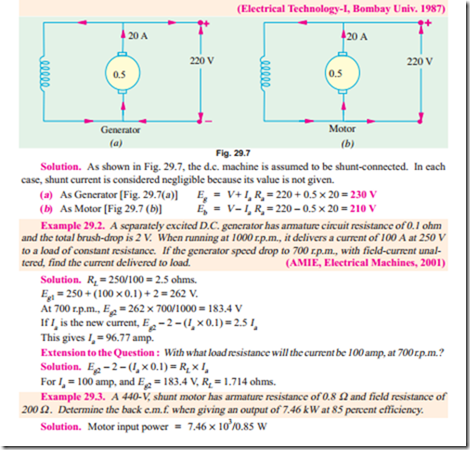
Example 29.1. A 220-V d.c. machine has an armature resistance of 0.5 W. If the full-load armature current is 20 A, find the induced e.m.f. when the machine acts as (i) generator (ii) motor.

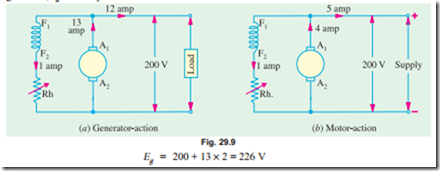
Example 29.5. A 4 pole, 32 conductor, lap-wound d.c. shunt generator with terminal voltage of 200 volts delivering 12 amps to the load has ra = 2 and field circuit resistance of 200 ohms. It is driven at 1000 r.p.m. Calculate the flux per pole in the machine. If the machine has to be run as a motor with the same terminal voltage and drawing 5 amps from the mains, maintaining the same magnetic field, find the speed of the machine. [Sambalpur University, 1998]

Solution. Current distributions during two actions are indicated in Fig. 29.9 (a) and (b). As a generator, Ia = 13 amp

Tutorial Problems 29.1

1. What do you understand by the term ‘back e.m.f.’ ? A d.c. motor connected to a 460-V supply has an armature resistance of 0.15 W. Calculate

(a) The value of back e.m.f. when the armature current is 120 A.

(b) The value of armature current when the back e.m.f. is 447.4 V. [(a) 442 V (b) 84 A]

2. A d.c. motor connected to a 460-V supply takes an armature current of 120 A on full load. If the armature circuit has a resistance of 0.25 W, calculate the value of the back e.m.f. at this load. [430 V]

3. A 4-pole d.c. motor takes an armature current of 150 A at 440 V. If its armature circuit has a resistance of 0.15 W, what will be the value of back e.m.f. at this load ? [417.5 V]

Torque

By the term torque is meant the turning or twisting moment of a force about an axis. It is measured by the product of the force and the radius at which this force acts.