The Replay System
Physical Characteristics
For the reasons shown earlier, the minimum bandwidth required to store the original 20-Hz to 20-kHz stereo signal in digitally encoded form has now been increased 215-fold, to some 4.3 MHz. It is, therefore, no longer feasible to use a record/replay system based on an undulating groove formed on the surface of a vinyl disc because the excursions in the groove would be impracticably close together unless the rotational speed of the disc were to be enormously increased, which would lead to other problems, such as audible replay noise, pick-up tracking difficulties, and rapid surface wear.
The technique adopted by Philips/Sony in the design of the CD replay system is therefore based on an optical pick-up mechanism, in which the binary coded ‘0’s and ‘1’s are read from a spiral sequence of bumps on an internal reflecting layer within a rapidly rotating (approximately 400 rpm) transparent plastic disc. Because the replay system is noncontacting, this also offers the advantage that there is no specific disc wear incurred in the replay of the records and they have, in principle, if handled carefully, an indefinitely long service life.
Additional Data Encoded on Disc
● Error correction data.
● Control data—total and elapsed playing times, number of tracks, end of playing area, preemphasis [may be added using either 15 μs (10,610 Hz) or 50 μs
(3183 Hz) time constants], and so on.
● Synchronization signals added to define beginning and end of each data block.
● Merging bits used with EFM.
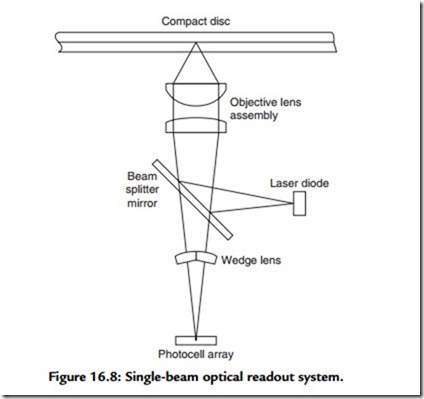
Optical Readout System
This is shown, schematically, in Figure 16.8, and consists of an infra-red laser light source (GaAIAs, 0.5 mW, 780 nm), which is focused on a reflecting layer buffed about 1 mm beneath the transparent “active” surface of the disc being played. This metallic
reflecting layer is deformed in the recording process to produce a sequence of oblong humps along the spiral path of the recorded track (actually formed by making pits on the reverse side of the disc prior to metallization). Because of the shallow depth of focus of the lens, due to its large effective numerical aperture (f/0.5) and the characteristics of the laser light focused on the reflecting surface, these deformations of the surface greatly diminish the intensity of the incident light reflected to the receiver photocell, in comparison with that from the fiat mirror-like surface of the undeformed disc. This causes the intensity of the light reaching the photocell to fluctuate as the disc rotates and causes the generation of the high-speed sequence of electrical ‘0’s and ‘1’s required to reproduce the digitally encoded signal.
The signals representing ‘1’s are generated by a photocell output level transition, either up or down, while ‘0’s are generated electronically within the system by the presence of a timing impulse that is not coincident with a received ‘1’ signal. This confers the valuable feature that the system defaults to a ‘0’ if a data transition is not read, and such random errors can be corrected with ease in the replay system.
It is necessary to control the position of the lens, in relation both to the disc surface and to the recorded spiral sequence of surface lumps, to a high degree of accuracy. This is done by high-speed closed-loop servo-mechanism systems, in which the vertical and lateral position of the whole optical readout assembly is precisely adjusted by electro- mechanical actuators, which are caused to operate in a manner that is very similar to the voice coil in a moving coil loudspeaker.
Two alternative arrangements are used for positioning the optical readout assembly, of which the older layout employs a sled-type arrangement that moves the whole unit in a rectilinear manner across the active face of the disc. This maintains the correct angular position of the head, in relation to the recorded track, necessary when a “three-beam” track position detector is used. Recent CD replay systems more commonly employ a single-beam lateral/vertical error detection system. Since this is insensitive to the angular relationship between the track and the head, it allows a simple pivoted arm structure to be substituted for the rectilinear-motion sled arrangement. This pivoted arm layout is less expensive to produce, is less sensitive to mechanical shocks, and allows more rapid scanning of the disc surface when searching for tracks.
Some degree of immunity from readout errors due to scratches and dust on the active surface of the disc is provided by the optical characteristics of the lens, which has a sufficiently large aperture and short focal length that the surface of the disc is out of focus when the lens is accurately focused on the plane of the buried mirror layer.
Electronic Characteristics
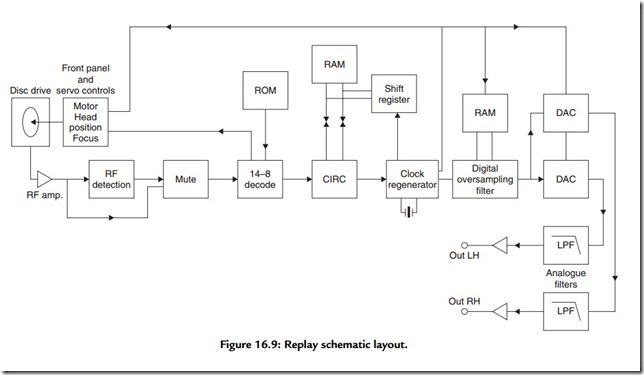
The electronic replay system follows a path closely similar to that used in the encoding of the original recorded signal, although in reverse order, and is shown schematically in Figure 16.9. The major differences between record and replay paths are those such as “oversampling,” “digital filtering,” and “noise shaping” intended to improve the accuracy of, and reduce the noise level inherent in, the digital-to-analogue transformation.
Referring to Figure 16.9, the RF electrical output of the disc replay photocell, after amplification, is fed to a simple signal detection system, which mutes the signal chain in the absence of a received signal, to ensure intertrack silence. If a signal is present, it is then fed to the EFM decoder stage where the interface and “joining” bits are removed, and the signal is passed as a group of 8-bit symbols to the CIRC error correction circuit, which permits a very high level of signal restoration.
An accurate crystal-controlled clock regeneration circuit then causes the signal data blocks to be withdrawn in correct order from a sequential memory “shift register” circuit and reassembled into precisely timed and numerically accurate replicas of the original pairs of 16-bit (left and fight channel) digitally encoded signals. The timing information from this stage is also used to control the speed of the disc drive motor and ensure that signal data are recovered at the correct bit rate.
The remainder of the replay process consists of the stages in which the signal is converted back into analogue form, filtered to remove the unwanted high-frequency components, and reconstructed, as far as possible, as a quantization noise-free copy of the original input waveform. As noted earlier, the filtering and the accuracy of reconstruction of this waveform are helped greatly by the process of “oversampling” in which the original sampling rate is increased, on replay, from 44.1 kHz to some multiple of this frequency, such as 176.4 kHz or even higher. This process can be done by a circuit in which the numerical values assigned to the signal at these additional sampling points are obtained by interpolation between the original input digital levels. As a matter of convenience, the same circuit arrangement will also provide a steep-cut filter having a near-zero transmission at half the sampling frequency.
The “Eight to Fourteen Modulation” Technique
This is a convenient shorthand term for what should really be described as “8-bit to 14-bit encoding/decoding” and is done for considerations of mechanical convenience in the record/replay process. As noted earlier, the ‘1’s in the digital signal flow are generated by transitions from low to high, or from high to low, in the undulations on the reflecting surface of the disc. On a statistical basis, it would clearly be possible, in an 8-bit encoded signal, for a string of eight or more ‘1’s to occur in the bit sequence, the recording of which would require a rapid sequence of surface humps with narrow gaps between them, making this inconvenient to manufacture. Also, in the nature of things, because these pits or humps will never have absolutely square, clean-cut edges, transitions from one sloping edge to another, where there is such a sequence of closely spaced humps, would also lead to a reduction in the replay signal amplitude and might cause lost data bits.
However, a long sequence of ‘0’s would leave the mirror surface of the disc unmarked by any signal modulation at all, and, bearing in mind the precise track and focus tolerances demanded by the replay system, this absence of signals at the receiver photocell would embarrass the control systems that seek to regulate the lateral and vertical position of the spot focused on the disc and that use errors found in the bit repetition frequency, derived from the recovered sequence of ‘1’s and ‘0’s, to correct inaccuracies in the disc rotation speed. All these problems would be worsened in the presence of mechanical vibration.
The method chosen to solve this problem is to translate the 256-bit sequences possible with an 8-bit encoded signal into an alternative series of 256-bit sequences found in a 14-bit code, which are then reassembled into a sequence of symbols as shown graphically in Figure 16.7. The requirements for the alternative code are that a minimum of two ‘0’s shall separate each ‘1’ and that no more than ten ‘0’s shall occur in sequence. In the 14-bit code, there are 267 values that satisfy this criterion, of which 256 have been chosen and stored in a ROM-based “look-up” table. As a result of the EFM process, there are only nine different pit lengths that are cut into the disc surface during recording, varying from 3 to 11 clock periods in length.
Because the numerical magnitude of the output (EFM) digital sequence is no longer directly related to that of the incoming 8-bit word, the term “symbol” is used to describe this or other similar groups of bits.
Since the EFM encoding process cannot by itself ensure that the junction between consecutive symbols does not violate the requirements noted earlier, an “interface” or “coupling” group of three bits is also added, at this stage, from the EFM ROM store, at the junction between each of these symbols. This coupling group will take the form of a ‘000’, ‘100’, ‘010’, or ‘001’ sequence, depending on the position of the ‘0’s or ‘1’s at the end of the EFM symbol. As shown in Figure 16.6, this process increases the bit rate from 1.882 to 4.123 MB/s, and the further addition of uniquely styled 24-bit synchronizing words to hold the system in coherence, and to mark the beginnings of each bit sequence, increases the final signal rate at the output of the recording chain to 4.322 MB/s. These additional joining and synchronizing bits are stripped from the signal when the bit stream is decoded during the replay process.
Digital-to-Analogue Conversion
The transformation of the input analogue signal into, and back from, a digitally encoded bit sequence presents a number of problems. These stem from the limited time (22.7 μs) available for the conversion of each signal sample into its digitally encoded equivalent and from the very high precision needed in allocating numerical values to each sample. For example, in a 16-bit encoded system the magnitude of the MSB will be 32,768 times as large as the LSB. Therefore, to preserve the significance of a ‘0’ to ‘1’ transition in the LSB, both the initial and the long-term precision of the electronic components used to define the size of the MSB would need to be better than ±0.00305%. (A similar need for accuracy obviously also exists in the ADC used in recording.)
Bearing in mind that even a 0.1% tolerance component is an expensive item, such an accuracy requirement would clearly present enormous manufacturing difficulties. In addition, any errors in the sizes of the steps between the LSB and the MSB would lead to waveform distortion during the encoding/decoding process: a distortion that would worsen as the signal became smaller.
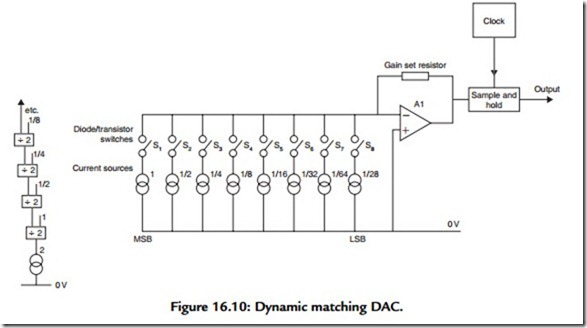
Individual manufacturers have their own preferences in the choice of digital-to-analogue conversion (DAC) designs, but a Philips system is illustrated, schematically, by way of example, in Figure 16.10, is an arrangement called “dynamic element matching.” In this circuit, outputs from a group of current sources, in a binary size sequence from 1 to 1/128, are summed by the amplifier A1, whose output is taken to a simple “sample
and hold” arrangement to recover the analogue envelope shape from the impulse stream generated by the operation of the A1 input switches (S1–S8). The required precision of the ratios between the input current sources is achieved by the use of switched resistor– capacitor current dividers, each of which is only required to divide its input current into two equal streams.
Since the input “16-bit” encoded signal is divided into two “8-bit” words in the CD replay process, representing the MS and LS sections from e1 to e8 and from e9 to e16, these two 8-bit digital words can be separately D/A converted, with the outputs added in an appropriate ratio to give the final 16-bit D/A conversion.
Digital Filtering and “Oversampling”
It was noted previously that Philips’ original choice of sampling frequency (44.1 kHz) and of signal bandwidth (20 Hz to 20 kHz) for the CD imposed the need for steep-cut filtering both prior to the ADC and following the DAC stages. This can lead to problems caused by propagation delays and phase shifts in the filter circuitry, which can degrade the sound quality. Various techniques are available that can lessen these problems, of which the most commonly used come under the headings of “digital filtering” and “oversampling.” Because these techniques are interrelated, I have lumped together the descriptions of both of these.
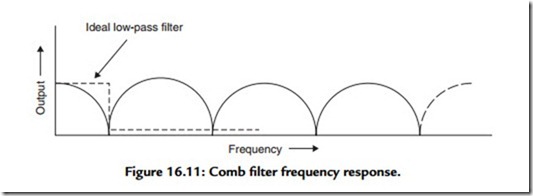
There are two practicable methods of filtering used with digitally encoded signals. For these signals, use can be made of the effect that if a signal is delayed by a time interval, Ts, and this delayed signal is then combined with the original input, signal cancellation— partial or complete—will occur at those frequencies where Ts is equal to the duration of an odd number of half cycles of the signal. This gives what is known as a “comb filter” response, shown in Figure 16.11, and this characteristic can be progressively augmented to approach an ideal low-pass filter response (100% transmission up to some chosen frequency, followed by zero transmission above this frequency) by the use of a number of further signal delay and addition paths having other, carefully chosen, gain coefficients and delay times. (Although, in principle, this technique could also be used on a signal in analogue form, there would be problems in providing a nondistorting time delay mechanism for such a signal—a problem that does not arise in the digital domain.)
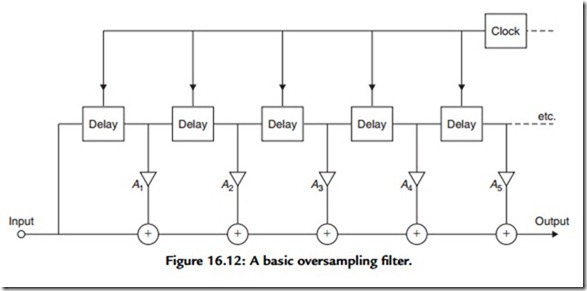
However, this comb filter type arrangement is not very conveniently suited to a system, such as the replay path for a CD, in which all operations are synchronized at a single specific “clock” frequency or its submultiples, and an alternative digital filter layout, shown in Figure 16.12 in simplified schematic form, is normally adopted instead. This provides a very steep-cut low-pass filter characteristic by operations carried out on the signal in its binary-encoded digital form.
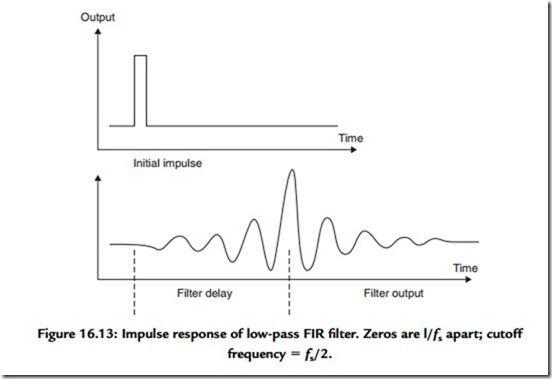
In this circuit, the delay blocks are “shift registers,” through which the signal passes in a “first in, first out” sequence at a rate determined by the clock frequency. Filtering is achieved in this system by reconstructing the impulse response of the desired low-pass filter circuit, such as that shown in Figure 16.13. The philosophical argument is that if a circuit can be made to have the same impulse response as the desired low-pass filter, it will also have the same gain/frequency characteristics as that filter—a postulate that experiment shows to be true.
This required impulse response is built up by progressive additions to the signal as it passes along the input-to-output path, at each stage of which the successive delayed binary coded contributions are modified by a sequence of mathematical operations. These are carded out, according to appropriate algorithms, stored in “look-up” tables, by the coefficient multipliers A1, A2, A3 , . . . , An. (The purpose of these mathematical manipulations is, in effect, to ensure that those components of the signal that recur more
frequently than would be permitted by the notional “cut-off ” frequency of the filter will all have a coded equivalent to zero magnitude.) Each additional stage has the same attenuation rate as a single-pole RC filter (–6 dB/octave), but with a strictly linear phase characteristic, which leads to zero group delay.
This type of filter is known either as a “transversal filter,” from the way in which the signal passes through it, or a “finite impulse response” (FIR) filter because of the deliberate omission from its synthesized impulse response characteristics of later contributions from the coefficient multipliers. (There is no point in adding further terms to the A1, . . . , An series when the values of these operators tend to zero.)
Some contemporary filters of this kind use 128 sequential “taps” to the transmission chain, giving the equivalent of a –768-dB/octave low-pass filter. This demonstrates, incidentally, the advantage of handling signals in the digital domain in that a 128-stage analogue filter would be very complex and also have an unacceptably high thermal noise background.
If the FIR clock frequency is increased to 176.4 kHz, the action of the shift registers will be to generate three further signal samples and to interpolate these additional samples between those given by the original 44.1-kHz sampling intervals—a process termed “four times oversampling.”
The simple sample-and-hold stage, at the output of the DAC shown in Figure 16.10, will also assist filtering, as it will attenuate any signals occurring at the clock frequency to an extent determined by the duration of the sampling operation—called the sampling “window.” If the window length is near 100% of the cycle time, attenuation of the S/H circuit will be nearly total at fs.
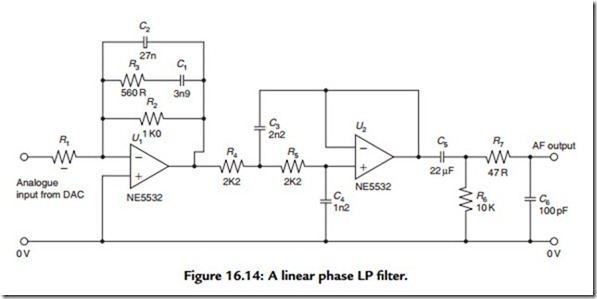
Oversampling, on its own, would have the advantage of pushing the aliasing frequency up to a higher value, which makes the design of the antialiasing and waveform reconstruction filter a much easier task to accomplish using simple analogue-mode low-pass filters whose characteristics can be tailored so that they introduce very little unwanted group delay and phase shift. A typical example of this approach is the linear phase analogue filter design, shown in Figure 16.14, used following the final 16-bit DACs in the replay chain.
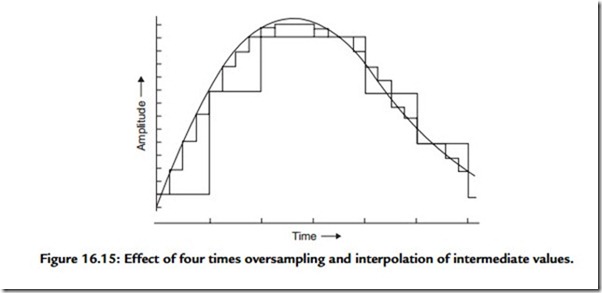
However, the FIR filter shown in Figure 16.12 has the additional effect of computing intermediate numerical values for the samples interpolated between the original 44.1-kHz input data, which makes the discontinuities in the PCM step waveform
smaller, as shown in Figure 16.15. This reduces the quantization noise and also increases the effective resolution of the DAC. As a general rule, an increase in the replay sampling rate gives an improvement in resolution equivalent to that given by a similar increase in encoding level, such that a four times oversampled 14-bit decoder would have the same resolution as a straight 16-bit decoder.
Yet another advantage of oversampling is that it increases the bandwidth over which the “quantization noise” will be spread—from 22.05 to 88.2 kHz in the case of a four times oversampling system. This reduces the proportion of the total noise that is now present within the audible (20 Hz to 20 kHz) part of the frequency spectrum—especially if “noise shaping” is also employed. This aspect is examined later in this chapter.
“Dither”
If a high-frequency noise signal is added to the waveform at the input to the ADC and if the peak-to-peak amplitude of this noise signal is equal to the quantization step ‘Q’,
both the resolution and the dynamic range of the converter will be increased. The reason for this can be seen if we consider what would happen if the actual analogue signal level were to lie somewhere between two quantization levels. Suppose, for example, in the case of an ADC, that the input signal had a level of 12.4 and that the nearest quantization levels were 12 and 13. If dither had been added, and a sufficient number of samples were taken, one after another, there would be a statistical probability that 60% of these
would be attributed to level 12 and that 40% would be attributed to level 13 so that, on averaging, the final analogue output from the ADC/DAC process would have the correct value of 12.4.
A further benefit is obtained by the addition of dither at the output of the replay DACs (most simply contrived by allowing the requisite amount of noise in the following analogue low-pass filters) in that it will tend to mask the quantization “granularity” of the recovered signal at low bit levels. This defect is particularly noticeable when the signal frequency happens to have a harmonic relationship with the sampling frequency.
The “Bitstream” Process and “Noise Shaping”
A problem in any analogue-to-digital or digital-to-analogue converter is that of obtaining an adequate degree of precision in the magnitudes of the digitally encoded steps. It has been seen that the accuracy required, in the most significant bit in a 16-bit converter, was better than 0.00305% if ‘0’–’1’ transitions in the LSB were to be significant. Similar, although lower, orders of accuracy are required from all the intermediate step values. Achieving this order of accuracy in a mass-produced consumer article is difficult and expensive. In fact, differences in tonal quality between CD players are likely to be due, in part, to inadequate precision in the DACs.
As a means of avoiding the need for high precision in the DAC converters, Philips took advantage of the fact that an effective improvement in resolution could be achieved merely by increasing the sampling rate, which could then be traded-off against the number of bits in the quantization level. Furthermore, whatever binary encoding system is adopted, the first bit in the received 16-bit word must always be either a ‘0’ or a ‘1’, and in the “two’s complement” code used in the CD system, the transition in the MSB from ‘0’ to ‘1’ and back will occur at the midpoint of the input analogue signal waveform.
This means that if the remaining 15 bits of a 16-bit input word are stripped off and discarded, this action will have the effect that the input digital signal will have been converted—admittedly somewhat crudely—into a voltage waveform of analogue form. Now, if this ‘0/1’ signal is 256 times oversampled, in the presence of dither, an
effective 9-bit resolution will be obtained from two clearly defined and easily stabilized quantization levels: a process for which Philips coined the term “bit stream” decoding.
Unfortunately, such a low-resolution quantization process will incur severe quantization errors that manifest as a high background noise level. Philips’ solution to this is to
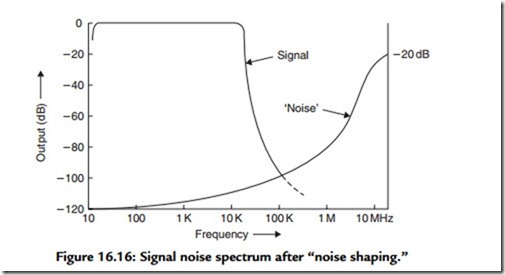
employ “noise shaping,” a procedure in which, as shown in Figure 16.16, the noise components are largely shifted out of the 20-Hz to 20-kHz audible region into the inaudible upper reaches of the new 11.29-MHz bandwidth.
The proposition is, in effect, that a decoded digital signal consists of the pure signal, plus a noise component (caused by the quantization error) related to the lack of resolution of the decoding process. It is further argued that if this noise component is removed by filtering, what remains will be the pure signal—no matter how poor the actual resolution of the decoder. Although this seems an unlikely hypothesis, users of CD players employing the “bit stream” system seem to agree that the technique does indeed work in practice. It would therefore seem that the greater freedom from distortion, which could be caused by errors in the quantization levels in high bit-level DACs, compensates for the crudity of a decoding system based on so few quantization steps.
Mornington-West1 quotes oversampling values of 758 and 1024 times, respectively, for “Technics” and “Sony” “low-bit” CD players, which would be equivalent in resolution to 10.5- and 11-bit quantization if a simple ‘0’ or ‘1’ choice of encoding levels was used. Since the presence of dither adds an effective 1 bit to the resolution and dynamic range, the final figures would become 10-, 11.5-, and 12-bit resolution, respectively, for the Philips, Technics, and Sony CD players.
However, such decoders need not use the single-bit resolution adopted by Philips, and if a 2- or 4-bit quantization was chosen as the base to which the oversampling process was applied—an option that would not incur significant problems with accuracy of quantization—this would provide low-bit resolution values as good as the 16-bit equivalents at a lower manufacturing cost and with greater reproducibility. Ultimately, the limit to the resolution possible with a multiple sampling decoder is set by the time “jitter” in the switching cycles and the practicable operating speeds of the digital logic elements used in the shift registers and adders. In the case of the 1024 times oversampling “Sony” system, a 44.1584-MHz clock speed is required, which is near the currently available limit.