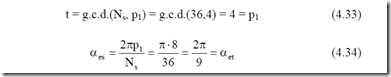Fractional q a.c. windings are not typical for induction motors due to their inherent pole asymmetry as slot/phase allocation under adjacent poles is not the same in contrast to integer q three-phase windings. However, with a small q (q ≤ 3) to reduce the harmonics content of airgap flux density, by increasing the order of the first slot harmonic from 6q ± 1 for integer q to 6(ac + b) ± 1 for q = (ca + b)/c = fractional two-layer such windings are favoured to single-layer versions. To set the rules to design such a standard winding–with identical coils–we proceed with an example.
Let us consider a small induction motor with 2p1 = 8 and q = 3/2, m = 3. The total number of slots Ns = 2p1qm = 2⋅4⋅3/2⋅3 = 36 slots. The coil span y is
y = integer(Ns/2p1) = integer(36/8) = 4slot pitches (4.31)
The parameters t,
The count of distinct arrows in the star of slot emf phasors is Ns/t = 36/4 = 9. This shows that the slot/phase allocation repeats itself after each pole pair (for an integer q it repeats after each pole). Thus mmf subharmonics, or fractional space harmonics, are still absent in this case of fractional q. This property holds for any q = (2l + 1)/2 for two-layer configurations.
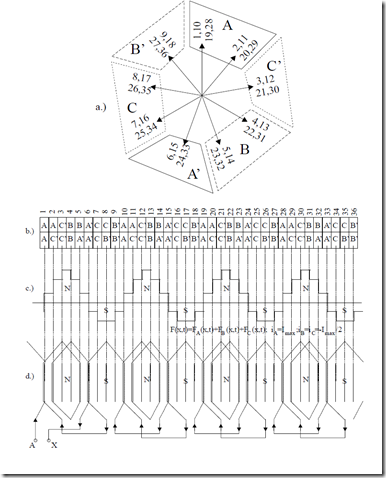
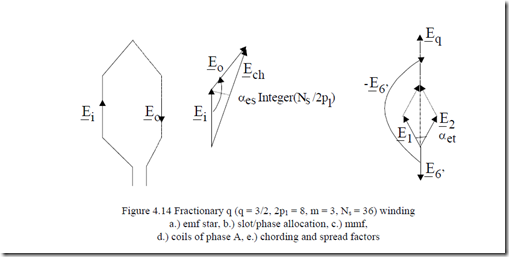
The star of slot emf phasors has q arrows and the counting of them is the natural one (αes = αet) (Figure 4.14a).
A few remarks in Figure 4.14 are in order
• The actual value of q for each phase under neighboring poles is 2 and 1, respectively, to give an average of 3/2
• Due to the periodicity of two poles (2τ), the mmf distribution does not show fractional harmonics (ν<1 )
• There are both odd and even harmonics, as the positive and negative polarities of mmf (Figure 4.14c) are not fully symmetric
• Due to a two pole periodicity we may have a = 1 (Figure 4.14d), or a = 2, 4
• The chording and distribution (spread) factors (Ky1, Kq1) for the fundamental may be determined from Figure 4.14e using simple phasor composition operations.
This is a kind of general method valid both for integer and fractional q.
Extracting the fundamental and the space harmonics of the mmf distribution (Figure 4.14c) takes implicit care of these factors both for the fundamental and for the harmonics.