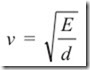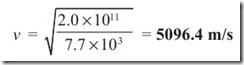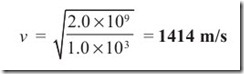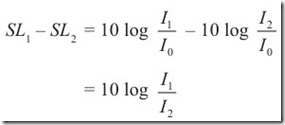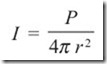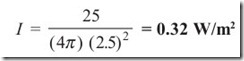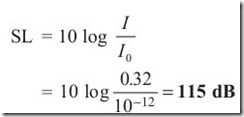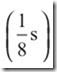WAVE MOTION
In all our activities, the availability of energy is a continuous problem. The conversion of energy into a useful form and the transportation of this energy from the point of conversion to the point of use are matters of immediate concern. In different communication procedures the message is carried through the motion of waves or through the motion of matter (particles). Waves enable the transfer of energy from one point to another without the physical transfer of matter between the points. Sounds reach our ears by means of air waves. Radio signals are waves that transmit music or speech. All waves have certain properties in common that will now be discussed.
MECHANICAL WAVES
Energy and momentum can be transported from one place to another through the motion of particles. Wave motion provides an alternative way for transfer of energy and momentum without the movement of the material particles.
Water waves and sound waves, for example, are mechanical waves, that travel through a deformable or elastic medium. They originate when some portion of the medium is displaced from its normal position and released.
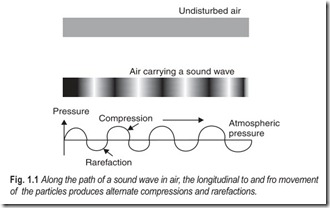
As a wave reaches a particle in the medium, Fig. 1.1, it sets that particle into motion and displaces it, thus transferring both kinetic and potential energy to it. We can regard the particles of the medium as moving only by small distances about their previous position,without undergoing any net overall displacement in the direction of the wave.
TYPES OF WAVES
Waves can be classified according to their broad physical properties; according to how the direction of motion of the particles is related to the direction of propagation of the wave; according to the number of dimensions in which they propagate energy and also according to how the particles of the medium move in time.
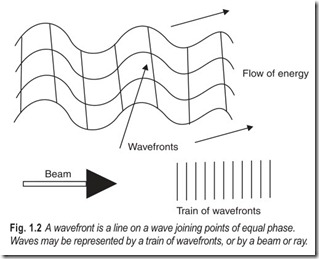
Imagine a stone is dropped in a still lake. Circular ripples spread out from the point where the stone entered the water. Along a given circular ripple, all points are in the same state of motion. These points define a surface called wavefront. If the medium is of uniform density, the direction of motion of the wave is at right angles to the wavefront. A line normal to the wavefront, indicating the direction of motion of the wave is called a ray, Fig. 1.2.
As a rule, the energy exerted by a wave flows at right angles to the wavefront, and it is sometimes simpler to represent the direction in which energy is flowing by means of straight lines bounding the wavefronts, that is, by means of a single straight line, representing a ray. This is a simplified representation of wave motion.
LONGITUDINAL WAVES
The different kinds of waves have many features in common. Having considered one type of wave, we can apply the same methods to describe the behaviour of other waves, such as sound waves, light waves.
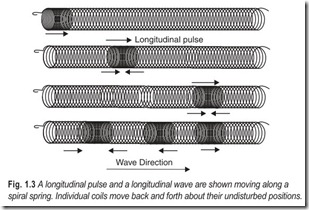
Waves in which the vibration of particles is in the same direction in which the wave travels are called longitudinal waves. Waves in which the movement of particles is at right angles to the direction in which the wave travels are called transverse waves.
Each particle on the path of a longitudinal wave, Fig. 1.3, performs simple harmonic motion about its average position as the wave moves through it. Although both types of wave may pass through the same material, their velocities are generally different because of the different physical properties of the material involved in propagating them.
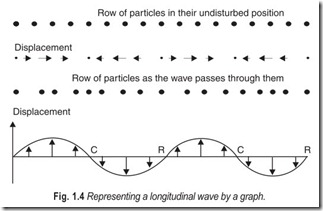
If we plot the displacement as ordinate against the horizontal equilibrium position of the particles we obtain the familiar sinusoidal graph, Fig. 1.4.A complete wavelength includes a compression and a rarefaction. The instantaneously disturbed particles are at the centre of the compressions and rarefactions.
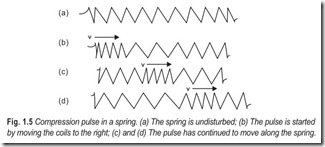
Let us considering a stretched spring. In Fig. 1.5 (a) the lines represent the position of the coils of the spring when the spring is undisturbed. A harmonic longitudinal wave can be set up in the spring if the end is moved with simple harmonic motion in a line parallel to the spring. The spring is compressed when the end is to the right of its normal position but expanded when the end is to the left of the normal. The result is that, as the end is moved in SHM, a harmonic succession of compressions and following expansions will move along the spring.
Longitudinal waves do not require shearing stress and hence may be transmitted through an elastic medium. The derivation of the relation between the speed of longitudinal waves and the properties of the medium is somewhat involved, only the end result is given.
where E is the appropriate modulus and d is the density. For a rod, E is the Young’s modulus; for a fluid, E is the bulk modulus B.
Example 1.1 Find the velocity of a compressional wave in an iron whose density is 7.7 × 103 kg/m3 and whose Young’s modulus is 2.0 × 1011 N/m2.
Solution
Example 1.2 Find the velocity of a longitudinal wave in water. B = 2.0 × 109 N/m and d = 1.0 × 103 kg m3 .
Solution
WAVE PROPERTIES
Waves travel with a definite speed through a uniform medium. Also, if we watch a single spot, we see that the waves pass the spot at regular intervals of time. In wave motion, factors such as wave speed, frequency, phase, wavelength and amplitude must be considered.
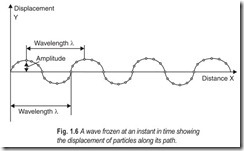
The speed of a wave is the distance it advances in unit time. The number of waves that pass a point per unit time is the frequency of the wave motion. The time required for a single wave to pass is called the time period T of the wave motion. The wavelength λ is the distance between two adjacent particles that are in the same phase. The amplitude A of the wave is the maximum displacement of the particle from its equilibrium position. A wavefront is a surface that passes through all points in the wave that are in the same phase. In a medium in which the speed is same in all directions, the wavefront is perpendicular to the direction that the wave travels. If the wave passes from one medium into another, the speed changes. In this process the frequency remains the same but the wavelength will change in proportion to the speed. If v increases, λ also increases.
If the energy which causes the disturbance carries on producing recurrent complete vibrations, then a continuous periodic wave is generated. We can form an accurate picture of such a wave by plotting the position, at one instant in time, of each particle in its path, Fig. 1.6. The distance between the wave crests or between the corresponding points on the curve is the wavelength.
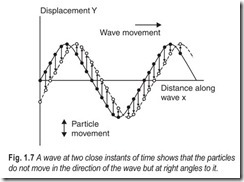
As the wave profile moves, it displaces the position of each particle on its path. All the particles on the wave vibrate with SHM but each one lags slightly behind the one on its left because of its inertia. Fig. 1.7 shows two positions of a wave separated by a short time interval. The wave profile moves from left to right but note that each particle moves up and down about its equilibrium position.
i.e. velocity = frequency × wavelength
v = nλ … (1.2)
ENERGY DISSIPATION AND WAVE MOTION
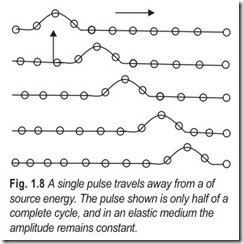
The energy supplied at a point of disturbance is transmitted to adjacent particles by the forces between the particles. If there is internal friction or damping, the energy travels away from the point in the form of a pulse. If the pulse continues to travel in direction, like a ripple on a piece of rope, each particle in its path will, in turn, assume the movement of the original particle as shown in Fig. 1.8.
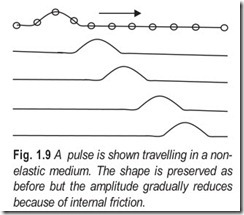
If the external friction is considered, the kinetic energy of the pulse will be converted to heat in a short distance, Fig. 1.9.
Example 1.3 One end of a rope is vibrated at 8 Hz and the waves generated measure 60 cm from crest to crest. How fast do they travel and what is the period of vibration of any part of the rope?
Solution v = n λ = 8 × 0.6
= 4.8 m/s
If vt and v0 be the velocities of sound at t°C and 0°C respectively,
then
where Tt and T0 are absolute temperatures.
Thus the velocity of sound is directly proportional to the square root of the absolute temperature.
Example 1.4 Calculate the increases in the velocity of sound for 1°C rise in temperature, if the velocity of sound at 0°C is 332 m/s.
The speed of sound in different mediums is given in Table 1.1.
Table 1.1 The Speed of Sound
|
Medium |
Speed (m/s) |
|
|
Gases |
Air (0°C) |
331 |
|
Air (20°C) |
343 |
|
|
Helium |
965 |
|
|
Hydrogen |
1284 |
|
|
Liquids |
Water (0°C) |
1402 |
|
Water (20°C) |
1482 |
|
|
Sea water |
1522 |
|
|
Solids |
Steel |
5941 |
|
Granite |
6000 |
|
|
Aluminium |
6420 |
INTENSITY OF A WAVE
The intensity I or rate of flow of energy by wave motion through unit area of the medium in a direction perpendicular to the direction of propagation of the wave is given by
|
…(1.4) |
||
|
where |
f = frequency a = amplitude |
|
|
v = velocity of the wave d = density of the medium. |
If P is the power of an isotopic source of sound at a distance r, the intensity or loudness of sound.
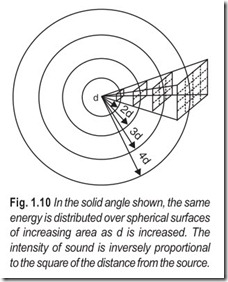
When a wave diverges in all directions from a source, the intensity reduces with the distance from the source according to an inverse square law. This is shown in Fig. 1.10.
It can be deduced from the above two relationships that the amplitude of a divergent ray falls off linearly with distance.
The intensity level is defined by an arbitrary scale that corresponds roughly to the sensation of loudness. Its unit is bel. A decibel is ![]() of a bel. This is taken as the standard unit.
of a bel. This is taken as the standard unit.
where I = intensity of sound and I0 = the weakest audible sound (10–12 W/m2)
SOUND LEVEL
The reference intensity level of 10–12 W/m2 is a typical value for the threshold of human hearing. A sound ofintensity I0 has a sound level of 0 dB, while a sound at the upper range of human hearing, called the threshold
of pain, has an intensity of 1 W/m2 and a sound level of 120 dB. Thus the human ear is capable of responding to intensities ranging over 12 orders of magnitude on a logarithmic scale of intensity called sound level, SL.
Example 1.5 The intensity of waves at a distance of 20 m from their source is 25 W/m2. What is the intensity at a distance of 50 m and how do the amplitudes of the waves compare at the two places?
The amplitudes are in the inverse ratio of the distances from the sources.
Each increase in intensity I by a multiplication factor 10 corresponds to adding 10 dB to the SL.We can also use dB as a relative measure to compare different sounds with one another rather than withthe reference intensity. Suppose we wish to compare two sounds of intensities I1 and I2 .
For example, two sounds whose intensity ratio is 2, differ in SL by 10 log 2 = 3 dB.
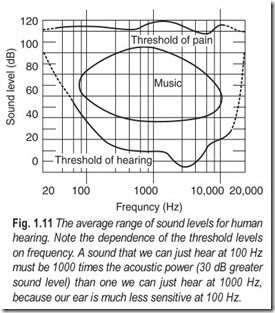
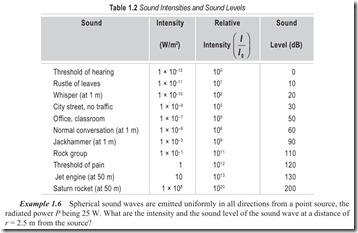
The sensitivity of the human ear varies with frequency. The threshold of 10–12 W/m2 applies only to the midrange frequencies around 1000 Hz. At the higher frequencies say 10,000 Hz, the threshold rises to about 10 dB (10–11 W/m2), while at lower frequencies, say 100 Hz the threshold is about 30 dB (10–9W/m2). It takes 1000 times the sound intensity at 100 Hz to produce the same physiological response as a given sound intensity at 1000 Hz. Fig. 1.11 shows the variation with frequency of the thresholds of hearing and pain and Table 1.2 shows some representative sound levels and their corresponding intensities.
Example 1.6 Spherical sound waves are emitted uniformly in all directions from a point source, the radiated power P being 25 W. What are the intensity and the sound level of the sound wave at a distance of r = 2.5 m from the source?
Solution All of the radiated power must pass through a sphere of radius r centered on the source. Thus
We see that the intensity of the sound drops off as the inverse square of the distance from the source. Thus
and
PROPERTIES OF SOUND WAVES
The properties of sound waves can be summed up as follows.
(i) Sound waves are longitudinal waves.
(ii) Sound travels through all states of matter.
(iii) The velocity of sound is maximum in solids and least in gases.
(iv) Sounds which can be heard by human beings are known as audible sounds. Their frequency range is from 20 to 20,000 Hz.
(v) Sounds of frequencies greater than 20,000 Hz are called ultrasonic sounds. Ultrasonic sounds can be received and emitted by bats.
(vi) Sounds of frequencies less than 20 Hz are called infrasonic sounds. Infrasonic sounds can be received by snakes.
(vii) Sound waves can be reflected.In the phenomenon of reflection, the speed, frequency and wavelength of the sound waves do not change.
(viii) Sound waves can be refracted. In the phenomenon of refraction, the frequency of the sound waves does not change but their velocity and wavelength change.
(ix) Sound waves exhibit the phenomenon of diffraction.
(xi) The normal level of sound is 60 dB to 120 dB.
(xii) Sound waves cannot travel through vacuum.
TRANSVERSE WAVES
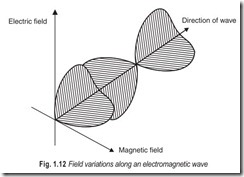
We are already familiar with the way in which light energy travels from a source to arrive essentially at some other point which it illuminates. What is happening in the region through which the light is passing? If it were possible to stop such a light wave and take measurements along its path, we would detect two influences— a fluctuating electric field at right angles to the direction of the beam and a fluctuating magnetic field at right angles both to the beam and the electric field (Fig. 1.12).
The electric field (E) and the magnetic field (H) have the same wavelength and they keep in phase. The energy of light is stored in these two fluctuating fields, the pattern of which is preserved as it travels along. In fact, electromagnetic waves may be produced by a vibrating charged particle, such as an electron, which creates a varying electric field.
REFRACTION OF WAVES
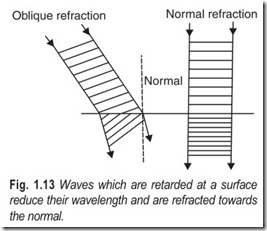
A change in medium or a change in conditions may cause a wave to slow down. This slowing down has the effect of shortening the wavelength, although the frequency of the wave remains the same. This is shown for normal incidence in Fig. 1.13, which also shows what happens when the wavefronts meet the surface obliquely. One end of each wavefront, the end which touches the obstacle first, slows up before the other and that whole wavefront is made to swing round. The retardation of the wave causes deviation towards the normal at the surface. Conversely, if the waves travel faster in the second medium, they deviate away from the normal. This phenomenon is called refraction.It may occursharplyor it may occurgradually.
REFLECTION OF WAVES
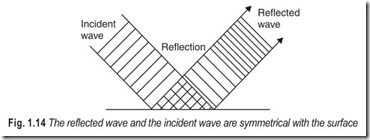
When a wave meets a surface separating two materials in which its velocity is different, some of the energy of the wave is reflected. The reflected wave has the same velocity, frequency and wavelength as the incident wave and the two waves are symmetrical with the surface, Fig. 1.14.
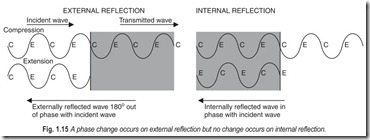
In some cases of reflection, a change of phase occurs which is of importance when considering the details of sound and light waves. In external reflection, the phase of a wave changes by 180°. In the case of internal reflection, the incident and reflected waves are in phase. This is shown in Fig. 1.15.
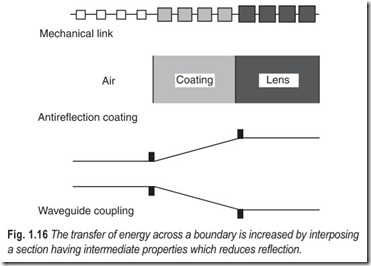
The greater the change in conditions at a surface, the greater is the fraction of energy reflected. When we want a wave to cross a boundary with minimum reflection, we try to reduce the abruptness of change. We do this in several ways, Fig. 1.16, depending on the kind of wave.
INTERFERENCE OF WAVES
When two or more waves combine at a particular point, they are said to interfere and the phenomenon is called interference. The resultant waveform is strongly dependent on the relative phases of the interfering waves.
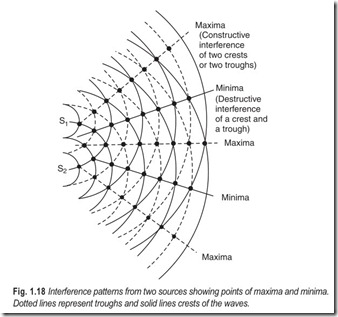
Figure 1.17 shows an example of occurrence of interference effects. The loudspeakers are driven from the same source. At points equidistant from the speakers (on the line AB, which represents the entire midplace) there is complete constructive interference if the speakers are driven in phase. There are also other points P where the waves arrive in phase and interfere constructively. These other points of constructive interference are located wherever the difference in distance to the speakers is a whole number of wavelengths.
At other points P, the differing distances x1 and x2 result in the waves possibly arriving at P out of phase, even if they started out in phase at the speakers. The listening environment might therefore have dead spots where partial or complete destructive interference occurs for a particular wavelengthλ. Maximum destructive interference occurs at points where
If the speakers emit a mixture of many different wavelengths some points P might show destructive interference of one wavelength and constructive intererence of another wavelength. The critical factor in determining the maxima and minima of sound intensity is the path difference x1 − x2 .
Interference is characteristic of wave motion and its appearance in any phenomenon testifies to the wave nature of that phenomenon.
In any interference pattern the amplitude varies in a regular manner. Since the intensity of the wave is proportional to the square of its amplitude we see that the rate of flow of energy is not distributed uniformly as in a single wave. In the interference pattern energy is diverted from the regions of destructive interference and appears at the regions of constructive interference, as shown in Fig. 1.18.
SUPERPOSITION OF WAVES
When two or more waves exist simultaneously in the same medium, each wave travels through the medium ignoring the presence of the other wave. In the sense of propagation through the medium neither wave affects the other. However, at a point where two waves of the same kind reach simultaneously, the medium will have a displacement that is the sum of the displacements of the individual waves. Here displacement refers to the departure from normal to that property of the medium which varies as the wave passes throughthe medium. If the property is a complex quantity, the sum is a vector sum. Let φ1 and φ2 represent thedisplacements of the individual waves. Then at every point in the medium and at each instant of time the resultant displacement is
φγ = φ1 + φ2 …(1.11)
COMPLEX WAVES
The waveforms which represent speech and telegraph signals are of complex shape. Nevertheless if they repeat the same pattern, complex waveforms can be analysed into two or more components each of which is itself of pure sine-waveform. Due to this reason, ac theory and transmission line theory have been developed on the assumption of a pure sine-waveform.
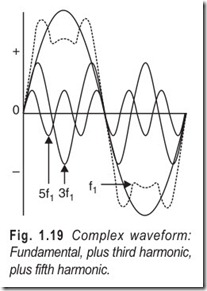
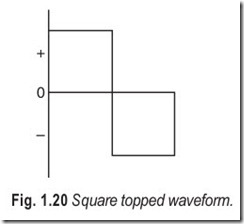
In any complex waveform the lowest frequency component is known as the fundamental frequency ; other sinusoidal components whose frequencies are exact multiples of the fundamental frequency are called harmonics. The first harmonic coincides with the fundamental frequency.A complex waveform containing fundamental frequency f1 , thirdharmonic frequency 3f1 and fifth harmonic frequency 5f1 is built up inFig. 1.19. This shows the general symmetrical waveform produced by the presence of odd harmonics and in the limit, if all odd harmonic frequencies upto infinity are taken, the square topped waveform of Fig. 1.20, originated by most forms of telegraph transmitters, is produced.
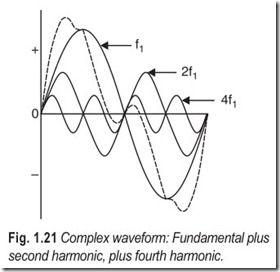
Complex waves which include even harmonics only are shown in Fig. 1.21 for the fourth harmonic, second harmonic and fundamental.
Harmonic components of a complex wave may differ from the fundamental in three ways: (i) in relative peak values, (ii) in frequency and (iii) in phase displacement. It will be noted that the complete complex wave or ‘group’ repeats its instantaneous values at the fundamental frequency.
The complete analysis of a complex wave is stated by Fourier’s Theorem: any complex wave which is a repeating function can be split into components each of which is a pure sine wave whose frequency is some whole-number multiple of the fundamental frequency.
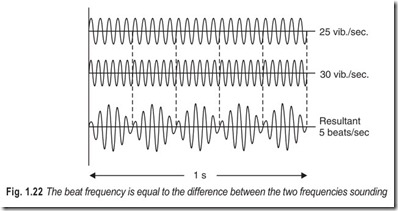
BEATS
The interference of two sound waves is also apparent when the frequency of one wave is near to that of the other. The interaction of the waves causes a periodic change in intensity (loudness) of the sound. This can be explained by adding graphically the amplitudes of the two waves at every instant of time, (Fig. 1.22). The resultant amplitude is maximum when the waves are in step and a minimum when they are out of step. If these frequencies differ by (say) five vibrations per second then the waves get in and out of step five times per second and the number of pulses or beats heard per second is five. In general
Beat frequency = f1 – f2 …(1.12)
Up to a beat frequency of 16 Hz, we hear a note of frequency intermediate between that of the two sources, waxing and waning in loudness. At beat frequencies above this we hear the two notes separately but they produce a disagreeable sound, which gets more dissonant as the beat frequency rises. Eventually the beat frequency itself is heard as a separate note. This plays an important part in harmony.
The effect is used to tune a piano string to the same frequency as that of the tuning fork, and to tune one string of a guitar with another. The tension of the string is varied until the beat frequency reduces to zero.
FORCED VIBRATIONS
When a vibrating tuning fork is held close to the ear the sound is heard quite loudly but the loudness falls off rapidly as the fork is moved away. Since the prongs are of very small area, we may regard the fork as an approximate point source of energy, and allowing for attenuation the loudness of the sound is inversely proportional to the square of the distance from the source. In this respect a point source of sound may be compared with a point source of electromagnetic waves. Both obey an inverse square law.
If, however, the stem of the fork is pressed against a table top, the sound can be heard clearly all over the room. Under these conditions the table is set into forced vibrations and then acts as a large extended source. It may then be considered as equivalent to a large number of point sources, all of which contribute to the loudness of the room at any point in the room.
Although the sound is louder, it does not last long. The amplitude of sound of the table top is very much less than that of the tuning fork, but its large area transfers energy to the air at a much greater rate than the small area of the prongs.
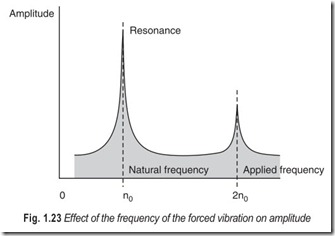
RESONANCE
The best way to set a child’s swing in motion is to give it small pushes in time with the natural period of the swing. This is an example of a general principal in physics called resonance.
Resonance is said to occur whenever a particular body or system is set into oscillation at its own natural frequency as a result of impulses received from some other system which is vibrating with the same frequency.
Under these conditions it is possible for a very large amplitude of vibrations to be set up.
We find applications of the same principle in other branches of physics. The action of tuning a radio set is to adjust the value of capacitance in a circuit until it has the same natural period of oscillation for electricity as that of incoming signal. The small emf set up in the aerial is then able to build up a similar emf of large amplitude in the tuned circuit.
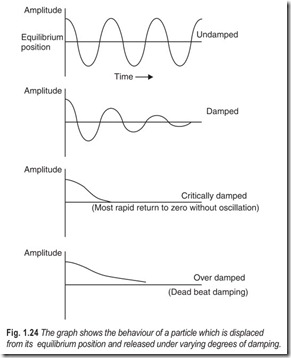
The tendency to resonate can be reduced by producing a means of absorbing the undesirable energy of vibration.
Instruments with moving pointers, such as balances and electrical meters, are damped to curtail oscillation about the final rest position. The damping may be provided by viscous, frictional, electrical or magnetic forces. It is important to provide just the right degree of damping. This is usually the damping which returns the system to equilibrium position in the shortest possible time without oscillation. The condition is called critical damping. Fig 1.24 illustrates the effect of varying degrees of damping.
ECHOES
Echoes are produced by the reflection of sound from a hard surface such as a wall or cliff.
Let us suppose that a person claps his hands when standing some distance from a high wall and listens for the echo. The time which elapses before the echo arrives will depend on the distance from the wall. In order that the echo may be heard separately from the original clap it must arrive at least 0.1 second later. Since sound travels at about 330 m/s, the reflected wave must have travelled a total distance of at least 33 m. Consequently, the minimum distance of the wall must be about 17m.
When the reflecting surface is less than this distance the echo follows so closely upon direct sound wave that they cannot be distinguished as separate sounds. One merely receives the impression that the original sound has been prolonged. This effect is called reverberation.
Descriptive Questions
1. Describe the primary difference between longitudinal and transverse waves.
2. What possible changes could occur to the velocity, frequency and wavelength of a wave as it goes from one medium to another?
3. What is the difference between progressive and standing waves?
4. What decides whether a medium will transmit longitudinal or transverse waves?
5. When transverse waves travel along a rope, each particle moves only at right angles to the rope. What is it that moves along the rope?
6. Why are waves of various kinds so useful in conveying information from one place to another?
7. Suggest practical uses that can be made of the fact that sound waves travel through solids with greater ease than through liquids or gases.
8. A sound produced by a tuning fork can be greatly amplified if the base of the vibrating fork is held against the top of a table. Explain why this happens.
9. What fundamental condition must exist for an object to resonate when a sound wave falls on it?
10. Explain why sound will not travel through vacuum.
11. Give some examples of the role that resonance plays in musical instruments. Under what circumstances should resonance be avoided in these instruments?
12. How are beats useful in tuning a musical instrument?
13. Justify the statements that the speed of sound in air increases by about 0.61 m/s for each centigrade degree rise in temperature from 0°C.
14. Explain the laws of reflection of sound and explain how an echo may be produced.
15. Explain the difference between longitudinal and transverse waves. State a practical example of each type.
Account for the fact that a distant lightening flash is seen before the thunder is heard.
16. State two essential differences between the modes of propagation of sound and light waves.
Multiple Choice Questions
1. Which of the following is transmitted by a wave?
(a) amplitude (b) velocity
(c) energy (d) momentum
2. It is possible to distinguish between transverse and longitudinal waves by studying the property of
(a) interference (b) diffraction
(c) reflection (d) polarisation
3. The relation between frequency n, wavelength λ, and velocity of propagation v of the wave is
(a) v = nλ (b) λ = nv
4. The wavelength of sound is 10 cm. Its frequency is
(a) 3.3 kHz (b) 3.3 MHz
(c) 330 Hz (d) 33 Hz
5. Sound waves having the following frequencies are audible to human beings. (a) 5 Hz (b) 27,000 Hz
(c) 5,000 Hz (d) 50,000 Hz
6. The velocity of sound is largest in
(a) air (b) water
(c) steel (d) vacuum
Fill in the Blanks
1. A wave is a ……………………………………….that travels through a medium.
2. ………………………………………. may be transmitted by waves.
3. Where the waves arrive out of phase the interference is called ………………………………………..
4. Wavelength λ is the distance between two adjacent particles that are in the………………………………………..
5. For resonance there is a………………………………………. transfer of energy and a resultant sound.
6. In air, at ordinary temperature, the speed of sound is approximately………………………………………..
7. The speed of sound in any medium depends on the ……………………………………….of the medium and upon its.
8. A sound wave may be………………………………………. if the speed of the wave is not the same in all parts of the medium.
9. An……………………………………….occurs when reflected sound waves return to the observer in 0.1s or more after the original reaches him.
10. The intensity level is defined by an arbitrary scale that corresponds roughly to the of………………………………………..
Numerical Questions
1. What is the wavelength of a radio station broadcasting at 1,000 Hz frequency? Speed of radio waves is equal to 3 × 108 m/s. (300 m)
2. Assume that Young’s modulus for silver is 7.75 × 1010 N/m2 at 20°C. If it has a density of 1.05 × 103 kg/m3, how fast does sound travel through silver? (2.67 × 103 m/s)
3. Copper has a density of 9 g/cm3 and a bulk modulus of 1.2 × 1011 N/m2. What is the speed of a wave through it? (3.6 × 103 m/s)
4. A person standing 99 m from the foot of a tall cliff claps his hands and hears an echo 0.6 s later. Calculate the velocity of sound in air. (330 m/s)
5. What are the wave lengths in air of the piano’s lowest note (frequency 27.5 Hz) and its highest (frequency 4,186 Hz)? Speed of sound is equal to 330 m/s. (12 m; 7.9 cm)
6. A car, sounding its horn at a frequency of 256 Hz, approaches a wall and the echo from the wall has a frequency of 288 Hz. How fast is the car moving? (speed of sound = 330 m/s.) (19.4 m/s)
7. Two closed organ pipes are 785 and 80 cm long. What is the frequency of the beats produced between their fundamental tones? (Speed of sound = 330 m/s). (2 beats/s)
8. Two waves of the same frequency but of amplitude in the ratio 1 : 3 are superposed. What is the ratio of maximum to minimum intensity? (4:1)
9. Two tuning forks of frequencies 512 Hz and 520 Hz are sounded together. What is the time interval between the maximum sound and the minimum sound?
ANSWERS
Multiple Choice Questions
1. (c) & (d) 2. (d) 3. (c) 4. (a) 5. (c) 6. (c)
Fill in the Blanks |
||
|
1. disturbance 4. same phase 7. elastic constants, density |
2. energy and momentum 5. rapid, louder 8. reflected |
3. destructive interference 6. 343 m/s 9. echo, sound |
10. threshold, hearing