Alternators:Synchronous Reactance

Synchronous Reactance

From the above discussion, it is clear that for the same field excitation, terminal voltage is decreased from its no-load value E0 to V (for a lagging power factor). This is because of

1. drop due to armature resistance, IRa

2. drop due to leakage reactance, IXL

3. drop due to armature reaction.

The drop in voltage due to armature reaction may be accounted for by assumiung the presence of a fictitious reactance Xa in the armature winding. The value of Xa is such that IXa represents the voltage drop due to armature reaction.

The leakage reactance XL (or XP) and the armature reactance Xa may be combined to give synchronous reactance XS.

Hence XS = XL + Xa*

Therefore, total voltage drop in an alternator

under load is = IRa + jIXS = I(Ra + jXS) = IZS where ZS is known as synchronous impedance of the armature, the word ‘synchronous’ being used merely as an indication that it refers to the working conditions.

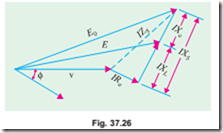
Hence, we learn that the vector difference between no-load voltage E0 and terminal voltage V is equal to IZS, as shown in Fig. 37.26.

Vector Diagrams of a Loaded Alternator

Before discussing the diagrams, following symbols should be clearly kept in mind.

E0 = No-load e.m.f. This being the voltage induced in armature in the absence of three factors discussed in Art. 37.16. Hence, it represents the maximum value of the induced e.m.f.

E = Load induced e.m.f. It is the induced e.m.f. after allowing for armature reaction. E is vectorially less than E0 by IXa. Sometimes, it is written as Ea (Ex. 37.16).

In Fig. 37.27 (a) is shown the case for unity p.f., in Fig. 37.27 (b) for lagging p.f. and in Fig. 37.27 (c) for leading p.f. All these diagrams apply to one phase of a 3-phase machine. Diagrams for the other phases can also be drawn similary.

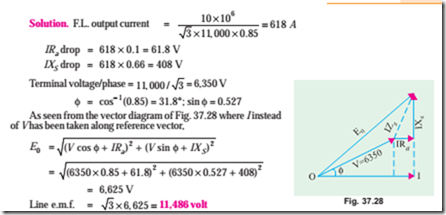
Example 37.16. A 3-phase, star-connected alternator supplies a load of 10 MW at p.f. 0.85 lagging and at 11 kV (terminal voltage). Its resistance is 0.1 ohm per phase and synchronous reactance 0.66 ohm per phase. Calculate the line value of e.m.f. generated.