THE DOUBLE CAGE BEHAVES LIKE A DEEP BAR CAGE

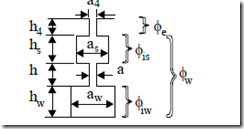
In some applications, very high starting torque–T_start/T_rated ≥ 2.0–is required. In such cases, a double cage is used. It has been proved that it behaves like a deep bar cage, but it produces even higher starting torque at lower starting current. For the case when skin effect can be neglected in both cages, let us consider a double cage as configured in Figure 9.18. [8]

 

 

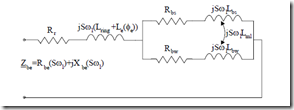
Figure 9.18 Double cage rectangular-shape geometry a.) and equivalent circuit b.)

The equivalent single bar circuit is given in Figure 9.18b. For the common ring of the two cages

Rr = Rring, Rbs = Rbs upper bar, Rbw = Rbw lower bar (9.49) For separate rings

Rr = 0, Rbs = Rbs + Rerings, Rbw = Rbw + Reringw (9.50)

The ring segments are included into the bar resistance after approximate reduction as shown in Chapter 6. The value of L_ring is the common ring inductance or is zero for separate rings. Also for both cases, L_e(Φ_e) refers to the slot neck flux.

Le (Φe )= µ0lstack ha44 (9.51)

We may add into L_e the differential leakage inductance of the rotor. The start (upper) and work (lower) cage inductances L_bs and L_bw include the end ring inductances only for separate rings. Otherwise, the bar inductances are

Lbs = µ0lstack 3ha^s_s

Lbw = µ0lstack ^ 3ha_{ww +} ha ₊ ha_ss _ (9.52) There is also a flux common to the two cages represented by the flux in the starting cage. [3]

Lml = µ0lstack 2hass (9.53)

In general, L_ml is neglected though it is not a problem to consider in solving the equivalent circuit in Figure 9.18. It is evident (Figure 9.18a) that the starting (upper) cage has a large resistance (R_bs) and a small slot leakage inductance L_bs, while for the working cage the opposite is true.

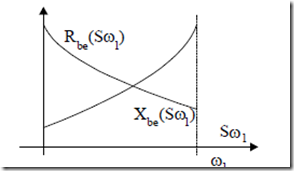
Consequently, at high slip frequency, the rotor current resides mainly in the upper (starting) cage while, at low slip frequency, the current flows mainly into the working (lower) cage. Thus both R_be and X_be vary with slip frequency as they do in a deep bar single cage (Figure 9.19).

Figure 9.19 Equivalent parameters of double cage versus slip frequency 

LEAKAGE FLUX PATH SATURATION–A SIMPLIFIED APPROACH

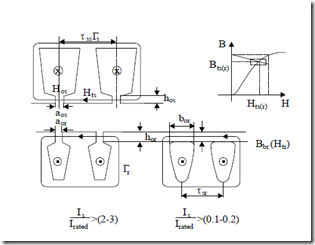
Leakage flux path saturation occurs mainly in the slot necks zone for semiclosed slots for currents above 2 to 3 times rated current or in the rotor slot iron bridges for closed slots even well below the rated current (Figure 9.20).

Consequently,

a ‘os = aos + (τss µ−saos )µ0; τss = πNDsi

a ‘or aor + sr µraor )µ0; τsr = π(DNi −s 2g) (9.54) (τ −

= a ‘or = b_µor_brµb

The slot neck geometrical permeances will be changed to: a′_os/h_os, a′_or/h_or, or a′_or/h_or dependent on stator (rotor) current.

Figure 9.20 Leakage flux path saturation conditions

With n_s the number of turns (conductors) per slot, and I_s and I_b the stator and rotor currents, the Ampere’s law on Γ_s, Γ_r trajectories in Figure 9.20 yields

Hts (τss − aos )+ H aos os ≈ n Is s 2; µsHts = Bts = µ0Hos

Htr (τsr − aor )+ H aor or ≈ Ib 2; µrHtr = Btr = µ0Hor (9.55)

H btr or = Ib 2; µbr = HBtbtb

The relationship between the equivalent rotor current I_r′ (reduced to the stator) and I_b is (Chapter 8)

Ib = I ‘r 6p1qnNsrKw1 = I ‘n Kr s w1 NNsr (9.56)

N_s–number of stator slots; K_w1–stator winding factor.

When the stator and rotor currents I_s and I_r′ are assigned pertinent values, iteratively, using the lamination magnetization curves, Equations (9.55) may be solved (Figure 9.20) to find the iron permeabilities of teeth tops or of closed rotor slot bridges. Finally, from (9.54), the corrected slot openings are found. With these values, the stator and rotor parameters (resistances and leakage inductances) as influenced by the skin effect (in the slot body zone) and by the leakage saturation (in the slot neck permeance) are recalculated. Continuing with these values, from the equivalent circuit, new values of stator and rotor currents I_s, I_r′ are calculated for given stator and voltage, frequency and slip. The iteration cycles continue until sufficient convergence is obtained for stator current.

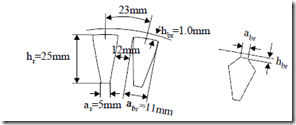
Example 9.4. An induction motor has semiclosed rectangular slots whose geometry is shown in Figure 9.21.

The current density design for rated current is j_Co = 6.5 A/mm² and the slot fill factor K_fill = 0.45. The starting current is 6 times rated current. Let us calculate the slot leakage specific permeance at rated current and at start.

Solution

The slot mmf n_sI_s is obtained from

n I_{s s} = (h a K_{s s} ) _{fill Co}j =10 35⋅ ⋅0.45⋅6.5 =1023.75Ampereturns

Making use of (9.54),

H_ts (18− 4.5)^{+ B}_µ^ts0 4.5^_ ⋅10⁻³ =1023.75 2

Bts ts = − H 3ts µ0

It is very clear that for rated current B_ts < 0.4029, so the tooth heads are not saturated. In (9.54), a_os′ = a_os and the slot specific geometrical permeance λ_s is

⋅

3⋅10 4.5+10 4.5

For the starting conditions,

Htstart (18− 4.5)⋅10−3 + Bµ0ts 4.5 ⋅10−3 = 6142.5 2

Btstart = 2.41− Htstart 3µ0

Now we need the lamination magnetization curve. If we do so we get B_tstart

≈ 2.16T, H_tstart ≈ 70,000 A/m. The iron permeability µ_s is

µs = Btstart µ0−1 = 70000⋅2.1.16256 10⋅ −6 = 24.56

µ0 Htstart

Consequently, aos ‘= aos + (τ −s µsaos )µ =0 4.5+ (1824−.564.5) = 5.05mm

The slot geometric specific permeance is, at start,

⋅

The leakage saturation of tooth heads at start is not very important in our case. In reality, it could be more important for semiclosed stator (rotor) slots.

Example 9.5. Let us consider a rotor bar with the geometry of Figure 9.21. The bar current at rated current density j_Alr = 6.0 A/mm² is

Ibr = jAlrhr A

 

Figure 9.22. Closed rotor slots

Calculate the rotor bridge flux density for 10%, 20%, 30%, 50%, 100% of rated current and the corresponding slot geometrical specific permeance.

Solution

Let us first introduce a typical magnetization curve.

B(T)	0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5
H(A/m)	22.8	35	45	49	57	65	70	76	83	90
B(T)	0.55	0.6	0.65	0.7	0.75	0.8	0.85	0.9	0.95	1
H(A/m)	98	106	115	124	135	148	162	177	198	220

B(T)	1.05	1.1	1.15	1.2	1.25	1.3	1.35	1.4	1.45	1.5
H(A/m)	237	273	310	356	417	482	585	760	1050	1340
B(T)	1.55	1.6	1.65	1.7	1.75	1.8	1.85	1.9	1.95	2.0
H(A/m)	1760	2460	3460	4800	6160			8270 11170 15220 22000 34000

Neglecting the tooth top saturation and including only the bridge zone, the Ampere’s law yields

= I ;b H br = aIbrb ; a br =11mm

H br a br

For various levels of bar current, H_br and B_br become

Ib (A)	120	240	360	600	1200
Hbr	10909	21818	32727	54545	109090
Bbr	1.84	1.95	1.98	2.1	2.2
µ µrel = µbr0	134.28	71.16	48.165	30.653	16.056
aor ‘= µarelbr (mm)	0.0819	0.1546	0.2284	0.3588	0.6851
λslot = 3(a r2+hrabr ) + ahorbr‘	14.293	75.1	5.42	3.8287	2.5013

Note that at low current levels the slot geometrical specific permeance is unusually high. This is because the iron bridge is long (a_br = 11mm); so H_br is small at small currents.

Also, the iron bridge is 1mm thick in our case, while 0.5 to 0.6 mm would produce better results (lower λ_slot). The slot height is quite large (h_r = 25 mm) so significant skin effect is expected at high slips. We investigated here only the currents below the rated one so Sf₁ < 3 Hz in general. Should the skin effect occur, it would have reduced the first term in λ_slot (slot body specific geometrical permeance) by the factor K_x.

As a conclusion to this numerical example, we may infer that a thinner bridge with a smaller length would saturate sooner (at smaller currents below the rated one), producing finally a lower slot leakage permeance λ_slot. The advantages of closed slots are related to lower stray load losses and lower noise.