microcontrollers

THE INSTRUCTION SET ARCHITECTURE

In this chapter we tackle a central topic in computer architecture: the language understood by the computer’s hardware, referred to as its machine language. The machine language is usually discussed in terms of its assembly language, which is functionally equivalent to the corresponding machine language except that the assembly language uses more intuitive names such as Move, Add, and Jump instead of the actual binary words of the language. (Programmers find constructs such as “Add r0, r1, r2” to be more easily understood and rendered with- out error than 0110101110101101.)

We begin by describing the Instruction Set Architecture (ISA) view of the machine and its operations. The ISA view corresponds to the Assembly Language/Machine Code level described in Figure 1-4: it is between the High Level Language view, where little or none of the machine hardware is visible or of concern, and the Control level, where machine instructions are interpreted as register transfer actions, at the Functional Unit level.

In order to describe the nature of assembly language and assembly language programming, we choose as a model architecture the ARC machine, which is a simplification of the commercial SPARC architecture common to Sun computers. (Additional architectural models are covered in The Computer Architecture Companion volume.)

We illustrate the utility of the various instruction classes with practical examples of assembly language programming, and we conclude with a Case Study of the Java bytecodes as an example of a common, portable assembly language that can be implemented using the native language of another machine.

Hardware Components of the Instruction Set Arc hitecture

The ISA of a computer presents the assembly language programmer with a view of the machine that includes all the programmer-accessible hardware, and the instructions that manipulate data within the hardware. In this section we look at the hardware components as viewed by the assembly language programmer. We begin with a discussion of the system as a whole: the CPU interacting with its internal (main) memory and performing input and output with the outside world.

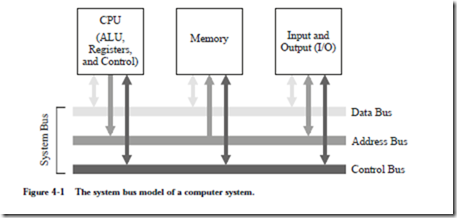
THE SYSTEM BUS MODEL REVISITED

Figure 4-1 revisits the system bus model that was introduced in Chapter 1.

The purpose of the bus is to reduce the number of interconnections between the CPU and its subsystems. Rather than have separate communication paths between memory and each I/O device, the CPU is interconnected with its memory and I/O systems via a shared system bus. In more complex systems there may be separate busses between the CPU and memory and CPU and I/O.

Not all of the components are connected to the system bus in the same way. The CPU generates addresses that are placed onto the address bus, and the memory receives addresses from the address bus. The memory never generates addresses, and the CPU never receives addresses, and so there are no corresponding connections in those directions.

In a typical scenario, a user writes a high level program, which a compiler translates into assembly language. An assembler then translates the assembly language program into machine code, which is stored on a disk. Prior to execution, the machine code program is loaded from the disk into the main memory by an operating system.

During program execution, each instruction is brought into the ALU from the memory, one instruction at a time, along with any data that is needed to execute the instruction. The output of the program is placed on a device such as a video display, or a disk. All of these operations are orchestrated by a control unit, which we will explore in detail in Chapter 6. Communication among the three components (CPU, Memory, and I/O) is handled with busses.

An important consideration is that the instructions are executed inside of the ALU, even though all of the instructions and data are initially stored in the memory. This means that instructions and data must be loaded from the memory into the ALU registers, and results must be stored back to the memory from the ALU registers.

MEMORY

Computer memory consists of a collection of consecutively numbered (addressed) registers, each one of which normally holds one byte. A byte is a col- lection of eight bits (sometimes referred to by those in the computer communications community as an octet). Each register has an address, referred to as a memory location. A nibble, or nybble, as it is sometimes spelled, refers to a col- lection of four adjacent bits. The meanings of the terms “bit,” “byte,” and “nibble” are generally agreed upon regardless of the specifics of an architecture, but the meaning of word depends upon the particular processor. Typical word sizes are 16, 32, 64, and 128 bits, with the 32-bit word size being the common form for ordinary computers these days, and the 64-bit word growing in popularity. In this text, words will be assumed to be 32-bits wide unless otherwise specified. A comparison of these data types is shown in Figure 4-2.

In a byte-addressable machine, the smallest object that can be referenced in memory is the byte, however, there are usually instructions that read and write multi-byte words. Multi-byte words are stored as a sequence of bytes, addressed by the byte of the word that has the lowest address. Most machines today have instructions that can access bytes, half-words, words, and double-words.

When multi-byte words are used, there are two choices about the order in which the bytes are stored in memory: most significant byte at lowest address, referred

to as big-endian, or least significant byte stored at lowest address, referred to as little-endian. The term “endian” comes from the issue of whether eggs should be broken on the big or little end, which caused a war by bickering politicians in Jonathan Swift’s Gulliver’s Travels. Examples of big and little-endian formats for a 4-byte, 32-bit word is illustrated in Figure 4-3.

The bytes in a multi-byte word are stored at consecutive addresses, as shown in Figure 4-3. In a byte-addressable memory each byte is accessed by its specific address. The 4-byte word is accessed by referencing the address of the byte with the lowest address, x in Figure 4-3. This is true regardless of whether it is big-endian or little-endian. Since addresses are counted in sequence beginning with zero, the highest address is one less than the size of the memory. The highest address for a 232 byte memory is 232–1. The lowest address is 0.

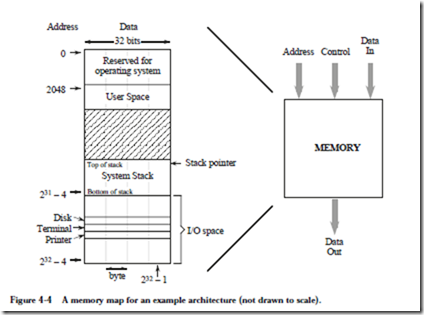
The example memory that we will use for the remainder of the chapter is shown in Figure 4-4. This memory has a 32-bit address space, which means that a pro- gram can access a byte of memory anywhere in the range from 0 to 232 – 1. The address space for our example architecture is divided into distinct regions which are used for the operating system, input and output (I/O), user programs, and

the system stack, which comprise the memory map, as shown in Figure 4-3. The memory map differs from one implementation to another, which is partly why programs compiled for the same type of processor may not be compatible across systems.

The lower 211 = 2048 addresses of the memory map are reserved for use by the operating system. The user space is where a user’s assembled program is loaded, and can grow during operation from location 2048 until it meets up with the system stack. The system stack starts at location 231 – 4 and grows toward lower addresses. The portion of the address space between 231 and 232 – 1 is reserved for I/O devices. The memory map is thus not entirely composed of real memory, and in fact there may be large gaps where neither real memory nor I/O devices exist. Since I/O devices are treated like memory locations, ordinary memory read and write commands can be used for reading and writing devices. This is referred to as memory mapped I/O.

It is important to keep the distinction clear between what is an address and what is data. An address in this example memory is 32 bits wide, and a word is also 32 bits wide, but they are not the same thing. An address is a pointer to a memory location, which holds data.

In this chapter we assume that the computer’s memory is organized in a single address space. The term address space refers to the numerical range of memory addresses to which the CPU can refer. In Chapter 7 (Memory), we will see that there are other ways that memory can be organized, but for now, we assume that memory as seen by the CPU has a single range of addresses. What decides the size of that range? It is the size of a memory address that the CPU can place on the address bus during read and write operations. A memory address that is n bits wide can specify one of 2n items. This memory could be referred to as having an n-bit address space, or equivalently as having a (2n) byte address space. For exam- ple, a machine having a 32-bit address space will have a maximum capacity of 232 (4 GB) of memory. The memory addresses will range from 0 to 232- 1, which is 0 to 4,294,967,295 decimal, or in the easier to manipulate hexadecimal for- mat, from 00000000H to FFFFFFFFFH. (The ‘H’ indicates a hexadecimal number in many assembly languages.)

THE CPU

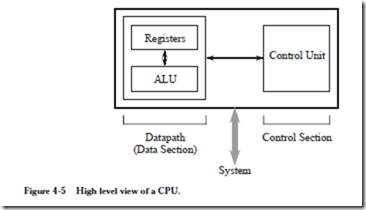
Now that we are familiar with the basic components of the system bus and memory, we are ready to explore the internals of the CPU. At a minimum, the CPU consists of a data section that contains registers and an ALU, and a control section, which interprets instructions and effects register transfers, as illustrated in Figure 4-5. The data section is also referred to as the datapath.

The control unit of a computer is responsible for executing the program instructions, which are stored in the main memory. (Here we will assume that the machine code is interpreted by the control unit one instruction at a time, though in Chapter 9 we shall see that many modern processors can process several

instructions simultaneously.) There are two registers that form the interface between the control unit and the data unit, known as the program counter (PC)† and the instruction register (IR). The PC contains the address of the instruction being executed. The instruction that is pointed to by the PC is fetched from the memory, and is stored in the IR where it is interpreted. The steps that the control unit carries out in executing a program are:

1) Fetch the next instruction to be executed from memory.

2) Decode the opcode.

3) Read operand(s) from main memory, if any.

4) Execute the instruction and store results.

5) Go to step 1.

This is known as the fetch-execute cycle.

The control unit is responsible for coordinating these different units in the execution of a computer program. It can be thought of as a form of a “computer within a computer” in the sense that it makes decisions as to how the rest of the machine behaves. We will treat the control unit in detail in Chapter 6.

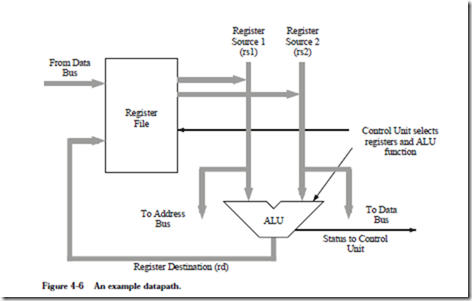
The datapath is made up of a collection of registers known as the register file and the arithmetic and logic unit (ALU), as shown in Figure 4-6. The figure depicts the datapath of an example processor we will use in the remainder of the chapter.

The register file in the figure can be thought of as a small, fast memory, separate from the system memory, which is used for temporary storage during computation. Typical sizes for a register file range from a few to a few thousand registers. Like the system memory, each register in the register file is assigned an address in sequence starting from zero. These register “addresses” are much smaller than main memory addresses: a register file containing 32 registers would have only a 5-bit address, for example. The major differences between the register file and the system memory is that the register file is contained within the CPU, and is there- fore much faster. An instruction that operates on data from the register file can often run ten times faster than the same instruction that operates on data in

memory. For this reason, register-intensive programs are faster than the equiva- lent memory intensive programs, even if it takes more register operations to do the same tasks that would require fewer operations with the operands located in memory.

Notice that there are several busses inside the datapath of Figure 4-6. Three busses connect the datapath to the system bus. This allows data to be transferred to and from main memory and the register file. Three additional busses connect the register file to the ALU. These busses allow two operands to be fetched from the register file simultaneously, which are operated on by the ALU, with the results returned to the register file.

The ALU implements a variety of binary (two-operand) and unary (one-operand) operations. Examples include add, and, not, or, and multiply. Operations and operands to be used during the operations are selected by the Control Unit. The two source operands are fetched from the register file onto busses labeled “Register Source 1 (rs1)” and “Register Source 2 (rs2).” The output from the ALU is placed on the bus labeled “Register Destination (rd),” where the results are conveyed back to the register file. In most systems these connections also include a path to the System Bus so that memory and devices can be accessed. This is shown as the three connections labeled “From Data Bus”, “To Data Bus”, and “To Address Bus.”

The Instruction Set

The instruction set is the collection of instructions that a processor can execute, and in effect, it defines the processor. The instruction sets for each processor type are completely different one from the other. They differ in the sizes of instructions, the kind of operations they allow, the type of operands they operate on, and the types of results they provide.This incompatibility in instruction sets is in stark contrast to the compatibility of higher level languages such as C, Pascal, and Ada. Programs written in these higher level languages can run almost unchanged on many different processors if they are re-compiled for the target processor.

(One exception to this incompatibility of machine languages is programs com- piled into Java bytecodes, which are a machine language for a virtual machine. They will run unchanged on any processor that is running the Java Virtual Machine. The Java Virtual Machine, written in the assembly language of the tar- get machine, intercepts each Java byte code and executes it as if it were running on a Java hardware (“real”) machine. See the Case Study at the end of the chapter for more details.)

Because of this incompatibility among instruction sets, computer systems are often identified by the type of CPU that is incorporated into the computer sys- tem. The instruction set determines the programs the system can execute and has a significant impact on performance. Programs compiled for an IBM PC (or compatible) system use the instruction set of an 80×86 CPU, where the ‘x’ is replaced with a digit that corresponds to the version, such as 80586, more commonly referred to as a Pentium processor. These programs will not run on an Apple Macintosh or an IBM RS6000 computer, since the Macintosh and IBM machines execute the instruction set of the Motorola PowerPC CPU. This does not mean that all computer systems that use the same CPU can execute the same programs, however. A PowerPC program written for the IBM RS6000 will not execute on the Macintosh without extensive modifications, however, because of differences in operating systems and I/O conventions.

We will cover one instruction set in detail later in the chapter.

Software for generating machine language programs

A compiler is a computer program that transforms programs written in a high-level language such as C, Pascal, or Fortran into machine language. Compilers for the same high level language generally have the same “front end,” the part that recognizes statements in the high-level language. They will have different “back ends,” however, one for each target processor. The compiler’s back end is responsible for generating machine code for a specific target processor. On the other hand, the same program, compiled by different C compilers for the same machine can produce different compiled programs for the same source code, as we will see.

In the process of compiling a program (referred to as the translation process), a high-level source program is transformed into assembly language, and the assembly language is then translated into machine code for the target machine by an assembler. These translations take place at compile time and assembly time, respectively. The resulting object program can be linked with other object pro- grams, at link time. The linked program, usually stored on a disk, is loaded into main memory, at load time, and executed by the CPU, at run time.

Although most code is written in high level languages, programmers may use assembly language for programs or fragments of programs that are time or space-critical. In addition, compilers may not be available for some special purpose processors, or their compilers may be inadequate to express the special operations which are required. In these cases also, the programmer may need to resort to programming in assembly language.

High level languages allow us to ignore the target computer architecture during coding. At the machine language level, however, the underlying architecture is the primary consideration. A program written in a high level language like C, Pascal, or Fortran may look the same and execute correctly after compilation on several different computer systems. The object code that the compiler produces for each machine, however, will be very different for each computer system, even if the systems use the same instruction set, such as programs compiled for the PowerPC but running on a Macintosh vs. running on an IBM RS6000.

Having discussed the system bus, main memory, and the CPU, we now examine details of a model instruction set, the ARC.

■ SUMMARY

Computer arithmetic can be carried out as we normally carry out decimal arithmetic by hand, while taking the base into account. A two’s complement or a ten’s complement representation is normally used for integers, whereas signed magnitude is normally used for fractions due to the difficulty of manipulating positive and negative fractions in a uniform manner.

Performance can be improved by skipping over 1’s in the Booth and bit-pair recoding techniques. An alternative method of improving performance is to use carryless addition, such as in residue arithmetic. Although carryless addition may be the fastest approach in terms of time complexity and circuit complexity, the more common weighted position codes are normally used in practice in order to simplify comparisons and represent fractions.

■ FURTHER READING

(Goldberg, 1990) is a concise but thorough source of numerous aspects of computer arithmetic. (Hamacher et al., 1990) provides a classic treatment of integer arithmetic. (Flynn, 1970) gives an early treatment of division by zero finding. (Garner, 1959) gives a complete description of the residue number system, whereas (Koren, 1993) gives a more tutorial treatment of the subject. (Huang and Goodman, 1979) describes how a memory based residue processor can be constructed. Koren (1993) also provides additional details on cascading carry-lookahead units. (Cochran, 1968) is a good source for the programming of the HP9100A calculator.

Cochran, D. S., “Internal Programming of the 9100A Calculator,” Hewlett-Pack- ard Journal, (Sept. 1968); Also see http://www.hpmuseum.org/jour- nals/9100:prg.htm.

Flynn, M. J., “On division by functional iteration,” IEEE Trans. Comp., C-19, no. 8, pp. 702-706, (Aug. 1970).

Garner, H. L., “The Residue Number System,” IRE Transactions on Electronic Computers, vol. 8, pp. 140-147, (Jun. 1959).

Goldberg, D., “Computer Arithmetic,” in Patterson, D. A. and J. L. Hennessy, Computer Architecture: A Quantitative Approach, 2/e, Morgan Kaufmann, (1995).

Hamacher, V. C., Z. G. Vranesic, and S. G. Zaky, Computer Organization, 3/e, McGraw Hill, (1990).

Huang, A. and J. W. Goodman, “Number Theoretic Processors, Optical and Electronic,” SPIE Optical Processing Systems, vol. 185, pp. 28-35, (1979).

Koren, I., Computer Arithmetic Algorithms, Prentice Hall, Englewood Cliffs, (1993).

■ PROBLEMS

3.1 Show the results of adding the following pairs of five-bit (i.e. one sign bit and four data bits) two’s complement numbers and indicate whether or not overflow occurs for each case:

3.2 One way to determine that overflow has occurred when adding two numbers is to detect that the result of adding two positive numbers is negative, or that the result of adding two negative numbers is positive. The overflow rules are different for subtraction: there is overflow if the result of subtracting a negative number from a positive number is negative or the result of subtracting a positive number from a negative number is positive.

Subtract the numbers shown below and determine whether or not an overflow has occurred. Do not form the two’s complement of the subtrahend and add: perform the subtraction bit by bit, showing the borrows generated at each position:

3.3 Add the following two’s complement and one’s complement binary numbers as indicated. For each case, indicate if there is overflow.

3.4 Show the process of serial unsigned multiplication for 1010 (multiplicand) multiplied by 0101 (multiplier). Use the form shown in Figure 3-12.

3.5 Show the process of serial unsigned multiplication for 11.1 (multiplicand) multiplied by 01.1 (multiplier) by treating the operands as integers. The result should be 101.01.

3.6 Show the process of serial unsigned division for 1010 divided by 0101.

Use the form shown in Figure 3-15.

3.7 Show the process of serial unsigned division for 1010 divided by 0100, but instead of generating a remainder, compute the fraction by continuing the process. That is, the result should be 10.12.

3.8 The equation used in Section 3.5.1 for c4 in a carry lookahead adder assumes that c0 is 0 for addition. If we perform subtraction by using the addition / subtraction unit shown in Figure 3-6, then c0 = 1. Rewrite the equation for c4 when c0 = 1.

3.9 The 16-bit adder shown below uses a ripple carry among four-bit carry lookahead adders.

(a) What is the longest gate delay through this adder?

(b) What is the shortest gate delay through this adder, from any input to any output?

(c) What is the gate delay for s12?

3.10 Use the Booth algorithm (not bit pair recoding) to multiply 010011 (multiplicand) by 011011 (multiplier).

3.11 Use bit pair recoding to multiply 010011 (multiplicand) by 011011 (mul- tiplier).

3.12 Compute the maximum gate delay through a 32-bit carry lookahead adder.

3.13 What is the maximum number of inputs for any logic gate in a 32-bit carry lookahead adder, using the scheme described in this chapter?

3.14 In a carry-select adder a carry is propagated from one adder stage to the next, similar to but not exactly the same as a carry lookahead adder. As with many other adders, the carry out of a carry-select adder stage is either 0 or 1. In a carry-select adder, two sums are computed in parallel for each adder stage: one sum assumes a carry-in of 0, and the other sum assumes a carry-in of 1.

The actual carry-in selects which of the two sums to use (with a MUX, for example). The basic layout is shown below for an eight-bit carry-select adder:

Assume that each four-bit adder (FBA) unit uses carry lookahead internally. Compare the number of gate delays needed to add two eight-bit numbers using FBA units in a carry-select configuration vs. using FBA units in which the carry is rippled from one FBA to the next.

(a) Draw a diagram of a functionally equivalent eight-bit carry lookahead configuration using the FBAs shown above.

(b) Show the number of gate delays for each adder configuration, by both the 8-bit carry-select adder shown above and the adder designed in part (a) above.

3.15 The path with the maximum gate delay through the array multiplier shown in Figure 3-22 starts in the top right PP element, then travels to the bottom row, then across to the left. The maximum gate delay through a PP element is three. How many gate delays are on the maximum gate delay path through an array multiplier that produces a p-bit result?

3.16 Given multiplication units that each produce a 16-bit unsigned product on two unsigned 8-bit inputs, and 16-bit adders that produce a 16-bit sum and a carry-out on two 16-bit inputs and a carry-in, connect these units so that the overall unit multiplies 16-bit unsigned numbers, producing a 32-bit result.

3.17 Using Newton’s iteration for division, we would like to obtain 32 bits of

precision. If we use a lookup table that provides eight bits of precision for the initial guess, how many iterations need to be applied?

3.18 Add (641)10 to (259)10 in unsigned BCD, using as few digits in the result as necessary.

3.19 Add (123)10 and (-178)10 in signed BCD, using four digit words.

Case Study: Calculator Arithmetic Using Binary Coded Decimal

Calculator arithmetic has traditionally been done in base 10, rather than in base 2. Calculators need to be small and inexpensive, and for that reason base 10 numbers are represented in binary coded decimal (BCD – see Chapter 2) using 4 bits per BCD digit, instead of using base 2 which would require a somewhat resource-intensive base conversion. A small 4-bit ALU can then do the computations in serial fashion, BCD digit by BCD digit.

THE HP9100A CALCULATOR

The popular HP9100A calculator, which came out in the late 1960’s, performed the basic arithmetic functions: addition, subtraction, multiplication, and division, as well as square root, ex, ln x, log x, trigonometric functions, and other functions, all using base 10 arithmetic. The HP9100A is actually a desktop calculator (see Figure 3-28), but was considered small for what it accomplished with

the technology of the day. The HP9100 display shows 10 significant digits, but all calculations are performed to 12 significant digits, with the two last significant digits (which are known as guard digits) being used for truncation and round-off errors. Although the HP9100A may seem like a relic today, the arithmetic methods are still relevant.

The next two sections describe general techniques for performing fixed point and floating point BCD addition and subtraction. Other calculator operations described in the remaining sections are performed in a similar manner, making use of the addition and subtraction operations.

BINARY CODED DECIMAL ADDITION AND SUBTRACTION

Consider adding (+255)10 and (+63)10 in BCD representation, as illustrated in Figure 3-29. Each base 10 digit occupies four bit positions, and addition is per- formed on a BCD digit by BCD digit basis (not bit by bit), from right to left, as we would normally carry it out by hand using a decimal representation. The result, (+318)10, is produced in BCD form as shown.

Subtraction in BCD is handled similar to the way subtraction is handled in two’s complement (adding the negative of the subtrahend) except that ten’s complement is used instead of two’s complement. Consider performing the subtraction operation (255 – 63 = 192)10. We can cast this into the addition problem (255 + (-63) = 192)10. We start by forming the nine’s complement of 63:

that the carry out of the highest digit position is discarded, as in two’s complement addition.

Unlike the two’s complement representation, we cannot simply look at the left- most bit to determine the sign. In ten’s complement, the number is positive if the leftmost digit is between 0 and 4, inclusive, and is negative otherwise. (The BCD bit patterns for 4 and 5 are 0100 and 0101, respectively, which both have a 0 in the leftmost bit, yet 4 indicates a positive number and 5 indicates a negative number.) If we use an excess 3 encoding for each digit, then the leftmost bit will indicate the sign. Figure 3-31 shows the encoding. Notice that six of the bit pat-

terns cannot occur, and so they are marked as don’t cares, ‘d’.

Now consider the design of a BCD full adder. The BCD full adder should sum two BCD digits and a carry-in, and should produce a sum BCD digit and a carry-out, all using excess 3. A design using two’s complement full adders is shown in Figure 3-32. The excess 3 BCD digits are added in the upper four two’s complement full adders (FAs). Since each operand is represented in excess 3, the result is in excess 6. In order to restore the result to excess 3, we need to subtract 3 from the result. As an alternative, we can add 13 to the result since 16 – 3 = 16 + 13 in a four-bit representation, discarding the carry out of the highest bit position. The latter approach is used in Figure 3-32, in which 1310 = 11012 is added to the result. Note that this only works if there is no carry. When there is a carry, then we need to also subtract 10 (or equivalently, add 6) from the result, besides subtracting 3 (or adding 13) to restore the excess 3 representation, and produce a

carry out. The approach taken here is to add 310 = 00112 for this situation, which has the same effect as adding (6 + 13) % 16 = 3, as shown in Figure 3-32.

In order to perform BCD subtraction, we can create a ten’s complement subtractor using base 10 full subtractors, as we did for the two’s complement subtractor described in Section 3.2.2. Alternatively, we can form the ten’s complement negative of the subtrahend, and then apply ordinary BCD addition. Figure 3-33

shows the computation (21 – 34 = -13)10 using the latter subtraction method for four-digit numbers. The ten’s complement negative of 34 is added to 21, which results in 9987 in ten’s complement, which is (-13)10 in signed magnitude.

BCD FLOATING POINT ADDITION AND SUBTRACTION

Consider a base 10 floating point representation with a two digit signed magnitude exponent and an eight digit signed magnitude fraction. On a calculator, a sample entry might look like:

which is in normalized form.

Now how is the number stored? A calculator user sees signed magnitude for both the exponent and the fraction, but internally, we might use a ten’s complement representation for both the exponent and the fraction. For the case above, the representation using ten’s complement would be: 88 for the exponent, and 62900000 for the fraction. Using an excess 3 representation in binary results in an exponent of 1011 1011 and a fraction of 1001 0101 1100 0011 0011 0011 0011 0011. Note that since we are using the leftmost bit for the sign, that the exponent range is [-50 to +49] and that the fraction range is [-.50000000 to +.49999999].

If we now try to represent +.9 in base 10, then we are again stuck because the leftmost bit of the fraction is used for a sign bit. That is, we cannot use 1100 in the most significant digit of the fraction, because although that is the excess 3 representation of 9, it makes the fraction appear negative. Here is a better solution: Just use ten’s complement for base 10 integer arithmetic, such as for exponents, and use signed magnitude for fractions.

Here is the summary thus far: we use a ten’s complement representation for the exponent since it is an integer, and we use a base 10 signed magnitude representation for the fraction. A separate sign bit is maintained for the fraction, so that each digit can take on any of the 10 values 0–9 (except for the first digit, which cannot be a zero) and so we can now represent +.9. We should also represent the exponent in excess 50 to make comparisons easier. The example above now looks like this internally, still in excess 3 binary form, with a two digit excess 50 exponent:

In order to add two numbers in this representation, we just go through the same steps that we did for the base 2 floating point representation described earlier. We start by adjusting the exponent and fraction of the smaller operand until the exponents of both operands are the same. If the difference in exponents is so great that the fraction of the smaller operand is shifted all the way to the right, then the smaller operand is treated as 0. After adjusting the smaller fraction, we convert either or both operands from signed magnitude to ten’s complement according to whether we are adding or subtracting, and whether the operands are positive or negative. Note that this will work now because we can treat the fractions as integers.

High Performance Arithmetic

For many applications, the speed of arithmetic operations are the bottleneck to performance. Most supercomputers, such as the Cray, the Tera, and the Intel Hypercube are considered “super” because they excel at performing fixed and floating point arithmetic. In this section we discuss a number of ways to improve the speed of addition, subtraction, multiplication, and division.

HIGH PERFORMANCE ADDITION

The ripple-carry adder that we reviewed in Section 3.2.2 may introduce too much delay into a system. The longest path through the adder is from the inputs of the least significant full adder to the outputs of the most significant full adder. The process of summing the inputs at each bit position is relatively fast (a small two-level circuit suffices) but the carry propagation takes a long time to work its way through the circuit. In fact, the propagation time is proportional to the number of bits in the operands. This is unfortunate, since more significant figures in an addition translates to more time to perform the addition. In this section, we look at a method of speeding the carry propagation in what is known as a carry lookahead adder.

In Appendix B, reduced Boolean expressions for the sum (si) and carry outputs (ci+1) of a full adder are created. These expressions are repeated below, with sub- scripts added to denote the relative position of a full adder in a ripple-carry adder:

The Gi and Pi terms are referred to as generate and propagate functions, respectively, for the effect they have on the carry. When Gi = 1, a carry is generated at stage i. When Pi = 1, then a carry is propagated through stage i if either ai or bi is a 1. The Gi and Pi terms can be created in one level of logic since they only depend on an AND or an OR of the input variables, respectively.

We can now create a four-bit carry lookahead adder as shown in Figure 3-17. We still have the delay through the full adders as before, but now the carry chain is broken into independent pieces that require one gate delay for Gi and Pi and two more gate delays to generate ci+1. Thus, a depth of three gate delays is added, but the ripple-carry chain is removed. If we assume that each full adder introduces a gate delay of two, then a four-bit carry lookahead adder will have a maximum gate delay of five, whereas a four-bit ripple-carry adder will have a maximum gate delay of eight. The difference between the two approaches is more pronounced for wider operands. This process is limited to about eight bits of carry-lookahead, because of gate fanin limitations discussed in Appendix A. For additions of numbers having more than eight bits, the carry-lookahead circuits can be cascaded to compute the carry in and carry out of each carry-lookahead unit. (See the EXAMPLE at the end of the chapter.)

HIGH PERFORMANCE MULTIPLICATION

A number of methods exist for speeding the process of multiplication. Two methods are described in the sections below. The first approach gains performance by skipping over blocks of 1’s, which eliminates addition steps. A parallel multiplier is described next, in which a cross product among all pairs of multi- plier and multiplicand bits is formed. The result of the cross product is summed by rows to produce the final product.

The Booth Algorithm

The Booth algorithm treats positive and negative numbers uniformly. It operates on the fact that strings of 0’s or 1’s in the multiplier require no additions – just shifting. Additions or subtractions take place at the boundaries of the strings, where transitions take place from 0 to 1 or from 1 to 0. A string of 1’s in the multiplier from bit positions with weights 2u to 2v can be treated as 2u+1 – 2v. For example, if the multiplier is 001110 (+14)10, then u = 3 and v = 1, so 24 – 21 = 14.

In a hardware implementation, the multiplier is scanned from right to left. The first transition is observed going from 0 to 1, and so 21 is subtracted from the initial value (0). On the next transition, from 1 to 0, 24 is added, which results in +14. A 0 is considered to be appended to the right side of the multiplier in order to define the situation in which a 1 is in the rightmost digit of the multiplier.

If the multiplier is recoded according to the Booth algorithm, then fewer steps may be needed in the multiplication process. Consider the multiplication example shown in Figure 3-18. The multiplier (14)10 contains three 1’s, which means

that three addition operations are required for the shift/add multiplication procedure that is described in Section 3.3.1. The Booth recoded multiplier is obtained by scanning the original multiplier from right to left, and placing a -1 in the position where the first 1 in a string is encountered, and placing a +1 in the position where the next 0 is seen. The multiplier 001110 thus becomes 0 +1 0 0  0. The Booth recoded multiplier contains just two nonzero digits: +1 and -1, which means that only one addition operation and one subtraction operation are needed, and so a savings is realized for this example.

A savings is not always realized, however, and in some cases the Booth algorithm may cause more operations to take place than if it is not used at all. Consider the example shown in Figure 3-19, in which the multiplier consists of alternating 1’s and 0’s. This is the same example shown in Figure 3-18 but with the multiplicand and multiplier swapped. Without Booth recoding of the multiplier, three addition operations are required for the three 1’s in the multiplier. The Booth recoded multiplier, however, requires six addition and subtraction operations, which is clearly worse. We improve on this in the next section.

The Modified Booth Algorithm

One solution to this problem is to group the recoded multiplier bits in pairs, known as bit pair recoding, which is also known as the modified Booth algorithm. Grouping bit pairs from right to left produces three “+1,-1” pairs as shown in Figure 3-20. Since the +1 term is to the left of the -1 term, it has a

weight that is twice as large as the weight for the -1 position. Thus, we might think of the pair as having the collective value +2 – 1 = +1.

In a similar manner, the pair -1,+1 is equivalent to -2 + 1 = -1. The pairs +1,+1 and -1,-1 cannot occur. There are a total of seven pairs that can occur, which are shown in Figure 3-21. For each case, the value of the recoded bit pair is multi-

plied by the multiplicand and is added to the product. In an implementation of bit pair recoding, the Booth recoding and bit pair recoding steps are collapsed into a single step, by observing three multiplier bits at a time, as shown in the corresponding multiplier bit table.

The process of bit pair recoding of a multiplier guarantees that in the worst case, only w/2 additions (or subtractions) will take place for a w-bit multiplier.

Array Multipliers

The serial method we used for multiplying two unsigned integers in Section 3.2.1 requires only a small amount of hardware, but the time required to ultiply two numbers of length w grows as w2. We can speed the multiplication process so that it completes in just 2w steps by implementing the manual process shown in Figure 3-10 in parallel. The general idea is to form a one-bit product between each multiplier bit and each multiplicand bit, and then sum each row of partial product elements from the top to the bottom in systolic (row by row) fashion.

The structure of a systolic array multiplier is shown in Figure 3-22. A partial product (PP) element is shown at the bottom of the figure. A multiplicand bit (mi) and a multiplier bit (qj) are multiplied by the AND gate, which forms a partial product at position (i,j) in the array. This partial product is added with the partial product from the previous stage (bj) and any carry that is generated in the previous stage (aj). The result has a width of 2w, and appears at the bottom of the array (the high order w bits) and at the right of the array (the low order w bits).

3.5.3 HIGH PERFORMANCE DIVISION

We can extend the unsigned integer division technique of Section 3.3.2 to pro- duce a fractional result in computing a/b. The general idea is to scale a and b to look like integers, perform the division process, and then scale the quotient to correspond to the actual result of dividing a by b.

A faster method of division makes use of a lookup table and iteration. An iterative method of finding a root of a polynomial is called Newton’s iteration, which is illustrated in Figure 3-23. The goal is to find where the function f(x) crosses the

The number of bits of precision doubles on each iteration (see [Goldberg, 1990]), and so if we are looking to obtain 32 bits of precision and we start with a single bit of precision, then five iterations are required to reach our target precision. The problem now is to cast division in the form of finding a zero for f(x).

Consider the function 1/x – b which has a zero at 1/b. If we start with b, then we can compute 1/b by iteratively applying Newton’s method. Since f ’(x) = -1/x2, we now have:

Thus, we only need to perform multiplication and subtraction in order to per- form division. Further, if our initial guess for x0 is good enough, then we may only need to perform the iteration a few times.

Before using this method on an example, we need to consider how we will obtain our initial guess. If we are working with normalized fractions, then it is relatively easy to make use of a lookup table for the first few digits. Consider computing 1/.101101 using a 16-bit normalized base 2 fraction in which the leading 1 is not hidden. The first three bits for any binary fraction will be one of the patterns:

.100, .101, .110, or .111. These fractions correspond to the base 10 numbers 1/2, 5/8, 3/4, and 7/8, respectively. The reciprocals of these numbers are 2, 8/5, 4/3, and 8/7, respectively. We can store the binary equivalents in a lookup table, and then retrieve x0 based on the first three bits of b.

The leading 1 in the fraction does not contribute to the precision, and so the leading three bits of the fraction only provide two bits of precision. Thus, the lookup table only needs two bits for each entry, as shown in Figure 3-24.

Now consider computing 1/.1011011 using this floating point representation. We start by finding x0 using the table shown in Figure 3-24. The first three bits of the fraction b are 101, which corresponds to x0 = 01. We compute x1 = x0(2 – x0b) and obtain, in unsigned base 2 arithmetic: x1 = 01(10 – (01)(.1011011)) = 1.0100101. Our two bits of precision have now become four bits of precision.

For this example, we will retain as much intermediate precision as we can. In general, we only need to retain at most 2p bits of intermediate precision for a p-bit result. We iterate again, obtaining eight bits of precision:

3.5.4 RESIDUE ARITHMETIC

Addition, subtraction, and multiplication can all be performed in a single, carry- less step using residue arithmetic. The residue number system is based on relatively prime integers called moduli. The residue of an integer with respect to a particular modulus is the least positive integer remainder of the division of the integer by the modulus. A set of possible moduli are 5, 7, 9, and 4. With these moduli, 5 ´ 7 ´ 9 ´ 4 = 1260 integers can be uniquely represented. A table showing the representation of the first twenty decimal integers using moduli 5, 7, 9, and 4 is shown in Figure 3-25.

Addition and multiplication in the residue number system result in valid residue numbers, provided the size of the chosen number space is large enough to contain the results. Subtraction requires each residue digit of the subtrahend to be complemented with respect to its modulus before performing addition. Addition and multiplication examples are shown in Figure 3-26. For these examples, the

moduli used are 5, 7, 9, and 4. Addition is performed in parallel for each column, with no carry propagation. Multiplication is also performed in parallel for each column, independent of the other columns.

Although residue arithmetic operations can be very fast, there are a number of disadvantages to the system. Division and sign detection are difficult, and a representation for fractions is also difficult. Conversions between the residue number system and weighted number systems are complex, and often require involved methods such as the Chinese remainder theorem. The conversion problem is important because the residue number system is not very useful with- out being translated to a weighted number system so that magnitude comparisons can be made. However, for integer applications in which the time spent in addition, subtraction, and multiplication outweighs the time spent in division, conversion, etc., the residue number system may be a practical approach. An important application area is matrix-vector multiplication, which is used extensively in signal processing.

EXAMPLE: WIDE WORD HIGH PERFORMANCE ADDER

A practical word width for a carry lookahead adder (CLA) is four bits, whereas a 16-bit word width is not as practical because of the large fan-ins and fan-outs of the internal logic. We can subdivide a 16-bit addition problem into four 4-bit groups in which carry lookahead is used within the groups, and in which carry lookahead is also used among the groups. This organization is referred to as a group carry lookahead adder (GCLA). For this example, we will compare a

some additional logic that generates the carries between the four-bit groups. Each group behaves as an ordinary CLA, except that the least significant carry into each CLA is treated as a variable instead of as a 0, and that group generate (GG) and group propagate (GP) signals are generated. A GG signal is generated when a carry is generated somewhere within a group, and all of the more significant propagate signals are true. This means that a carry into a group will propagate all the way through the group. The corresponding equations for the least significant GG and GP signals in Figure 3-27 are shown below:

The carry into each group, except for the carry into CLA₀, is computed from the GG and GP signals. For example, c4 is true when GG₀ is true or when GP₀ and c0 are both true. The corresponding equation is:

Higher order carries out of each group are computed in a similar manner:

In terms of gate delays, a 16-bit CLA has a longest path of five gate delays to pro- duce the most significant sum bit, as discussed in Section 3.5.1. Each of the CLAs in the 16-bit GCLA also has at least five gate delays on the longest path. The GG and GP signals are generated in three gate delays, and the carry signals out of each group are generated in two more gate delays, resulting in a total of five gate delays to generate the carry out of each group. In the highest bit position (s15), five gate delays are needed to generate c12, and another five gate delays are needed to generate s15, for a worst case path of 10 gate delays through the 16-bit GCLA.

With regard to fan-in and fan-out, the maximum fan-in of any gate in a four-bit CLA is four (refer to Figure 3-17), and in general, the maximum fan-in of any gate in an n-bit CLA is n. Thus, the maximum fan-in of any gate in a 16-bit CLA is 16. In comparison, the maximum fan-in for a 16-bit GCLA is five (for generating c16). The fan-outs for both cases are the same as the fan-ins.

In summary, the 16-bit CLA has only half of the depth of the 16-bit GCLA (five gate delays vs. 10 gate delays). The highest fan-in for a 16-bit CLA is 16, which is more than three times the highest fan-in for a 16-bit GCLA (16 vs. five). The highest fan-outs are the same as the highest fan-ins for each case.

3.1 Floating Point Arithmetic

Arithmetic operations on floating point numbers can be carried out using the fixed point arithmetic operations described in the previous sections, with attention given to maintaining aspects of the floating point representation. In the sections that follow, we explore floating point arithmetic in base 2 and base 10, keeping the requirements of the floating point representation in mind.

3.1.1 FLOATING POINT ADDITION AND SUBTRACTION

Floating point arithmetic differs from integer arithmetic in that exponents must be handled as well as the magnitudes of the operands. As in ordinary base 10 arithmetic using scientific notation, the exponents of the operands must be made equal for addition and subtraction. The fractions are then added or subtracted as appropriate, and the result is normalized.

This process of adjusting the fractional part, and also rounding the result can lead to a loss of precision in the result. Consider the unsigned floating point addition (.101 x 2³ + .111 ´ 24) in which the fractions have three significant dig- its. We start by adjusting the smaller exponent to be equal to the larger exponent, and adjusting the fraction accordingly. Thus we have .101 x 2³ = .010 x 2⁴, losing .001 x 2³ of precision in the process. The resulting sum is

and rounding to three significant digits, .100 x 2⁵, and we have lost another 0.001 x 2⁴ in the rounding process.

Why do floating point numbers have such complicated formats?

We may wonder why floating point numbers have such a complicated structure, with the mantissa being stored in signed magnitude representation, the exponent stored in excess notation, and the sign bit separated from the rest of the magnitude by the intervening exponent field. There is a simple explanation for this structure. Consider the complexity of performing floating point arithmetic in a computer. Before any arithmetic can be done, the number must be unpacked from the form it takes in storage. (See Chapter 2 for a description of the IEEE 754 floating point format.) The exponent and mantissa must be extracted from the packed bit pattern before an arithmetic operation can be performed; after the arithmetic operation(s) are performed, the result must be renormalized and rounded, and then the bit patterns are re-packed into the requisite format.

The virtue of a floating point format that contains a sign bit followed by an exponent in excess notation, followed by the magnitude of the mantissa, is that two floating point numbers can be compared for >, <, and = without unpacking. The sign bit is most important in such a comparison, and it appropriately is the MSB in the floating point format. Next most important in comparing two numbers is the exponent, since a change of ± 1 in the exponent changes the value by a factor of 2 (for a base 2 format), whereas a change in even the MSB of the fractional part will change the value of the floating point number by less than that.

In order to account for the sign bit, the signed magnitude fractions are represented as integers and are converted into two’s complement form. After the addition or subtraction operation takes place in two’s complement, there may be a need to normalize the result and adjust the sign bit. The result is then converted back to signed magnitude form.

3.4.2 FLOATING POINT MULTIPLICATION AND DIVISION

Floating point multiplication and division are performed in a manner similar to floating point addition and subtraction, except that the sign, exponent, and fraction of the result can be computed separately. If the operands have the same sign, then the sign of the result is positive. Unlike signs produce a negative result. The exponent of the result before normalization is obtained by adding the exponents of the source operands for multiplication, or by subtracting the divisor exponent from the dividend exponent for division. The fractions are multiplied or divided according to the operation, followed by normalization.

Consider using three-bit fractions in performing the base 2 computation: (+.101 x 22) x (-.110 x 2^-3). The source operand signs differ, which means that the result will have a negative sign. We add exponents for multiplication, and so the exponent of the result is 2 + -3 = -1. We multiply the fractions, which produces the product .01111. Normalizing the product and retaining only three bits in the fraction produces -.111 ´ 2-2.

Now consider using three-bit fractions in performing the base 2 computation:

(+.110 x 2⁵) / (+.100 x 2⁴). The source operand signs are the same, which means that the result will have a positive sign. We subtract exponents for division, and so the exponent of the result is 5 – 4 = 1. We divide fractions, which can be done in a number of ways. If we treat the fractions as unsigned integers, then we will have 110/100 = 1 with a remainder of 10. What we really want is a contiguous set of bits representing the fraction instead of a separate result and remainder, and so we can scale the dividend to the left by two positions, producing the result: 11000/100 = 110. We then scale the result to the right by two positions to restore the original scale factor, producing 1.1. Putting it all together, the result of dividing (+.110 x 2⁵) by (+.100 x 2⁴) produces (+1.10 x 2¹). After normalization, the final result is (+.110 x 2²).

3.1 Fixed Point Multiplication and Division

Multiplication and division of fixed point numbers can be accomplished with addition, subtraction, and shift operations. The sections that follow describe methods for performing multiplication and division of fixed point numbers in both unsigned and signed forms using these basic operations. We will first cover unsigned multiplication and division, and then we will cover signed multiplication and division.

3.1.1 UNSIGNED MULTIPLICATION

Multiplication of unsigned binary integers is handled similar to the way it is carried out by hand for decimal numbers. Figure 3-10 illustrates the multiplication process for two unsigned binary integers. Each bit of the multiplier determines whether or not the multiplicand, shifted left according to the position of the multiplier bit, is added into the product. When two unsigned n-bit numbers are multiplied, the result can be as large as 2n bits. For the example shown in Figure 3-10, the multiplication of two four-bit operands results in an eight-bit product. When two signed n-bit numbers are multiplied, the result can be as large as only

A hardware implementation of integer multiplication can take a similar form to the manual method. Figure 3-11 shows a layout of a multiplication unit for

four-bit numbers, in which there is a four-bit adder, a control unit, three four-bit registers, and a one-bit carry register. In order to multiply two numbers, the multiplicand is placed in the M register, the multiplier is placed in the Q register, and the A and C registers are cleared to zero. During multiplication, the rightmost bit of the multiplier determines whether the multiplicand is added into the product at each step. After the multiplicand is added into the product, the multiplier and the A register are simultaneously shifted to the right. This has the effect of shifting the multiplicand to the left (as for the manual process) and exposing the next bit of the multiplier in position q0.

Figure 3-12 illustrates the multiplication process. Initially, C and A are cleared,.

and M and Q hold the multiplicand and multiplier, respectively. The rightmost bit of Q is 1, and so the multiplier M is added into the product in the A register. The A and Q registers together make up the eight-bit product, but the A register is where the multiplicand is added. After M is added to A, the A and Q registers are shifted to the right. Since the A and Q registers are linked as a pair to form the eight-bit product, the rightmost bit of A is shifted into the leftmost bit of Q. The rightmost bit of Q is then dropped, C is shifted into the leftmost bit of A, and a 0 is shifted into C.

The process continues for as many steps as there are bits in the multiplier. On the second iteration, the rightmost bit of Q is again 1, and so the multiplicand is added to A and the C/A/Q combination is shifted to the right. On the third iteration, the rightmost bit of Q is 0 so M is not added to A, but the C/A/Q combination is still shifted to the right. Finally, on the fourth iteration, the rightmost bit of Q is again 1, and so M is added to A and the C/A/Q combination is shifted to the right. The product is now contained in the A and Q registers, in which A holds the high-order bits and Q holds the low-order bits.

3.1.2 UNSIGNED DIVISION

In longhand binary division, we must successively attempt to subtract the divisor from the dividend, using the fewest number of bits in the dividend as we can. Figure 3-13 illustrates this point by showing that (11)2 does not “fit” in 0 or 01,

but does fit in 011 as indicated by the pattern 001 that starts the quotient.

Computer-based division of binary integers can be handled similar to the way that binary integer multiplication is carried out, but with the complication that the only way to tell if the dividend does not “fit” is to actually do the subtraction and test if the remainder is negative. If the remainder is negative then the sub- traction must be “backed out” by adding the divisor back in, as described below.

In the division algorithm, instead of shifting the product to the right as we did for multiplication, we now shift the quotient to the left, and we subtract instead of adding. When two n-bit unsigned numbers are being divided, the result is no larger than n bits.

Figure 3-14 shows a layout of a division unit for four-bit numbers in which there

is a five-bit adder, a control unit, a four-bit register for the dividend Q, and two five-bit registers for the divisor M and the remainder A. Five-bit registers are used for A and M, instead of 4-bit registers as we might expect, because an extra bit is needed to indicate the sign of the intermediate result. Although this division method is for unsigned numbers, subtraction is used in the process and negative partial results sometimes arise, which extends the range from -16 through +15, thus there is a need for 5 bits to store intermediate results.

In order to divide two four-bit numbers, the dividend is placed in the Q register, the divisor is placed in the M register, and the A register and the high order bit of M are cleared to zero. The leftmost bit of the A register determines whether the divisor is added back into the dividend at each step. This is necessary in order to restore the dividend when the result of subtracting the divisor is negative, as described above. This is referred to as restoring division, because the dividend is restored to its former value when the remainder is negative. When the result is not negative, then the least significant bit of Q is set to 1, which indicates that the divisor “fits” in the dividend at that point.

Figure 3-15 illustrates the division process. Initially, A and the high order bit of M are cleared, and Q and the low order bits of M are loaded with the dividend and divisor, respectively. The A and Q registers are shifted to the left as a pair and the divisor M is subtracted from A. Since the result is negative, the divisor is added back to restore the dividend, and q0 is cleared to 0. The process repeats by shifting A and Q to the left, and by subtracting M from A. Again, the result is negative, so the dividend is restored and q0 is cleared to 0. On the third iteration, A and Q are shifted to the left and M is again subtracted from A, but now the result of the subtraction is not negative, so q0 is set to 1. The process continues for one final iteration, in which A and Q are shifted to the left and M is subtracted from A, which produces a negative result. The dividend is restored and q0 is cleared to 0. The quotient is now contained in the Q register and the remain- der is contained in the A register.

3.1.3 SIGNED MULTIPLICATION AND DIVISION

If we apply the multiplication and division methods described in the previous sections to signed integers, then we will run into some trouble. Consider multi- plying -1 by +1 using four-bit words, as shown in the left side of Figure 3-16. The eight-bit equivalent of +15 is produced instead of -1. What went wrong is that the sign bit did not get extended to the left of the result. This is not a problem for a positive result because the high order bits default to 0, producing the correct sign bit 0.

A solution is shown in the right side of Figure 3-16, in which each partial product is extended to the width of the result, and only the rightmost eight bits of the result are retained. If both operands are negative, then the signs are extended for both operands, again retaining only the rightmost eight bits of the result.

Signed division is more difficult. We will not explore the methods here, but as a general technique, we can convert the operands into their positive forms, per- form the division, and then convert the result into its true signed form as a final step.

ARITHMETIC

Overview

In the previous chapter we explored a few ways that numbers can be represented in a digital computer, but we only briefly touched upon arithmetic operations that can be performed on those numbers. In this chapter we cover four basic arithmetic operations: addition, subtraction, multiplication, and division. We begin by describing how these four operations can be performed on fixed point numbers, and continue with a description of how these four operations can be performed on floating point numbers.

Some of the largest problems, such as weather calculations, quantum mechanical simulations, and land-use modeling, tax the abilities of even today’s largest computers. Thus the topic of high-performance arithmetic is also important. We conclude the chapter with an introduction to some of the algorithms and techniques used in speeding arithmetic operations.

Fixed Point Addition and Subtraction

The addition of binary numbers and the concept of overflow were briefly dis- cussed in Chapter 2. Here, we cover addition and subtraction of both signed and unsigned fixed point numbers in detail. Since the two’s complement representation of integers is almost universal in today’s computers, we will focus primarily on two’s complement operations. We will briefly cover operations on 1’s complement and BCD numbers, which have a foundational significance for other areas of computing, such as networking (for 1’s complement addition) and hand-held calculators (for BCD arithmetic.)

TWO’S COMPLEMENT ADDITION AND SUBTRACTION

In this section, we look at the addition of signed two’s complement numbers. As we explore the addition of signed numbers, we also implicitly cover subtraction as well, as a result of the arithmetic principle:

a – b = a + (-b).

We can negate a number by complementing it (and adding 1, for two’s complement), and so we can perform subtraction by complementing and adding. This results in a savings of hardware because it avoids the need for a hardware subtractor. We will cover this topic in more detail later.

We will need to modify the interpretation that we place on the results of addition when we add two’s complement numbers. To see why this is the case, consider Figure 3-1. With addition on the real number line, numbers can be as large or as

small as desired—the number line goes to ±¥, so the real number line can accommodate numbers of any size. On the other hand, as discussed in Chapter 2, computers represent data using a finite number of bits, and as a result can only store numbers within a certain range. For example, an examination of Table 2.1 shows that if we restrict the size of a number to, for example, 3 bits, there will only be eight possible two’s complement values that the number can assume. In Figure 3-1 these values are arranged in a circle beginning with 000 and proceeding around the circle to 111 and then back to 000. The figure also shows the decimal equivalents of these same numbers.

Some experimentation with the number circle shows that numbers can be added or subtracted by traversing the number circle clockwise for addition and counterclockwise for subtraction. Numbers can also be subtracted by two’s complementing the subtrahend and adding. Notice that overflow can only occur for addition when the operands (“addend” and “augend”) are of the same sign. Furthermore, overflow occurs if a transition is made from +3 to -4 while proceeding around the number circle when adding, or from -4 to +3 while subtracting. (Two’s complement overflow is discussed in more detail later in the chapter.)

Here are two examples of 8-bit two’s complement addition, first using two positive numbers:

The carry produced by addition at the highest (leftmost) bit position is discarded in two’s complement addition. A similar situation arises with a carry out of the highest bit position when adding two negative numbers:

The carry out of the leftmost bit is discarded because the number system is modular—it “wraps around” from the largest positive number to the largest negative number as Figure 3-1 shows.

Although an addition operation may have a (discarded) carry-out from the MSB, this does not mean that the result is erroneous. The two examples above yield correct results in spite of the fact that there is a carry-out of the MSB. The next section discusses overflow in two’s complement addition in more detail.

Overflow

When two numbers are added that have large magnitudes and the same sign, an overflow will occur if the result is too large to fit in the number of bits used in the representation. Consider adding (+80)10 and (+50)10 using an eight bit for- mat. The result should be (+130)10, however, as shown below, the result is (-126)10:

This should come as no surprise, since we know that the largest positive 8-bit two’s complement number is +(127)₁₀, and it is therefore impossible to represent (+130)10. Although the result 10000010₂ “looks” like 13010 if we think of it in unsigned form, the sign bit indicates a negative number in the signed form, which is clearly wrong.

In general, if two numbers of opposite signs are added, then an overflow cannot occur. Intuitively, this is because the magnitude of the result can be no larger than the magnitude of the larger operand. This leads us to the definition of two’s complement overflow:

If the numbers being added are of the same sign and the result is of the opposite sign, then an overflow occurs and the result is incorrect. If the numbers being added are of opposite signs, then an overflow will never occur. As an alternative method of detecting overflow for addition, an overflow occurs if and only if the carry into the sign bit differs from the carry out of the sign bit.

If a positive number is subtracted from a negative number and the result is positive, or if a negative number is subtracted from a positive number and the result is negative, then an overflow occurs. If the numbers being subtracted are of the same sign, then an overflow will never occur.

HARDWARE IMPLEMENTATION OF ADDERS AND SUBTRACTORS

Up until now we have focused on algorithms for addition and subtraction. Now we will take a look at implementations of simple adders and subtractors.

Ripple-Carry Addition and Ripple-Borrow Subtraction

In Appendix A, a design of a four-bit ripple-carry adder is explored. The adder is modeled after the way that we normally perform decimal addition by hand, by summing digits in one column at a time while moving from right to left. In this section, we review the ripple-carry adder, and then take a look at a ripple-borrow subtractor. We then combine the two into a single addition/subtraction unit.

Figure 3-2 shows a 4-bit ripple-carry adder that is developed in Appendix A. Two

binary numbers A and B are added from right to left, creating a sum and a carry at the outputs of each full adder for each bit position.

Four 4-bit ripple-carry adders are cascaded in Figure 3-3 to add two 16-bit numbers. The rightmost full adder has a carry-in of 0. Although the rightmost full adder can be simplified as a result of the carry-in of 0, we will use the more general form and force c0 to 0 in order to simplify subtraction later on.

Subtraction of binary numbers proceeds in a fashion analogous to addition. We can subtract one number from another by working in a single column at a time, subtracting digits of the subtrahend bi, from the minuend ai, as we move from right to left. As in decimal subtraction, if the subtrahend is larger than the minuend or there is a borrow from a previous digit then a borrow must be propagated

trates a four-bit ripple-borrow subtractor that is made up of four full subtractors.

As discussed above, an alternative method of implementing subtraction is to form the two’s complement negative of the subtrahend and add it to the minuend. The circuit that is shown in Figure 3-6 performs both addition and subtrac-

tion on four-bit two’s complement numbers by allowing the bi inputs to be complemented when subtraction is desired. An ADD /SUBTRACT control line determines which function is performed. The bar over the ADD symbol indicates the ADD operation is active when the signal is low. That is, if the control line is 0, then the ai and bi inputs are passed through to the adder, and the sum is generated at the si outputs. If the control line is 1, then the ai inputs are passed through to the adder, but the bi inputs are one’s complemented by the XOR gates before they are passed on to the adder. In order to form the two’s complement negative, we must add 1 to the one’s complement negative, which is accomplished by setting the carry_in line (c0) to 1 with the control input. In this way, we can share the adder hardware among both the adder and the subtractor.

ONE’S COMPLEMENT ADDITION AND SUBTRACTION

Although it is not heavily used in mainstream computing anymore, the one’s complement representation was used in early computers. One’s complement addition is handled somewhat differently from two’s complement addition: the carry out of the leftmost position is not discarded, but is added back into the least significant position of the integer portion as shown in Figure 3-7. This is

number circle has two positions for 0. When we add two numbers, if we traverse through both -0 and +0, then we must compensate for the fact that 0 is visited twice. The end-around carry advances the result by one position for this situation.

Notice that the distance between -0 and +0 on the number circle is the distance between two integers, and is not the distance between two successive represent- able numbers. As an illustration of this point, consider adding (5.5)10 and

(-1.0)10 in one’s complement arithmetic, which is shown in Figure 3-9. (Note that we can also treat this as a subtraction problem, in which the subtrahend is negated by complementing all of the bits, before adding it to the minuend.) In

order to add (+5.5)10 and (-1.0)10 and obtain the correct result in one’s complement, we add the end-around carry into the one’s position as shown. This adds complexity to our number circle, because in the gap between +0 and -0, there are valid numbers that represent fractions that are less than 0, yet they appear on the number circle before -0 appears. If the number circle is reordered to avoid this anomaly, then addition must be handled in a more complex manner.

The need to look for two different representations for zero, and the potential need to perform another addition for the end-around carry are two important reasons for preferring the two’s complement arithmetic to one’s complement arithmetic.

■ SUMMARY

All data in a computer is represented in terms of bits, which can be organized and interpreted as integers, fixed point numbers, floating point numbers, or characters.

Character codes, such as ASCII, EBCDIC, and Unicode, have finite sizes and can thus be completely represented in a finite number of bits. The number of bits used for representing numbers is also finite, and as a result only a subset of the real numbers can be represented. This leads to the notions of range, precision, and error. The range for a number representation defines the largest and smallest magnitudes that can be represented, and is almost entirely determined by the base and the number of bits in the exponent for a floating point representation. The precision is determined by the number of bits used in representing the magnitude (excluding the exponent bits in a floating point representation). Error arises in floating point representations because there are real numbers that fall within the gaps between adjacent representable numbers.

■ Further Reading

(Hamacher et al., 1990) provides a good explanation of biased error in floating point representations. The IEEE 754 floating point standard is described in (IEEE, 1985). The analysis of range, error, and precision in Section 2.3 was influenced by (Forsythe, 1970). The GAO report (U.S. GAO report GAO/IMTEC-92-26) gives a very readable account of the software problem that led to the Patriot failure in Dhahran. See http://www.unicode.org for information on the Unicode standard.

■ PROBLEMS

2.1 Given a signed, fixed point representation in base 10, with three digits to the left and right of the decimal point:

a) What is the range? (Calculate the highest positive number and the lowest negative number.)

b) What is the precision? (Calculate the difference between two adjacent numbers on a number line. Remember that the error is 1/2 the precision.)

2.2 Convert the following numbers as indicated, using as few digits in the results as necessary.

a) (47)₁₀ to unsigned binary.

b) (-27)₁₀ to binary signed magnitude.

c) (213)₁₆ to base 10.

d) (10110.101)₂ to base 10.

e) (34.625)₁₀ to base 4.

2.3 Convert the following numbers as indicated, using as few digits in the results as necessary.

a) (011011)₂ to base 10.

b) (-27)₁₀ to excess 32 in binary. c) (011011)2 to base 16.

d) (55.875)₁₀ to unsigned binary. e) (132.2)4 to base 16.

2.4 Convert .2013 to decimal.

2.5 Convert (43.3)7 to base 8 using no more than one octal digit to the right of the radix point. Truncate any remainder by chopping excess digits. Use an ordinary unsigned octal representation.

2.6 Represent (17.5)10 in base 3, then convert the result back to base 10. Use two digits of precision to the right of the radix point for the intermediate base 3 form.

2.7 Find the decimal equivalent of the four-bit two’s complement number: 1000.

2.8 Find the decimal equivalent of the four-bit one’s complement number: 1111.

2.9 Show the representation for (305)10 using three BCD digits.

2.10 Show the 10’s complement representation for (-305)10 using three BCD digits.

2.11 For a given number of bits, are there more representable integers in one’s

complement, two’s complement, or are they the same?

2.12 Complete the following table for the 5-bit representations (including the sign bits) indicated below. Show your answers as signed base 10 integers.

2.13 Complete the following table using base 2 scientific notation and an eight-bit floating point representation in which there is a three-bit exponent in excess 3 notation (not excess 4), and a four-bit normalized fraction with a hidden ‘1’. In this representation, the hidden 1 is to the left of the radix point. This means that the number 1.0101 is in normalized form, whereas .101 is not.

2.14 The IBM short floating point representation uses base 16, one sign bit, a seven-bit excess 64 exponent and a normalized 24-bit fraction.

a) What number is represented by the bit pattern shown below? 1 0111111 01110000 00000000 00000000 Show your answer in decimal. Note: the spaces are included in the number for readability only.

b) Represent (14.3)6 in this notation.

2.15 For a normalized floating point representation, keeping everything else the same but:

a) decreasing the base will increase / decrease / not change the number of representable numbers.

b) increasing the number of significant digits will increase / decrease / not change the smallest representable positive number.

c) increasing the number of bits in the exponent will increase / decrease / not change the range.

d) changing the representation of the exponent from excess 64 to two’s complement will increase / decrease / not change the range.

2.16 For parts (a) through (e), use a floating point representation with a sign bit in the leftmost position, followed by a two-bit two’s complement exponent, followed by a normalized three-bit fraction in base 2. Zero is represented by the bit pattern: 0 0 0 0 0 0. There is no hidden ‘1’.

a) What decimal number is represented by the bit pattern: 1 0 0 1 0 0?

b) Keeping everything else the same but changing the base to 4 will: increase / decrease / not change the smallest representable positive number.

c) What is the smallest gap between successive numbers?

d) What is the largest gap between successive numbers?

e) There are a total of six bits in this floating point representation, and there are 26 = 64 unique bit patterns. How many of these bit patterns are valid?

2.17 Represent (107.15)10 in a floating point representation with a sign bit, a seven-bit excess 64 exponent, and a normalized 24-bit fraction in base 2. There is no hidden 1. Truncate the fraction by chopping bits as necessary.

2.18 For the following single precision IEEE 754 bit patterns show the numer- ical value as a base 2 significand with an exponent (e.g. 1.11 ´ 25).

a) 0 10000011 01100000000000000000000

b) 1 10000000 00000000000000000000000

c) 1 00000000 00000000000000000000000

d) 1 11111111 00000000000000000000000

e) 0 11111111 11010000000000000000000

f ) 0 00000001 10010000000000000000000

g) 0 00000011 01101000000000000000000

2.19 Show the IEEE 754 bit patterns for the following numbers:

a) +1.1011 x 25 (single precision)

b) +0 (single precision)

c) -1.00111 x 2-1 (double precision)

d) -NaN (single precision)

2.20 Using the IEEE 754 single precision format, show the value (not the bit pattern) of:

a) The largest positive representable number (note: ¥ is not a number).

b) The smallest positive nonzero number that is normalized.

c) The smallest positive nonzero number in denormalized format.

d) The smallest normalized gap.

e) The largest normalized gap.

f) ) The number of normalized representable numbers (including 0; note that and NaN are not numbers).

2.21 Two programmers write random number generators for normalized floating point numbers using the same method. Programmer A’s generator creates random numbers on the closed interval from 0 to 1/2, and programmer B’s generator creates random numbers on the closed interval from 1/2 to 1. Programmer B’s generator works correctly, but Programmer A’s generator produces a skewed distribution of numbers. What could be the problem with Programmer A’s approach?

2.22 A hidden 1 representation will not work for base 16. Why not?

2.23 With a hidden 1 representation, can 0 be represented if all possible bit patterns in the exponent and fraction fields are used for nonzero numbers?

2.24 Given a base 10 floating point number (e.g. .583 x 10³), can the number be converted into the equivalent base 2 form: .x X 2y by separately converting the fraction (.583) and the exponent (3) into base 2?

2.3 Case Study: Patriot Missile Defense Failure Caused by Loss of Precision

During the 1991-1992 Operation Desert Storm conflict between Coalition forces and Iraq, the Coalition used a military base in Dhahran, Saudi Arabia that was protected by six U.S. Patriot Missile batteries. The Patriot system was originally designed to be mobile and to operate for only a few hours in order to avoid detection.

The Patriot system tracks and intercepts certain types of objects, such as cruise missiles or Scud ballistic missiles, one of which hit a U.S. Army barracks at Dhahran on February 5, 1991, killing 28 Americans. The Patriot system failed to track and intercept the incoming Scud due to a loss of precision in converting integers to a floating point number representation.

A radar system operates by sending out a train of electromagnetic pulses in various directions and then listening for return signals that are reflected from objects in the path of the radar beam. If an airborne object of interest such as a Scud is detected by the Patriot radar system, then the position of a range gate is deter- mined (see Figure 2-12), which estimates the position of the object being tracked

during the next scan. The range gate also allows information outside of its boundaries to be filtered out, which simplifies tracking. The position of the object (a Scud for this case) is confirmed if it is found within the range gate.

The prediction of where the Scud will next appear is a function of the Scud’s velocity. The Scud’s velocity is determined by its change in position with respect to time, and time is updated in the Patriot’s internal clock in 100 ms intervals. Velocity is represented as a 24-bit floating point number, and time is represented as a 24-bit integer, but both must be represented as 24-bit floating point numbers in order to predict where the Scud will next appear.

The conversion from integer time to real time results in a loss of precision that increases as the internal clock time increases. The error introduced by the conversion results in an error in the range gate calculation, which is proportional to the target’s velocity and the length of time that the system is running. The cause of the Dhahran incident, after the Patriot battery had been operating continuously for over 100 hours, is that the range gate shifted by 687 m, resulting in the failed interception of a Scud.

The conversion problem was known two weeks in advance of the Dhahran incident as a result of data provided by Israel, but it took until the day after the attack for new software to arrive due to the difficulty of distributing bug fixes in a wartime environment. A solution to the problem, until a software fix could be made available, would have been to simply reboot the system every few hours which would have the effect of resetting the internal clock. Since field personnel were not informed of how long was too long to keep a system running, which was in fact known at the time from data provided by Israel, this solution was never implemented. The lesson for us is to be very aware of the limitations of relying on calculations that use finite precision.

2.4 Character Codes

Unlike real numbers, which have an infinite range, there is only a finite number of characters. An entire character set can be represented with a small number of bits per character. Three of the most common character representations, ASCII, EBCDIC, and Unicode, are described here.

2.4.1 THE ASCII CHARACTER SET

The American Standard Code for Information Interchange (ASCII) is summarized in Figure 2-13, using hexadecimal indices. The representation for each character consists of 7 bits, and all 27 possible bit patterns represent valid characters. The characters in positions 00 – 1F and position 7F are special control characters that are used for transmission, printing control, and other non-textual purposes. The remaining characters are all printable, and include letters, numbers, punctuation, and a space. The digits 0-9 appear in sequence, as do the upper and lower case letters1. This organization simplifies character manipulation. In order to change the character representation of a digit into its numerical value, we can subtract (30)₁₆ from it. In order to convert the ASCII character ‘5,’ which is in position (35)₁₆, into the number 5, we compute (35 – 30 = 5)₁₆. In

order to convert an upper case letter into a lower case letter, we add (20)₁₆. For example, to convert the letter ‘H,’ which is at location (48)16 in the ASCII table, into the letter ‘h,’ which is at position (68)₁₆, we compute (48 + 20 = 68)₁₆.

2.4.2 THE EBCDIC CHARACTER SET

A problem with the ASCII code is that only 128 characters can be represented, which is a limitation for many keyboards that have a lot of special characters in addition to upper and lower case letters. The Extended Binary Coded Decimal Interchange Code (EBCDIC) is an eight-bit code that is used extensively in IBM mainframe computers. Since seven-bit ASCII characters are frequently represented in an eight-bit modified form (one character per byte), in which a 0 or a 1 is appended to the left of the seven-bit pattern, the use of EBCDIC does not place a greater demand on the storage of characters in a computer. For serial transmission, however, (see Chapter 8), an eight-bit code takes more time to transmit than a seven-bit code, and for this case the wider code does make a difference.

The EBCDIC code is summarized in Figure 2-14. There are gaps in the table, which can be used for application specific characters. The fact that there are gaps in the upper and lower case sequences is not a major disadvantage because character manipulations can still be done as for ASCII, but using different offsets.

2.4.3 THE UNICODE CHARACTER SET

The ASCII and EBCDIC codes support the historically dominant (Latin) character sets used in computers. There are many more character sets in the world, and a simple ASCII-to-language-X mapping does not work for the general case, and so a new universal character standard was developed that supports a great breadth of the world’s character sets, called Unicode.

Unicode is an evolving standard. It changes as new character sets are introduced into it, and as existing character sets evolve and their representations are refined. In version 2.0 of the Unicode standard, there are 38,885 distinct coded characters that cover the principal written languages of the Americas, Europe, the Middle East, Africa, India, Asia, and Pacifica.

The Unicode Standard uses a 16-bit code set in which there is a one-to-one correspondence between 16-bit codes and characters. Like ASCII, there are no complex modes or escape codes. While Unicode supports many more characters than ASCII or EBCDIC, it is not the end-all standard. In fact, the 16-bit Unicode standard is a subset of the 32-bit ISO 10646 Universal Character Set (UCS-4).

Glyphs for the first 256 Unicode characters are shown in Figure 2-15, according to Unicode version 2.1. Note that the first 128 characters are the same as for ASCII.

2.3 Floating Point N umbers

The fixed point number representation, which we explored in Section 2.2, has a fixed position for the radix point, and a fixed number of digits to the left and right of the radix point. A fixed point representation may need a great many dig- its in order to represent a practical range of numbers. For example, a computer that can represent a number as large as a trillion1 maintains at least 40 bits to the left of the radix point since 240 » 1012. If the same computer needs to represent one trillionth, then 40 bits must also be maintained to the right of the radix point, which results in a total of 80 bits per number.

In practice, much larger numbers and much smaller numbers appear during the course of computation, which places even greater demands on a computer. A great deal of hardware is required in order to store and manipulate numbers with 80 or more bits of precision, and computation proceeds more slowly for a large number of digits than for a small number of digits. Fine precision, however, is generally not needed when large numbers are used, and conversely, large numbers do not generally need to be represented when calculations are made with small numbers. A more efficient computer can be realized when only as much precision is retained as is needed.

2.3.1 RANGE AND PRECISION IN FLOATING POINT NUMBERS

A floating point representation allows a large range of expressible numbers to be represented in a small number of digits by separating the digits used for precision from the digits used for range. The base 10 floating point number representing Avogadro’s number is shown below:

1. In the American number system, which is used here, a trillion = 1012. In the British number system, this is a “million million,” or simply a “billion.” The British “milliard,” or a “thou- sand million” is what Americans call a “billion.”

Here, the range is represented by a power of 10, 1023 in this case, and the precision is represented by the digits in the fixed point number, 6.023 in this case. In discussing floating point numbers, the fixed point part is often referred to as the mantissa, or significand of the number. Thus a floating point number can be characterized by a triple of numbers: sign, exponent, and significand.

The range is determined primarily by the number of digits in the exponent (two digits are used here) and the base to which it is raised (base 10 is used here) and the precision is determined primarily by the number of digits in the significand (four digits are used here). Thus the entire number can be represented by a sign and 6 digits, two for the exponent and four for the significand. Figure 2-7 shows how the triple of sign, exponent, significand, might be formatted in a computer.

Notice how the digits are packed together with the sign first, followed by the exponent, followed by the significand. This ordering will turn out to be helpful in comparing two floating point numbers. The reader should be aware that the decimal point does not need to be stored with the number as long as the decimal point is always in the same position in the significand. (This will be discussed in Section 2.3.2.)

If we need a greater range, and if we are willing to sacrifice precision, then we can use just three digits in the fraction and have three digits left for the exponent without increasing the number of digits used in the representation. An alternative method of increasing the range is to increase the base, which has the effect of increasing the precision of the smallest numbers but decreasing the precision of the largest numbers. The range/precision trade-off is a major advantage of using a floating point representation, but the reduced precision can cause problems, sometimes leading to disaster, an example of which is described in Section 2.4.

2.3.2 NORMALIZATION, AND THE HIDDEN BIT

A potential problem with representing floating point numbers is that the same number can be represented in different ways, which makes comparisons and arithmetic operations difficult. For example, consider the numerically equivalent forms shown below:

In order to avoid multiple representations for the same number, floating point numbers are maintained in normalized form. That is, the radix point is shifted to the left or to the right and the exponent is adjusted accordingly until the radix point is to the left of the leftmost nonzero digit. So the rightmost number above is the normalized one. Unfortunately, the number zero cannot be represented in this scheme, so to represent zero an exception is made. The exception to this rule is that zero is represented as all 0’s in the mantissa.

If the mantissa is represented as a binary, that is, base 2, number, and if the normalization condition is that there is a leading “1” in the normalized mantissa, then there is no need to store that “1” and in fact, most floating point formats do not store it. Rather, it is “chopped off ” before packing up the number for storage, and it is restored when unpacking the number into exponent and mantissa. This results in having an additional bit of precision on the right of the number, due to removing the bit on the left. This missing bit is referred to as the hidden bit, also known as a hidden 1. For example, if the mantissa in a given format is .11010 after normalization, then the bit pattern that is stored is 1010—the left-most bit is truncated, or hidden. We will see that the IEEE 754 floating point format uses a hidden bit.

2.3.3 REPRESENTING FLOATING POINT NUMBERS IN THE COM- PUTER—PRELIMINARIES

Let us design a simple floating point format to illustrate the important factors in representing floating point numbers on the computer. Our format may at first seem to be unnecessarily complex. We will represent the significand in signed magnitude format, with a single bit for the sign bit, and three hexadecimal digits for the magnitude. The exponent will be a 3-bit excess-4 number, with a radix of 16. The normalized form of the number has the hexadecimal point to the left of the three hexadecimal digits.

The bits will be packed together as follows: The sign bit is on the left, followed by the 3-bit exponent, followed by the three hexadecimal digits of the significand. Neither the radix nor the hexadecimal point will be stored in the packed form.

The reason for these rather odd-seeming choices is that numbers in this format can be compared for in their “packed” format, which is shown in the illustration below:

Consider representing (358)10 in this format.

The first step is to convert the fixed point number from its original base into a fixed point number in the target base. Using the method described in Section 2.1.3, we convert the base 10 number into a base 16 number as shown below:

Thus (358)10 = (166)16. The next step is to convert the fixed point number into a floating point number:

Note that the form 160 reflects a base of 16 with an exponent of 0, and that the number 16 as it appears on the page uses a base 10 form. That is, (160)10 = (100)16. This is simply a notational convenience used in describing a floating point number.

The next step is to normalize the number:

Finally, we fill in the bit fields of the number. The number is positive, and so we place a 0 in the sign bit position. The exponent is 3, but we represent it in excess 4, so the bit pattern for the exponent is computed as shown below:

Alternatively, we could have simply computed 3 + 4 = 7 in base 10, and then made the equivalent conversion (7)₁₀ = (111)₂.

Finally, each of the base 16 digits is represented in binary as 1 = 0001, 6 = 0110, and 6 = 0110. The final bit pattern is shown below:

Notice again that the radix point is not explicitly represented in the bit pattern, but its presence is implied. The spaces between digits are for clarity only, and do not suggest that the bits are stored with spaces between them. The bit pattern as stored in a computer’s memory would look like this:

0111000101100110

The use of an excess 4 exponent instead of a two’s complement or a signed magnitude exponent simplifies addition and subtraction of floating point numbers (which we will cover in detail in Chapter 3). In order to add or subtract two normalized floating point numbers, the smaller exponent (smaller in degree, not magnitude) must first be increased to the larger exponent (this retains the range), which also has the effect of unnormalizing the smaller number. In order to deter- mine which exponent is larger, we only need to treat the bit patterns as unsigned numbers and then make our comparison. That is, using an excess 4 representation, the smallest exponent is -4, which is represented as 000. The largest exponent is +3, which is represented as 111. The remaining bit patterns for -3, -2, -1, 0, +1, and +2 fall in their respective order as 001, 010, 011, 100, 101, and 110.

Now if we are given the bit pattern shown above for (358)10 along with a description of the floating point representation, then we can easily determine the number. The sign bit is a 0, which means that the number is positive. The exponent in unsigned form is the number (+7)10, but since we are using excess 4, we

must subtract 4 from it, which results in an actual exponent of (+7 – 4 = +3)10. The fraction is grouped in four-bit hexadecimal digits, which gives a fraction of (.166)16. Putting it all together results in (+.166 ´ 163)16 = (358)10.

Now suppose that only 10 bits are allowed for the fraction in the above example, instead of the 12 bits that group evenly into fours for hexadecimal digits. How does the representation change? One approach might be to round the fraction and adjust the exponent as necessary. Another approach, which we use here, is to simply truncate the least significant bits by chopping and avoid making adjustments to the exponent, so that the number we actually represent is:

If we treat the missing bits as 0’s, then this bit pattern represents (.164 ´ 163)16. This method of truncation produces a biased error, since values of 00, 01, 10, and 11 in the missing bits are all treated as 0, and so the error is in the range from 0 to (.003)16. The bias comes about because the error is not symmetric about 0. We will not explore the bias problem further here, but a more thorough discussion can be found in (Hamacher et al., 1990).

We again stress that whatever the floating point format is, that it be known to all parties that intend to store or retrieve numbers in that format. The Institute of Electrical and Electronics Engineers (IEEE), has taken the lead in standardizing floating point formats. The IEEE 754 floating point format, which is in nearly universal usage, is discussed in Section 2.3.5.

2.3.4 ERROR IN FLOATING POINT REPRESENTATIONS

The fact that finite precision introduces error means that we should consider how great the error is (by “error”, we mean the distance between two adjacent representable numbers), and whether it is acceptable for our application. As an example of a potential pitfall, consider representing one million in floating point, and then subtracting one million 1’s from it. We may still be left with a million if the error is greater than 1.¹

In order to characterize error, range, and precision, we use the following notation:

The number of significant digits in the fraction is represented by s, which is different than the number of bits in the fraction if the base is anything other than 2 (for example, base 16 uses four bits for each digit). In general, if the base is 2k where k is an integer, then k bits are needed to represent each digit. The use of a hidden 1 increases s by one bit even though it does not increase the number of representable numbers. In the previous example, there are three significant digits in the base 16 fraction and there are 12 bits that make up the three digits. There are three bits in the excess 4 exponent, which gives an exponent range of [-22 to 22 – 1]. For this case, b = 16, s = 3, M = 3, and m = -4.

In the analysis of a floating point representation, there are five characteristics that we consider: the number of representable numbers, the numbers that have the largest and smallest magnitudes (other than zero), and the sizes of the largest and smallest gaps between successive numbers.

The number of representable numbers can be determined as shown in Figure

2-8. The sign bit can take on two values, as indicated by the position marked

with an encircled “A.” The total number of exponents is indicated in position B. Note that not all exponent bit patterns are valid in all representations. The IEEE 754 floating point standard, which we will study shortly, has a smallest exponent of -126 even though the eight-bit exponent can support a number as small as -128. The forbidden exponents are reserved for special numbers, such as zero and infinity.

The first digit of the fraction is considered next, which can take on any value except 0 in a normalized representation (except when a hidden 1 is used) as indicated by (b – 1) at position C. The remaining digits of the fraction can take on any of the b values for the base, as indicated by bs-1 at position D. If a hidden 1 is used, then position C is removed and position 4 is replaced with bs. Finally, there must be a representation for 0, which is accounted for in position E.

Consider now the numbers with the smallest and largest magnitudes. The number with the smallest magnitude has the smallest exponent and the smallest non- zero normalized fraction. There must be a nonzero value in the first digit, and

since a 1 is the smallest value we can place there, the smallest fraction is b-1. The number with the smallest magnitude is then bm·b-1 = bm-1. Similarly, the number with the largest magnitude has the largest exponent and the largest fraction (when the fraction is all 1’s), which is equal to bM ·(1 – b–s).

The smallest and largest gaps are computed in a similar manner. The smallest gap occurs when the exponent is at its smallest value and the least significant bit of the fraction changes. This gap is bm·b–s = bm–s. The largest gap occurs when the exponent is at its largest value and the least significant bit of the fraction changes. This gap is bM·b–s = bM–s.

As an example, consider a floating point representation in which there is a sign bit, a two-bit excess 2 exponent, and a three-bit normalized base 2 fraction in which the leading 1 is visible; that is, the leading 1 is not hidden. The representation of 0 is the bit pattern 000000. A number line showing all possible numbers that can be represented in this format is shown in Figure 2-9. Notice that there is

a relatively large gap between 0 and the first representable number, because the normalized representation does not support bit patterns that correspond to num- bers between 0 and the first representable number.

The smallest representable number occurs when the exponent and the fraction are at their smallest values. The smallest exponent is -2, and the smallest normal- ized fraction is (.100)2. The smallest representable number is then bm´b-1 = bm-1 = 2^-2-1 = 1/8.

Similarly, the largest representable number occurs when the exponent and the fraction are both at their largest values. The largest fraction occurs when the fraction is all 1’s, which is a number that is 2-3 less than 1 since there are three digits in the fraction. The largest representable number is then bM ´(1 – b–s) = 21 ´ (1 – 2-3) = 7/4.

The smallest gap occurs when the exponent is at its smallest value and the least significant bit of the fraction changes, which is bm´b–s = bm–s = 2-2-3 = 1/32.

Similarly, the largest gap occurs when the exponent is at its largest value and the least significant bit of the fraction changes, which is bM´b–s = bM–s = 21-3 = 1/4.

The number of bit patterns that represent valid numbers is less than the number of possible bit patterns, due to normalization. As discussed earlier, the number of representable numbers consists of five parts, which take into account the sign bit, the exponents, the first significant digit, the remaining digits, and the bit pattern for 0. This is computed as shown below:

Notice that the gaps are small for small numbers and that the gaps are large for large numbers. In fact, the relative error is approximately the same for all numbers. If we take the ratio of a large gap to a large number, and compare that to the ratio of a small gap to a small number, then the ratios are the same:

The representation for a “small number” is used here, rather than the smallest number, because the large gap between zero and the first representable number is a special case.

EXAMPLE

Consider the problem of converting (9.375 ´ 10-2)10 to base 2 scientific notation. That is, the result should have the form x.yy ´ 2z. We start by converting from

base 10 floating point to base 10 fixed point by moving the decimal point two positions to the left, which corresponds to the -2 exponent: .09375. We then convert from base 10 fixed point to base 2 fixed point by using the multiplication method:

2.3.5 THE IEEE 754 FLOATING POINT STANDARD

There are many ways to represent floating point numbers, a few of which we have already explored. Each representation has its own characteristics in terms of range, precision, and the number of representable numbers. In an effort to improve software portability and ensure uniform accuracy of floating point calculations, the IEEE 754 floating point standard for binary numbers was developed (IEEE, 1985). There are a few entrenched product lines that predate the standard that do not use it, such as the IBM/370, the DEC VAX, and the Cray line, but virtually all new architectures generally provide some level of IEEE 754 support.

The IEEE 754 standard as described below must be supported by a computer sys- tem, and not necessarily by the hardware entirely. That is, a mixture of hardware and software can be used while still conforming to the standard.

2.3.5.1Formats

There are two primary formats in the IEEE 754 standard: single precision and double precision. Figure 2-10 summarizes the layouts of the two formats. The

single precision format occupies 32 bits, whereas the double precision format occupies 64 bits. The double precision format is simply a wider version of the

single precision format.

The sign bit is in the leftmost position and indicates a positive or negative number for a 0 or a 1, respectively. The 8-bit excess 127 (not 128) exponent follows, in which the bit patterns 00000000 and 11111111 are reserved for special cases, as described below. For double precision, the 11-bit exponent is represented in excess 1023, with 00000000000 and 11111111111 reserved. The 23-bit base 2 fraction follows. There is a hidden bit to the left of the binary point, which when taken together with the single-precision fraction form a 23 + 1 = 24-bit significand of the form 1.fff…f where the fff…f pattern represents the 23-bit fractional part that is stored. The double-precision format also uses a hidden bit to the left of the binary point, which supports a 52 + 1 = 53 bit significand. For both for- mats, the number is normalized unless denormalized numbers are supported, as described later.

There are five basic types of numbers that can be represented. Nonzero normalized numbers take the form described above. A so-called “clean zero” is represented by the reserved bit pattern 00000000 in the exponent and all 0’s in the fraction. The sign bit can be 0 or 1, and so there are two representations for zero:

+0 and -0.

Infinity has a representation in which the exponent contains the reserved bit pat- tern 11111111, the fraction contains all 0’s, and the sign bit is 0 or 1. Infinity is useful in handling overflow situations or in giving a valid representation to a number (other than zero) divided by zero. If zero is divided by zero or infinity is divided by infinity, then the result is undefined. This is represented by the NaN (not a number) format in which the exponent contains the reserved bit pattern 11111111, the fraction is nonzero and the sign bit is 0 or 1. A NaN can also be produced by attempting to take the square root of -1.

As with all normalized representations, there is a large gap between zero and the first representable number. The denormalized, “dirty zero” representation allows numbers in this gap to be represented. The sign bit can be 0 or 1, the exponent contains the reserved bit pattern 00000000 which represents -126 for single pre- cision (-1022 for double precision), and the fraction contains the actual bit pat- tern for the magnitude of the number. Thus, there is no hidden 1 for this format. Note that the denormalized representation is not an unnormalized representation. The key difference is that there is only one representation for each denormalized number, whereas there are infinitely many unnormalized representations.

Figure 2-11 illustrates some examples of IEEE 754 floating point numbers.

Examples (a) through (h) are in single precision format and example (i) is in double precision format. Example (a) shows an ordinary single precision number. Notice that the significand is 1.101, but that only the fraction (101) is explicitly represented. Example (b) uses the smallest single precision exponent (–126) and example (c) uses the largest single precision exponent (127).

Examples (d) and (e) illustrate the two representations for zero. Example (f ) illustrates the bit pattern for +¥. There is also a corresponding bit pattern for –¥. Example (g) shows a denormalized number. Notice that although the number itself is 2-128, the smallest representable exponent is still -126. The exponent for single precision denormalized numbers is always -126, which is represented by the bit pattern 00000000 and a nonzero fraction. The fraction represents the magnitude of the number, rather than a significand. Thus we have +2-128 = +.01 ´ 2–126, which is represented by the bit pattern shown in Figure 2-11g.

Example (h) shows a single precision NaN. A NaN can be positive or negative. Finally, example (i) revisits the representation of 2–128 but now using double precision. The representation is for an ordinary double precision number and so there are no special considerations here. Notice that 2–128 has a significand of 1.0, which is why the fraction field is all 0’s.

In addition to the single precision and double precision formats, there are also single extended and double extended formats. The extended formats are not visible to the user, but they are used to retain a greater amount of internal precision during calculations to reduce the effects of roundoff errors. The extended formats increase the widths of the exponents and fractions by a number of bits that can vary depending on the implementation. For instance, the single extended format adds at least three bits to the exponent and eight bits to the fraction. The double extended format is typically 80 bits wide, with a 15-bit exponent and a 64-bit fraction.

2.3.5.2Rounding

An implementation of IEEE 754 must provide at least single precision, whereas the remaining formats are optional. Further, the result of any single operation on floating point numbers must be accurate to within half a bit in the least significant bit of the fraction. This means that some additional bits of precision may need to be retained during computation (referred to as guard bits), and there must be an appropriate method of rounding the intermediate result to the number of bits in the fraction.

There are four rounding modes in the IEEE 754 standard. One mode rounds to 0, another rounds toward +¥, and another rounds toward -¥. The default mode rounds to the nearest representable number. Halfway cases round to the number whose low order digit is even. For example, 1.01101 rounds to 1.0110 whereas 1.01111 rounds to 1.1000.