microcontrollers

Macros

If a stack based calling convention is used, then a number of registers may frequently need to be pushed and popped from the stack during calls and returns. In order to push ARC register %r15 onto the stack, we need to first decrement the stack pointer (which is in %r14) and then copy %r15 to the memory location pointed to by %r14 as shown in the code below:

The compact form assigns a new label (push) to the sequence of statements that actually carry out the command. The push label is referred to as a macro, and the process of translating a macro into its assembly language equivalent is referred to as macro expansion.

A macro can be created through the use of a macro definition, as shown for push in Figure 5-9. The macro begins with a .macro pseudo-op, and termi-

nates with a .endmacro pseudo-op. On the .macro line, the first symbol is the name of the macro (push here), and the remaining symbols are command line arguments that are used within the macro. There is only one argument for macro push, which is arg1. This corresponds to %r15 in the statement “push %r15,” or to %r1 in the statement “push %r1,” etc. The argument (%r15 or %r1) for each case is said to be “bound” to arg1 during the assembly process.

Additional formal parameters can be used, separated by commas as in:

The body of the macro follows the .macro pseudo-op. Any commands can fol- low, including other macros, or even calls to the same macro, which allows for a recursive expansion at assembly time. The parameters that appear in the .macro line can replace any text within the macro body, and so they can be used for labels, instructions, or operands.

It should be noted that during macro expansion formal parameters are replaced by actual parameters using a simple textual substitution. Thus one can invoke the push macro with either memory or register arguments:

The programmer needs to be aware of this feature of macro expansion when the macro is defined, lest the expanded macro contain illegal statements.

Additional pseudo-ops are needed for recursive macro expansion. The .if and .endif pseudo-ops open and close a conditional assembly section, respectively.

If the argument to .if is true (at macro expansion time) then the code that follows, up to the corresponding .endif, is assembled. If the argument to .if is false, then the code between .if and .endif is ignored by the assembler. The conditional operator for the .if pseudo-op can be any member of the set {<, =,.

Figure 5-10 shows a recursive macro definition and its expansion during the assembly process. The expanded code sums the contents of registers %r1 through %rX and places the result in %r1. The argument X is tested in the .if line. If X is greater than 2, then the macro is called again, but with the argument X – 1. If the macro recurs_add is invoked with an argument of 4, then three lines of

code are generated as shown in the bottom of the figure. The first time that recurs_add is invoked, X has a value of 4. The macro is invoked again with X = 3 and X = 2, at which point the first addcc statement is generated. The second and third addcc statements are then generated as the recursion unwinds.

As mentioned earlier, for an assembler that supports macros, there must be a macro expansion phase that takes place prior to the two-pass assembly process. Macro expansion is normally performed by a macro preprocessor before the program is assembled. The macro expansion process may be invisible to a programmer, however, since it may be invoked by the assembler itself. Macro expansion typically requires two passes, in which the first pass records macro definitions, and the second pass generates assembly language statements. The second pass of macro expansion can be very involved, however, if recursive macro definitions are supported. A more detailed description of macro expansion can be found in (Donovan, 1972).

5.2 Linking and Loading

Most applications of any size will have a number of separately compiled or assembled modules. These modules may be generated by different programming languages or they may be present in a library provided as part of the programming language environment or operating system. Each module must provide the information described above, so that they can be linked together for loading and execution.

A linkage editor, or linker, is a software program that combines separately assembled programs (called object modules) into a single program, which is called a load module. The linker resolves all global-external references and relocates addresses in the separate modules. The load module can then be loaded into memory by a loader, which may also need to modify addresses if the program is loaded at a location that differs from the loading origin used by the linker.

A relatively new technique called dynamic link libraries (DLLs), popularized by Microsoft in the Windows operating system, and present in similar forms in other operating systems, postpones the linking of some components until they are actually needed at run time. We will have more to say about dynamic linking later in this section.

5.3.1 LINKING

In combining the separately compiled or assembled modules into a load module, the linker must:

• Resolve address references that are external to modules as it links them.

• Relocate each module by combining them end-to-end as appropriate. During this relocation process many of the addresses in the module must be changed to reflect their new location.

• Specify the starting symbol of the load module.

• If the memory model includes more than one memory segment, the linker must specify the identities and contents of the various segments.

Resolving external references

In resolving address references the linker needs to distinguish local symbol names (used within a single source module) from global symbol names (used in more than one module). This is accomplished by making use of the .global and

.extern pseudo-ops during assembly. The .global pseudo-op instructs the assembler to mark a symbol as being available to other object modules during the linking phase. The .extern pseudo-op identifies a label that is used in one module but is defined in another. A .global is thus used in the module where a symbol is defined (such as where a subroutine is located) and a .extern is used in every other module that refers to it. Note that only address labels can be

global or external: it would be meaningless to mark a .equ symbol as global or external, since .equ is a pseudo-op that is used during the assembly process only, and the assembly process is completed by the time that the linking process begins.

All labels referred to in one program by another, such as subroutine names, will have a line of the form shown below in the source module:

.global symbol1, symbol2, …

All other labels are local, which means the same label can be used in more than one source module without risking confusion since local labels are not used after the assembly process finishes. A module that refers to symbols defined in another module should declare those symbols using the form:

.extern symbol1, symbol2, …

As an example of how .global and .extern are used, consider the two assembly code source modules shown in Figure 5-6. Each module is separately assem-

bled into an object module, each with its own symbol table as shown in Figure 5-7. The symbol tables have an additional field that indicates if a symbol is global or external. Program main begins at location 2048, and each instruction is four bytes long, so x and y are at locations 2064 and 2068, respectively. The symbol sub is marked as external as a result of the .extern pseudo-op. As part of the assembly process the assembler includes header information in the module about symbols that are global and external so they can be resolved at link time.

Relocation

Notice in Figure 5-6 that the two programs, main and sub, both have the same starting address, 2048. Obviously they cannot both occupy that same memory address. If the two modules are assembled separately there is no way for an assembler to know about the conflicting starting addresses during the assembly phase. In order to resolve this problem, the assembler marks symbols that may have their address changed during linking as relocatable, as shown in the Relocatable fields of the symbol tables shown in Figure 5-7. The idea is that a pro- gram that is assembled at a starting address of 2048 can be loaded at address 3000 instead, for instance, as long as all references to relocatable addresses within the program are increased by 3000 – 2048 = 952. Relocation is performed by the linker so that relocatable addresses are changed by the same amount that the loading origin is changed, but absolute, or non-relocatable addresses (such as the highest possible stack address, which is 231 – 4 for 32-bit words) stays the same regardless of the loading origin.

The assembler is responsible for determining which labels are relocatable when it builds the symbol table. It has no meaning to call an external label relocatable, since the label is defined in another module, so sub has no relocatable entry in the symbol table in Figure 5-7 for program main, but it is marked as relocatable in the subroutine library. The assembler must also identify code in the object module that needs to be modified as a result of relocation. Absolute numbers, such as constants (marked by .equ ,or that appear in memory locations, such as the contents of x and y, which are 105 and 92, respectively) are not relocatable. Memory locations that are positioned relative to a .org statement, such as x and y (not the contents of x and y!) are generally relocatable. References to fixed locations, such as a permanently resident graphics routine that may be hardwired into the machine, are not relocatable. All of the information needed to relocate a module is stored in the relocation dictionary contained in the assembled file, and is therefore available to the linker.

5.3.2 LOADING

The loader is a software program that places the load module into main memory. Conceptually the tasks of the loader are not difficult. It must load the various memory segments with the appropriate values and initialize certain registers such as the stack pointer %sp, and the program counter, %pc, to their initial values.

If there is only one load module executing at any time, then this model works well. In modern operating systems, however, several programs are resident in memory at any time, and there is no way that the assembler or linker can know at which address they will reside. The loader must relocate these modules at load time by adding an offset to all of the relocatable code in a module. This kind of loader is known as a relocating loader. The relocating loader does not simply repeat the job of the linker: the linker has to combine several object modules into a single load module, whereas the loader simply modifies relocatable addresses within a single load module so that several programs can reside in memory simultaneously. A linking loader performs both the linking process and the loading process: it resolves external references, relocates object modules, and loads them into memory.

The linked executable file contains header information describing where it should be loaded, starting addresses, and possibly relocation information, and entry points for any routines that should be made available externally.

An alternative approach that relies on memory management accomplishes relocation by loading a segment base register with the appropriate base to locate the code (or data) at the appropriate place in physical memory. The memory management unit (MMU), adds the contents of this base register to all memory references. As a result, each program can begin execution at address 0 and rely on the MMU to relocate all memory references transparently.

Dynamic link libraries

Returning to dynamic link libraries, the concept has a number of attractive features. Commonly used routines such as memory management or graphics pack- ages need be present at only one place, the DLL library. This results in smaller program sizes because each program does not need to have its own copy of the DLL code, as would otherwise be needed. All programs share the exact same code, even while simultaneously executing.

Furthermore, the DLL can be upgraded with bug fixes or feature enhancements in just one place, and programs that use it need not be recompiled or relinked in a separate step. These same features can also become disadvantages, however, because program behavior may change in unintended ways (such as running out of memory as a result of a larger DLL). The DLL library must be present at all times, and must contain the version expected by each program. Many Windows users have seen the cryptic message, “A file is missing from the dynamic link library.” Complicating the issue in the Windows implementation, there are a number of locations in the file system where DLLs are placed. The more sophisticated user may have little difficulty resolving these problems, but the naive user may be baffled.

A PROGRAMMING EXAMPLE

Consider the problem of adding two 64-bit numbers using the ARC assembly language. We can store the 64-bit numbers in successive words in memory and then separately add the low and high order words. If a carry is generated from adding the low order words, then the carry is added into the high order word of the result. (See problem 5.3 for the generation of the symbol table, and problem 5.4 for the translation of the assembly code in this example to machine code.)

Figure 5-8 shows one possible coding. The 64-bit operands A and B are stored in memory in a high endian format, in which the most significant 32 bits are stored in lower memory addresses than the least significant 32 bits. The program begins by loading the high and low order words of A into %r1 and %r2, respectively, and then loading the high and low order words of B into %r3 and %r4, respectively. Subroutine add_64 is called, which adds A and B and places the high order word of the result in %r5 and the low order word of the result in %r6. The 64-bit result is then stored in C, and the program returns.

Subroutine add_64 starts by adding the low order words. If a carry is not generated, then the high order words are added and the subroutine finishes. If a carry is generated from adding the low order words, then it must be added into the

high order word of the result. If a carry is not generated when the high order words are added, then the carry from the low order word of the result is simply added into the high order word of the result and the subroutine finishes. If, how- ever, a carry is generated when the high order words are added, then when the carry from the low order word is added into the high order word, the final state of the condition codes will show that there is no carry out of the high order word, which is incorrect. The condition code for the carry is restored by placing a large number in %r7 and then adding it to itself. The condition codes for n, z, and v may not have correct values at this point, however. A complete solution is not detailed here, but in short, the remaining condition codes can be set to their proper values by repeating the addcc just prior to the %r7 operation, taking into account the fact that the c condition code must still be preserved. ■

The Assembly Process

The process of translating an assembly language program into a machine language program is referred to as the assembly process. The assembly process is straightforward and rather simple, since there is a straightforward one-to-one mapping of assembly language statements to their machine language counter- parts. This is in opposition to compilation, for example, in which a given high-level language statement may be translated into a number of computation- ally equivalent machine language statements.

While assembly is a straightforward process, it is tedious and error-prone if done by hand. In fact, the assembler was one of the first software tools developed after the invention of the digital electronic computer.

Commercial assemblers provide at least the following capabilities:

• Allow the programmer to specify the run-time location of data values and programs. (Most often, however, the programmer would not specify an absolute starting location for a program, because the program will be moved around, or relocated, by the linker and perhaps the loader, as discussed be- low.)

• Provide a means for the programmer to initialize data values in memory prior to program execution.

• Provide assembly-language mnemonics for all machine instructions and ad- dressing modes, and translate valid assembly language statements into their equivalent machine language binary values.

• Permit the use of symbolic labels to represent addresses and constants.

• Provide a means for the programmer to specify the starting address of the program, if there is one. (There would not be a starting address if the mod- ule being assembled is a procedure or function, for example.)

• Provide a degree of assemble-time arithmetic.

• Include a mechanism that allows variables to be defined in one assembly language program and used in another, separately assembled program.

• Provide for the expansion of macro routines, that is, routines that can be defined once, and then instantiated as many times as needed.

We shall illustrate how the assembly process proceeds by “hand assembling” a simple program from ARC assembly language to ARC machine language. The program we will assemble is similar to Figure 4-13, reproduced below for convenience as Figure 5-1. In assembling this program we use the ARC encoding for-

mats shown in Figure 4-10, reproduced here as Figure 5-2. The figure shows the encoding of ARC machine language. That is, it specifies the target binary machine language of the ARC computer that the assembler must generate from the assembly language text.

Assembly and two pass assemblers

Most assemblers pass over the assembly language text twice, and are referred to as “two-pass assemblers.” The first pass is dedicated to determining the addresses of all data items and machine instructions, and selecting which machine instruction should be produced for each assembly language instruction (but not yet generating machine code).

The addresses of data items and instructions are determined by employing an assemble-time analog to the Program Counter, referred to as the location counter. The location counter keeps track of the address of the current instruction or data item as assembly proceeds. It is generally initialized to 0 at the start of the first pass, and is incremented by the size of each instruction. The .org pseudo operation causes the location counter to be set to the value specified by the .org statement. For example if the assembler encounters the statement

.org 1000

it would set the location counter to 1000, and the next instruction or data item would be assembled at that address. During this pass the assembler also performs any assembly-time arithmetic operations, and inserts the definitions of all labels and constant values into a table, referred to as the symbol table.

The primary reason for requiring a second pass is to allow symbols to be used in the program before they are defined, which is known as forward referencing. After the first pass, the assembler will have identified and entered all symbols into its symbol table, and, during a second pass generates the machine code, inserting the values of symbols which are then known.

Let us now hand assemble the program shown in Figure 5-1 into machine code. When the assembler encounters the first instruction,

it uses a pattern-matching process to recognize that it is a load instruction. Further pattern matching deduces that it is of the form “load from a memory address specified as a constant value (x in this case) plus the contents of a register (%r0 in this case) into a register (%r1 in this case).” This corresponds to the second Memory format shown in Figure 5-2. Examining the second Memory format we find that the op field for this instruction (ld) is 11. The destination of this ld instruction goes in the rd field, which is 00001 for %r1 in this case. The op3 field is 000000 for ld, as shown in the op3 box below the Memory formats. The rs1 field identifies the register, %r0 in this case, that is added to the simm13 field to form the source operand address. The i bit comes next. Notice that the i bit is used to distinguish between the first Memory format (i=0) and the second (i=0). Therefore the i bit is set to 1. The simm13 field specifies the address of the label x, which appears five words after the first instruction. Since the first instruction occurs at location 2048, and since each word is composed of four bytes, the address of x is 5 ´ 4 = 20 bytes after the beginning of the pro- gram. The address of x is then 2048 + 20 = 2068 which is represented by the bit pattern 0100000010100. This pattern fits into the signed 13-bit simm13 field.

The first line is thus assembled into the bit pattern shown below:

As a general approach, the assembly process is carried out by reading assembly language statements sequentially, from first to last, and generating machine code for each statement. And as mentioned earlier, a difficulty with this approach is caused by forward referencing. Consider the program fragment shown in Figure 5-3. When the assembler sees the call statement, it does not yet know the loca-

tion of sub_r since the sub_r label has not yet been seen. Thus the reference is entered into the symbol table and marked as unresolved. The reference is resolved when the definition of sub_r is found later in the program. The process of building a symbol table is described below.

Assembly and the symbol table

In the first pass of the two-pass assembly process, a symbol table is created. A symbol is either a label or a symbolic name that refers to a value used during the assembly process. The symbol table is generated in the first pass of assembly.

As an example of how a two-pass assembler operates, consider assembling the code in Figure 4-14. Starting from the .begin statement, the assembler encounters the statement

.org 2048

This causes the assembler to set the location counter to 2048, and assembly proceeds from that address. The first statement encountered is

a_start .equ 3000

An entry is created in the symbol table for a_start, which is given the value 3000. (Note that .equ statements do not generate any code, and thus are not assigned addresses during assembly.)

Assembly proceeds as the assembler encounters the first machine instruction,

This instruction is assembled at the address specified by the location counter, 2048. The location counter is then incremented by the size of the instruction, 4 bytes, to 2052. Notice that when the symbol length is encountered the assembler has not seen any definition for it. An entry is created in the symbol table for length, but it is initially assigned the value “undefined” as shown by the “—” in Figure 5-4a.

The assembler then encounters the second instruction

It assembles this instruction at address 2052 and enters the symbol address into the symbol table, again setting its value to “undefined,” since its definition has not been seen. It then increments the location counter by 4 to 2056. The andcc instruction is assembled at address 2056, and the location counter is incremented by the size of the instruction, again 4 bytes, to 2060. The next symbol that is seen is loop, which is entered into the symbol table with a value of 2060, the value of the location counter. The next symbol that is encountered that is not in the symbol table is done, which is also entered into the symbol table without a value since it likewise has not been defined.

The first pass of assembly continues, and the unresolved symbols length, address, and done are assigned the values 2092, 2096, and 2088, respectively as they are encountered. The label a is encountered, and is entered into the table with a value of 3000. The label done appears at location 2088 because there are 10 instructions (40 bytes) between the beginning of the program and done. Addresses for the remaining labels are computed in a similar manner. If any labels are still undefined at the end of the first pass, then an error exists in the program and the assembler will flag the undefined symbols and terminate.

After the symbol table is created, the second pass of assembly begins. The pro- gram is read a second time, starting from the .begin statement, but now object code is generated. The first statement that is encountered that causes code to be generated is ld at location 2048. The symbol table shows that the address portion of the ld instruction is (2092)10 for the address of length, and so one word of code is generated using the Memory format as shown in Figure 5-5. The second pass continues in this manner until all of the code is translated. The assembled program is shown in Figure 5-5. Notice that the displacements for branch addresses are given in words, rather than in bytes, because the branch instructions multiply the displacements by four.

Final tasks of the assembler

After assembly is complete the assembler must add additional information to the assembled module for the linker and loader:

• The module name and size. If the execution model involves memory seg-

ments for code, data, stack, etc. then the sizes and identities of the various segments must be specified.

• The address of the start symbol, if one is defined in the module. Most assemblers and high level languages provide for a special reserved label that the programmer can use to indicate where the program should start execution. For example, C specifies that execution will start at the function named main(). In Figure 5-1 the label “main” is a signal to the assembler that execution should start at that location.

• Information about global and external symbols. The linker will need to know the addresses of any global symbols defined in the module and ex- ported by it, and it will likewise need to know which symbols remain un- defined in the module because they are defined as global in another module.

• Information about any library routines that are referenced by the module. Some libraries contain commonly used functionality such as math or other specialized functions. We will have more to say about library usage in the sections below.

• The values of any constants that are to be loaded into memory. Some loaders expect data initialization to be specified separately from the binary code.

• Relocation information. When the linker is invoked most of the modules that are to be linked will need to be relocated as the modules are concatenated. The whole issue of module relocation is complicated because some address references can be relocated and others cannot. We discuss relocation later, but here we note that the assembler specifies which addresses can be relocated and which others cannot.

Location of programs in memory

Up until now we have assumed that programs are located in memory at an address that is specified by a .org pseudo operation. This may indeed be the case in systems programming, where the programmer has a reason for wanting a program to be located at a specific memory location, but typically the programmer does not care where the program is located in memory. Furthermore, when separately assembled or compiled programs are linked together, it is difficult or impossible for the programmer to know exactly where each module will be located after linking, as they are concatenated one after the other. For this reason most addresses are specified as being relocatable in memory, except perhaps for addresses such as I/O addresses, which may be fixed at an absolute memory location.

In the next section we discuss relocation in more detail; here we merely note that it is the assembler’s responsibility to mark symbols as being relocatable. Whether a given symbol is relocatable or not depends upon both the assembly language and the operating system’s conventions. In any case, this relocation information is included in the assembled module for use by the linker and/or loader in a relocation dictionary. Symbols that are relocatable are often marked with an “R” after their value in the assembler’s listing file.

LANGUAGES AND THE MACHINE

In the last chapter we looked at the relationship between the ISA, the assembly language, and machine language. We also saw in some detail how instructions effected register transfers and the movement of data between memory and the CPU, but we touched only briefly on the actual process of assembly and program linking and loading. In this chapter we widen our view of the relationships between computer languages and the machine.

We begin by discussing compilation, the process of translating a program writ- ten in a high level language into a functionally equivalent program in assembly language. Following that, we discuss the process of assembly, the translation of an assembly language program into a functionally equivalent machine language program. We then discuss linking, the process of linking together separately assembled modules into a single program, and loading, the process of moving programs into memory and preparing them for execution. Following that, we discuss the use of assembly language macros, which can be thought of as akin to assembly-time procedures, with the exception that they are placed inline, or expanded, in the assembly language program at every location where they are invoked.

5.1 The Compilation Process

As we will see later in the chapter, the process of assembling an assembly language program into machine code is rather straightforward, because there is a one to one mapping between assembly language statements and the equivalent machine binary codes. High-level languages, on the other hand, present a much more complex problem.

5.1.1 THE STEPS OF COMPILATION

Consider a simple assignment statement

A = B + 4;

The compiler is faced with a number of fairly complex tasks in converting this statement into one or more assembly language statements:

• Reducing the program text to the basic symbols of the language, for example into identifiers such as A and B, denotations such as the constant value 4, and program delimiters such as = and +. This portion of compilation is referred to as lexical analysis.

• Parsing the symbols to recognize the underlying program structure. In the sample statement above, for example, the parser must recognize the statement as being an assignment statement of the form

 Identifier “=” Expression,

where Expression is further parsed into the form

 Identifier “+” Constant.

Parsing is sometimes called syntactic analysis.

• Name analysis: associating the names A and B with particular program variables, and further associating them with particular memory locations where the variables will be located at run time.

• Type analysis: determining the type of all data items. In the case above, the variables A and B, and constant 4 would be recognized as being of type int in some languages. Name and type analysis are sometimes referred to together as semantic analysis: determining the underlying meaning of pro- gram components.

• Action mapping and code generation: associating program statements with their appropriate assembly language sequence. In the statement above, the assembly language sequence might be as follows:

• There are additional steps that the compiler must take such as allocating variables to registers, tracking register usage, and, should the programmer desire it, optimizing the program.

5.1.2 THE COMPILER MAPPING SPECIFICATION

When the compiler itself is being created, information about the particular ISA must be embedded into it. (Note that the ISA on which the compiler executes does not need to be the same as the ISA code that the compiler generates, a process known as cross compilation.) This embedding is sometimes called the mapping specification for the compiler. For example, the compiler writer must decide how to map variables and constants of various types into the machine’s resources. This may be a function of both the machine and the high level language. In the C language, for example, integers (ints) can be 16, 32, or some other number of bits in size, while Java specifies that all ints be 32-bits in size. The example in the previous section, if considered for the C language, maps integers to ARC 32-bit words.

The compiler writer must also take into account the features and limitations of the machine when mapping high level language constructs to assembly language statements or statement sequences. For example, the ARC instruction set requires that all arithmetic operands must be either immediate constants or register variables. Therefore the compiler must generate code to get all variables into registers before any arithmetic instructions can be executed. This is the reason for the instruction:

in the example above.

In this text we concentrate on the mapping of common high level language constructs to their equivalent assembly language constructs, leaving the details of lexical and syntactic and semantic analysis to compiler texts. (Several compiler texts are described in the Further Reading section at the end of this chapter for the interested reader.)

5.1.3 HOW THE COMPILER MAPS THE THREE INSTRUCTION CLASSES INTO ASSEMBLY CODE

Let us consider in detail the mapping of the three instruction classes: data movement, arithmetic, and control flow, from high level language into assembly language. In the discussion and examples below we will use C as the example language. We choose C because of its popularity, and because its syntax and semantics, while certainly high level, are still fairly close to assembly language concepts. The reader who is unfamiliar with C should not be distracted by this choice; the syntax and semantics of C are easy to understand and carry over to other high level languages.

Variable storage in memory

In the example above, and in most of the programming examples in this text, it has been assumed that variables can be accessed directly by their name, which is mapped to a memory location that is known at the time the program is assembled, sometimes called “assembly time.” In the example above, A = B + 4, it is assumed that the variables A and B have addresses that are known when the statement is compiled. In fact, only global variables, known as static variables in C, have addresses that are known at compile time. Variables declared inside of functions or inside of blocks that are not explicitly declared as static or global only come into existence when the function or block is entered, and they disappear when the function or block is exited for the last time. These variables are called local, or in C, automatic variables. In most programs, local variables are actually much more common than global variables.

Given this ephemeral nature of local variables, a natural way of implementing them is on a last-in-first-out stack as described in Chapter 4. Variables that are stored on the stack come into existence when the stack frame is created and the function is called, and they disappear when the function is exited for the last time. While the previous chapter employed the stack pointer, %sp, to access the stack frame, it is also common to copy the contents of %sp into another register called the frame pointer %fp (also known as the base pointer) upon entry into the function, and then to use %fp to access variables on the stack frame for the duration of the function’s life. This is because temporary variables may be continually pushed and popped onto and off of the stack during the lifetime of the function, resulting in a changing offset between %sp and the items on the stack frame. Using %fp means that the compiler can define a constant offset between %fp and a value stored on the stack that will remain fixed for the life of the frame. Based addressing is used to access stack variables. For example, an ARC variable located on the stack at a location 12 bytes below %fp can loaded into register %r1 by the instruction

The use of based addressing thus allows the address arithmetic, “add the contents of %fp to -12” to be performed in a single instruction. Based addressing is so common that all popular instruction sets contain that addressing mode. Some instruction sets contain even more complicated addressing modes to assist in accessing complex data structures that are stored in the stack frame.

To emphasize the point, variables that are stored on the stack have memory addresses that are not known until run time. Their compile time addresses are known as offsets from %fp. It is only at function entry time that the actual memory address of the value is known. Thus even though stack variable addresses such as [%fp – 12] are much more common than global variable addresses such as A, we will assume global variables are used in the discussion below because of the greater ease in understanding the relationship between the high level language variable name and the address as specified in assembly language. With that provision, let us now proceed to discuss three classes of program statements: data movement, arithmetic, and control flow.

5.1.4 DATA MOVEMENT

In addition to simple scalar variables, most programming languages provide vari- ous kinds of more complex data structures, including fixed record structures such as the C struct data type, which is similar to the Pascal record, and the array data type common to most programming languages.

Structures

An example of a C struct is the representation of a point in 3-dimensional space having integer coordinates x, y, and z. In C this structure could be declared as:

An instance of this struct would be defined by the C statement

struct point pt;

Having defined point pt, the programmer can now refer to the individual components of pt by notation such as pt.x, which refers to the x component of struct pt. The compiler would lay out this structure in memory as three consecutive memory locations.

The memory address of the entire structure is taken to be the lowest, or base address of the structure, so the x component would be located at address pt, the y component at address pt + 4, and the z component at address pt + 8. Thus the y component of pt would be loaded into register %r1 by the instruction

Arrays

Most programming languages also allow the declaration of arrays of objects, that is, collections of identical components that can be referred to either individually or collectively. In C an array of ten integers can be defined with:

int A[10];

This definition would result in a collection of ten integers, indexed from 0 to 9.

The components of a struct must be explicitly named at programming time, for example, pt.z. References such as pt.i where i is a variable whose name is not determined until run time are not allowed. With arrays, on the other hand, the array index can be computed at run time. For example, the programmer may specify array element A[i], where i is a variable whose value is computed at run time and which may assume any integer value from 0 through 9. Whereas in C the index of the first element in the array always has an index of 0, other programming languages allow more flexibility. In Pascal, for example, array declarations such as:

A: array [-10..10] of integer

are permitted. This declaration would result in an array of 21 integers with indices running from -10 to +10.

Accessing array elements presents a more complicated issue because of this need to compute the index at run time, and the possibility that indices may not begin with 0. The general expression for computing the machine address of an array element at run time is given by:

where BASE is the starting address of the array, INDEX is the index of the desired element, START is the starting index of the array, and SIZE is the size of an individual element in bytes. Thus element 5 in the Pascal array declared above would have an address of A + (5 – (-10))*4 = A + 60. In ARC assembly language, assuming BASE in %r2, INDEX in %r3, START in %r4, and assuming SIZE = 4, the code to load an array value into memory would be given by

(sll is “shift left logical,” which shifts %r6 2 bits to the left is this example, bringing in two 0’s on the right.) Note that it costs three instructions to access an array element, and more if SIZE is not a power of 2. Also note that in the C programming language, which specifies that START = 0, one machine instruction is saved for each array access. This may result in a considerable savings in scientific and engineering calculations, where heavy array references are common.

5.1.5 ARITHMETIC INSTRUCTIONS

Arithmetic instructions are mapped pretty much as expected from their usage. There is a possible complication in load-store machines such as ARC and commercial RISC machines, however. Regardless of how many registers with which a machine is endowed, there is always the possibility that the compiler will encounter an arithmetic instruction that requires more registers than are avail- able. In this case the compiler must temporarily store variables on the stack, a so-called “register spill.” Compilers use sophisticated techniques to decide which registers are available, using a graph-theoretic technique known as register coloring, and to decide when the value in a register is no longer needed to store a particular value, which is known as “live-dead analysis.”

5.1.6 PROGRAM CONTROL FLOW

Most ISAs use unconditional and conditional branches, and the CPU’s arithmetic flags to implement program control flow structures. In this section we con- sider the mapping of the most common control flow statements.

The goto statement

The most trivial control flow statement is the goto statement, goto Label, which is simply implemented by the ba (branch always) unconditional branch:

which has the meaning, “If expr yields a value of true, execute stmt1, other- wise execute stmt2.” Thus the compiler must evaluate the truth of expr, and execute one or the other of the two statements depending upon the truth or falsity of the expression. Assume for brevity in the example below that expr is (%r1 == %r2), and introducing the bne, branch if not equal instruction, then the code to implement the if-else statement is:

Note that the sign of the conditional branch, bne, branch if not equal, is the inverse of the expression, (%r1 == %r2), equals. This is because the code falls through to the stmt1 code if the condition is met, and must branch around this code if the condition is not met.

The while statement

The C while statement has the syntax:

while (expr) stmt;

The statement means, “Evaluate expr. If it is true, execute stmt, and repeat this process until expr evaluates to false.” The assembly language mapping of this statement has the interesting feature that the most efficient mapping has the expression evaluation code following the statement code. Consider the C while statement:

where again we use register variables to simplify the code. This statement is effi- ciently implemented as:

The reader can verify that placing the expression evaluation code below the statement code is more efficient than having the expression evaluation code above the statement code.

The do-while statement

C also has a do-while statement with the syntax:

do stmt while (expr);

This statement works like the while statement above except that stmt is always executed once prior to testing expr. It is implemented exactly like the while statement above except that the first ba instruction is eliminated.

The for statement

The C for statement has the syntax:

for (expr1; expr2; expr3) stmt;

The C language definition says that this statement is equivalent to:

Thus it is implemented exactly like the while statements above, with the addition of code for expr1 and expr3.

■ SUMMARY

In this chapter, we introduced the ARC ISA, and studied some general properties of ISAs. In the design of an instruction set, a balance must be struck between sys- tem performance and the characteristics of the technology in which the processor is implemented. Interaction between the CPU and the memory is a key consideration.

When a memory access is made, the way in which the address is calculated is called the memory addressing mode. We examined the sequence of computations that can be combined to make up an addressing mode. We also looked at some specific cases which are commonly identified by name.

We also looked at several parts of a computer system that play a role in the execution of a program. We learned that programs are made up of sequences of instructions, which are taken from the instruction set of the CPU. In the next chapter, we will study how these sequences of instructions are translated into object code.

■ FURTHER READING

The material in this chapter is for the most part a collection of the historical experience gained in fifty years of stored program computer designs. Although each generation of computer systems is typically identified by a specific hardware technology, there have also been historically important instruction set architectures. In the first generation systems of the 1950’s, such as Von Neuman’s EDVAC, Eckert and Mauchly’s UNIVAC and the IBM 701, programming was performed by hand in machine language. Although simple, these instruction set architectures defined the fundamental concepts surrounding opcodes and operands.

The concept of an instruction set architecture as an identifiable entity can be traced to the designers of the IBM S/360 in the 1960’s. The VAX architecture for Digital Equipment Corporation can also trace its roots to this period when the minicomputers, the PDP-4 and PDP-8 were being developed. Both the 360 and VAX are two-address architectures. Significant one-address architectures include the Intel 8080 which is the predecessor to the modern 80×86, and its contemporary at that time: the Zilog Z-80. As a zero-address architecture, the Burroughs B5000 is also of historical significance.

There are a host of references that cover the various machine languages in existence, too many to enumerate here, and so we mention only a few of the more celebrated cases. The machine languages of Babbage’s machines are covered in (Bromley, 1987). The machine language of the early Institute for Advanced Study (IAS) computer is covered in (Stallings, 1996). The IBM 360 machine language is covered in (Strubl, 1975). The machine language of the 68000 can be found in (Gill, 1987) and the machine language of the SPARC can be found in (SPARC, 1992). A full description of the JVM and the Java class file format can be found in (Meyer & Downing, 1997.)

Bromley, A. G., “The Evolution of Babbage’s Calculating Engines,” Annals of the History of Computing, 9, pp. 113-138, (1987).

Gill, A., E. Corwin, and A. Logar, Assembly Language Programming for the 68000, Prentice-Hall, Englewood Cliffs, New Jersey, (1987).

Meyer, J. and T. Downing, Java Virtual Machine, O’Reilly & Associates, Sebastopol, California, (1997).

SPARC International, Inc., The SPARC Architecture Manual: Version 8, Prentice Hall, Englewood Cliffs, New Jersey, (1992).

Stallings, W., Computer Organization and Architecture, 4/e, Prentice Hall, Upper Saddle River, (1996).

Struble, G. W., Assembler Language Programming: The IBM System/360 and 370, 2/e, Addison-Wesley, Reading, (1975).

■ PROBLEMS

4.1 A memory has 224 addressable locations. What is the smallest width in bits that the address can be while still being able to address all 224 locations?

4.2 What are the lowest and highest addresses in a 220 byte memory, in which a four-byte word is the smallest addressable unit?

4.3 The memory map for the ARC is shown in Figure 4-20.

(a) How much memory (in bytes) is available for each of the add-in video memory modules? (Give your answer as powers of two or sums of powers of two, e.g. 210.)

(b) When a finger is drawn across the touchscreen, the horizontal (x) and ver- tical (y) positions of the joystick are updated in registers that are accessed at locations (FFFFF0)16 and (FFFFF4)16, respectively. When the number ‘1’ is written to the register at memory location (FFFFEC)16 the screen flashes, and then location (FFFFEC)16 is automatically cleared to zero by the hardware (the software does not have to clear it). Write an ARC program that flashes the screen every time the user’s position changes. Use the skeleton program shown below.

4.4 Write an ARC subroutine that performs a swap operation on the 32-bit operands x = 25 and y = 50, which are stored in memory. Use as few registers as you can.

4.5 A section of ARC assembly code is shown below. What does it do? Express your answer in terms of the actions it goes through. Does it add up numbers, or clear something out? Does it simulate a for loop, a while loop, or some- thing else? Assume that a and b are memory locations that are defined else- where in the code.

4.6 A pocket pager contains a small processor with 27 8-bit words of memory.

The ISA has four registers: R0, R1, R2, and R3. The instruction set is shown in Figure 4-27, as well as the bit patterns that correspond to each register, the

instruction format, and the modes, which determine if the operand is a register (mode bit = 0) or the operand is a memory location (mode bit = 1). Either or both of the operands can be registers, but both operands cannot be memory locations. If the source or destination is a memory location, then the corresponding source or destination field in the instruction is not used since the address field is used instead.

(a) Write a program using object code (not assembly code) that swaps the con- tents of registers R0 and R1. You are free to use the other registers as necessary, but do not use memory. Use no more than four lines of code (fewer lines are possible). Place 0’s in any positions where the value does not matter.

(b) Write a program using object code that swaps the contents of memory

locations 12 and 13. As in part (a), you are free to use the other registers as necessary, but do not use other memory locations. Place 0’s in any positions where the value does not matter.

4.7 An ARC program calls the subroutine foo, passing it three arguments, a, b, and c. The subroutine has two local variables, m and n. Show the position of the stack pointer and the contents of the relevant stack elements for a stack based calling convention at the points in the program shown below. Note that subroutine foo does not return anything.

4.8 Why does sethi only load the high 22 bits of a register? It would be more useful if sethi loaded all 32 bits of a register. What is the problem with having sethi load all 32 bits?

4.9 Which of the three subroutine linkage conventions covered in this chapter (registers, data link area, stack) is used in Figure 4-14?

4.10 A program compiled for a SPARC ISA writes the 32-bit unsigned integer 0xABCDEF01 to a file, and reads it back correctly. The same program com-

piled for a Pentium ISA also works correctly. However, when the file is trans- ferred between machines, the program incorrectly reads the integer from the file as 0x01EFCDAB. What is going wrong?

4.11 Refer to Figure 4-25. Show the Java assembly language instructions for the code shown in locations 0x011e – 0x0122. Use the syntax format shown in locations 0x00e3 – 0x0ef of that same figure.

You will need to make use of the following Java instructions:

invokespecial n (opcode 0xb7) – Invoke a method with index n into the constant pool. Note that n is a 16-bit (two-byte) index that follows the invokespecial opcode.

aload_0 (opcode 0x2a) – Push local variable 0 onto the stack.

4.12 Is the JVM a little-endian or big-endian machine? Hint: Examine the first line of the bytecode program in Figure 4-24.

4.13 Write an ARC program that implements the bytecode program shown in Figure 4-26. Assume that, analogous in the code in the figure, the arguments are passed on a stack, and that the return value is placed on the top of the stack.

4.14 A JVM is implemented using the ARC ISA.

a) How much memory traffic will be generated when the program of Figure 4-26 executes?

b) For exercise 4-13, compute the memory traffic your program will generate. Then, for part (a) above, compare that traffic with the amount generated by your program. If most of the execution time of a program is due to its memory accesses, how much faster will your program be compared to the program in Figure 4-26?

4.15 Can a Java bytecode program ever run as fast as a program written in the native language of the processor? Defend your answer in one or two paragraphs.

4.16 (a) Write three-address, two-address, and one-address programs to compute the function A = (B-C)*(D-E). Assume 8-bit opcodes, 16-bit operands and addresses, and that data is moved to and from memory in 16-bit chunks. (Also assume that the opcode must be transferred from memory by itself.) Your code should not overwrite any of the operands. Use any temporary registers needed.

(b) Compute the size of your program in bytes.

(c) Compute the memory traffic your program will generate at execution time, including instruction fetches.

4.17 Repeat Exercise 4.16 above, using ARC assembly language. Note that the subtract mnemonic is subcc and that the multiplication mnemonic is smul.

Input and Output in Assembly Language

Finally, we come to ways in which an assembly language program can communicate with the outside world: input and output (I/O) activities. One way that communication between I/O devices and the rest of the machine can be handled is with special instructions, and with a special I/O bus reserved for this purpose. An alternative method for interacting with I/O devices is through the use of memory mapped I/O, in which devices occupy sections of the address space where no ordinary memory exists. Devices are accessed as if they are memory locations, and so there is no need for handling devices with new instructions.

As an example of memory mapped I/O, consider again the memory map for the ARC, which is illustrated in Figure 4-20. We see a few new regions of memory,

for two add-in video memory modules and for a touchscreen. A touchscreen comes in two forms, photonic and electrical. An illustration of the photonic version is shown in Figure 4-21. A matrix of beams covers the screen in the horizon-

tal and vertical dimensions. If the beams are interrupted (by a finger for example) then the position is determined by the interrupted beams. (In an alternative version of the touchscreen, the display is covered with a touch sensitive surface. The user must make contact with the screen in order to register a selection.)

The only real memory occupies the address space between 222 and 223 – 1. (Remember: 223 – 4 is the address of the leftmost byte of the highest word in the big-endian format.) The rest of the address space is occupied by other components. The address space between 0 and 216 – 1 (inclusive) contains built-in pro- grams for the power-on bootstrap operation and basic graphics routines. The address space between 216 and 219 – 1 is used for two add-in video memory modules, which we will study in Problem Figure 4.3. Note that valid information is available only when the add-in memory modules are physically inserted into the machine.

Finally, the address space between 223 and 224 – 1 is used for I/O devices. For this system, the X and Y coordinates that mark the position where a user has made a selection are automatically updated in registers that are placed in the memory map. The registers are accessed by simply reading from the memory locations where these registers are located. The “Screen Flash” location causes the screen to flash whenever it is written.

Suppose that we would like to write a simple program that flashes the screen whenever the user changes position. The flowchart in Figure 4-22 illustrates how this might be done. The X and Y registers are first read, and are then compared with the previous X and Y values. If either position has changed, then the screen is flashed and the previous X and Y values are updated and the process repeats. If neither position has changed, then the process simply repeats. This is an example of the programmed I/O method of accessing a device. (See problem 4.3 at the end of the chapter for a more detailed description.)

Case Study: The Java Virtual Machine ISA

Java is a high-level programming language developed by Sun Microsystems that has taken a prominent position in the programming community. A key aspect of Java is that Java binary codes are platform-independent, which means that the same compiled code can run without modification on any computer that sup- ports the Java Virtual Machine (JVM). The JVM is how Java achieves its plat- form-independence: a standard specification of the JVM is implemented in the native instruction sets of many underlying machines, and compiled Java codes can then run in any JVM environment.

Programs that are written in fully compiled languages like C, C++, and Fortran, are compiled into the native code of the target architecture, and are generally not portable across platforms unless the source code is recompiled for the target

machine. Interpreted languages, like Perl, Tcl, AppleScript, and shell script, are largely platform independent, but can execute 100 to 200 times slower than a fully compiled language. Java programs are compiled into an intermediate form known as bytecodes, which execute on the order of 10 times more slowly than fully compiled languages, but the cross-platform compatibility and other language features make Java a favorable programming language for many applications.

A high level view of the JVM architecture is shown in Figure 4-23. The JVM is a stack-based machine, which means that the operands are pushed and popped from a stack, instead of being transferred among general purpose registers. There are, however, a number of special purpose registers, and also a number of local variables that serve the function of general purpose registers in a “real” (non-virtual) architecture. The Java Execution Engine takes compiled Java bytecodes at its input, and interprets the bytecodes in a software implementation of the JVM, or executes the bytecodes directly in a hardware implementation of the JVM.

Figure 4-24 shows a Java implementation of the SPARC program we studied in Figure 4-13. The figure shows both the Java source program and the bytecodes into which it was compiled. The bytecode file is known as a Java class file (which is what a compiled Java program is called.)

Only a small number of bytes in a class file actually contain instructions; the rest is overhead that the file must contain in order to run on the JVM. In Figure 4-25 we have “disassembled” the bytecodes back to their higher-level format. The bytecode locations are given in hexadecimal, starting at location 0x00. The first 4 bytes contain the magic number 0xcafebabe which identifies the program as a compiled Java class file. The major version and minor version numbers refer to the Java runtime system for which the program is compiled. The number of entries in the constant pool follows, which is actually 17 in this example: the first entry (constant pool location 0) is always reserved for the JVM, and is not included in the class file, although indexing into the constant pool starts at location 0 as if it is explicitly represented. The constant pool contains the names of methods (functions), attributes, and other information used by the runtime sys-

The remainder of the file is mostly composed of the constant pool, and executable Java instructions. We will not cover all details of the Java class file here. The reader is referred to (Meyer & Downing, 1997) for a full description of the Java class file format.

The actual code that corresponds to the Java source program, which simply adds the constants 15 and 9, and returns the result (24) to the calling routine on the stack, appears in locations 0x00e3 – 0x00ef. Figure 4-26 shows how that portion of the bytecode is interpreted. The program pushes the constants 15 and 9 onto the stack, using local variables 0 and 1 as intermediaries, and invokes the iadd instruction which pops the top two stack elements, adds them, and places the result on the top of the stack. The program then returns.

A cursory glance at the code shows some of the reasons why the JVM runs 10 times slower than native code. Notice that the program stores the arguments in

local variables 1 and 2, and then transfers them to the Java stack before adding them. This transfer would be viewed as redundant by native code compilers for other languages, and would be eliminated. Given this example alone, there is probably considerable room for speed improvements from the 10´ slower execu-

tion time of today’s JVMs. Other improvements may also come in the form of just in time (JIT) compilers. Rather than interpreting the JVM bytecodes one by one into the target machine code each time they are encountered, JIT compilers take advantage of the fact that most programs spend most of their time in

loops and other iterative routines. As the JIT encounters each line of code for the first time, it compiles it into native code and stores it away in memory for possible later use. The next time that code is executed, it is the native, compiled form that is executed rather than the bytecodes.

Accessing Data in Memory— Addressing Modes

Up to this point, we have seen four ways of computing the address of a value in memory: (1) a constant value, known at assembly time, (2) the contents of a register, (3) the sum of two registers, and (4) the sum of a register and a constant.

Table 4.1 gives names to these addressing modes, and shows a few others as well. Notice that the syntax of the table differs from that of the ARC. This is a common, unfortunate feature of assembly languages: each one differs from the rest in its syntax conventions. The notation M[x] in the Meaning column assumes memory is an array, M, whose byte index is given by the address computation in brackets. There may seem to be a bewildering assortment of addressing modes, but each has its usage:

• Immediate addressing allows a reference to a constant that is known at assembly time.

• Direct addressing is used to access data items whose address is known at assembly time.

• Indirect addressing is used to access a pointer variable whose address is known at compile time. This addressing mode is seldom supported in modern processors because it requires two memory references to access the operand, making it a complicated instruction. Programmers who wish to access data in this form must use two instructions, one to access the pointer and another to access the value to which it refers. This has the beneficial side effect of exposing the complexity of the addressing mode, perhaps discouraging its use.

• Register indirect addressing is used when the address of the operand is not known until run time. Stack operands fit this description, and are accessed by register indirect addressing, often in the form of push and pop instructions that also decrement and increment the register respectively.

• Register indexed, register based, and register based indexed addressing are used to access components of arrays such as the one in Figure 4-14, and components buried beneath the top of the stack, in a data structure known as the stack frame, which is discussed in the next section.

Subroutine Linkage and Stacks

A subroutine, sometimes called a function or procedure, is a sequence of instructions that is invoked in a manner that makes it appear to be a single instruction in a high level view. When a program calls a subroutine, control is passed from the program to the subroutine, which executes a sequence of instructions and then returns to the location just past where it was called. There are a number of methods for passing arguments to and from the called routine, referred to as calling conventions. The process of passing arguments between routines is referred to as subroutine linkage.

One calling convention simply places the arguments in registers. The code in Figure 4-15 shows a program that loads two arguments into %r1 and %r2, calls

subroutine add_1, and then retrieves the result from %r3. Subroutine add_1 takes its operands from %r1 and %r2, and places the result in %r3 before returning via the jmpl instruction. This method is fast and simple, but it will not work if the number of arguments that are passed between the routines exceeds the number of free registers, or if subroutine calls are deeply nested.

A second calling convention creates a data link area. The address of the data link area is passed in a predetermined register to the called routine. Figure 4-16 shows

an example of this method of subroutine linkage. The .dwb pseudo-op in the calling routine sets up a data link area that is three words long, at addresses x, x+4, and x+8. The calling routine loads its two arguments into x and x+4, calls subroutine add_2, and then retrieves the result passed back from add_2 from memory location x+8. The address of data link area x is passed to add_2 in register %r5.

Note that sethi must have a constant for its source operand, and so the assembler recognizes the sethi construct shown for the calling routine and replaces x with its address. The srl that follows the sethi moves the address x into the least significant 22 bits of %r5, since sethi places its operand into the leftmost 22 bits of the target register. An alternative approach to loading the address of x into %r5 would be to use a storage location for the address of x, and then simply apply the ld instruction to load the address into %r5. While the latter approach is simpler, the sethi/srl approach is faster because it does not involve a time consuming access to the memory.

Subroutine add_2 reads its two operands from the data link area at locations %r5 and %r5 + 4, and places its result in the data link area at location %r5 + 8 before returning. By using a data link area, arbitrarily large blocks of data can be passed between routines without copying more than a single register during subroutine linkage. Recursion can create a burdensome bookkeeping overhead, however, since a routine that calls itself will need several data link areas. Data link areas have the advantage that their size can be unlimited, but also have the disadvantage that the size of the data link area must be known at assembly time.

A third calling convention uses a stack. The general idea is that the calling rou- tine pushes all of its arguments (or pointers to arguments, if the data objects are large) onto a last-in-first-out stack. The called routine then pops the passed arguments from the stack, and pushes any return values onto the stack. The calling routine then retrieves the return value(s) from the stack and continues execution. A register in the CPU, known as the stack pointer, contains the address of the top of the stack. Many machines have push and pop instructions that automatically decrement and increment the stack pointer as data items are pushed and popped.

An advantage of using a stack is that its size grows and shrinks as needed. This supports arbitrarily deep nesting of procedure calls without having to declare the size of the stack at assembly time. An example of passing arguments using a stack is shown in Figure 4-17. Register %r14 serves as the stack pointer (%sp) which is

initialized by the operating system prior to execution of the calling routine. The calling routine places its arguments (%r1 and %r2) onto the stack by decrementing the stack pointer (which moves %sp to the next free word above the stack) and by storing each argument on the new top of the stack. Subroutine add_3 is called, which pops its arguments from the stack, performs an addition operation, and then stores its return value on the top of the stack before returning. The calling routine then retrieves its argument from the top of the stack and continues execution.

For each of the calling conventions, the call instruction is used, which saves the current PC in %r15. When a subroutine finishes execution, it needs to return to the instruction that follows the call, which is one word (four bytes) past the saved PC. Thus, the statement “jmpl %r15 + 4, %r0” completes the return. If the called routine calls another routine, however, then the value of the PC that was originally saved in %r15 will be overwritten by the nested call, which means that a correct return to the original calling routine through %r15 will no longer be possible. In order to allow nested calls and returns, the current value of %r15 (which is called the link register) should be saved on the stack, along with any other registers that need to be restored after the return.

If a register based calling convention is used, then the link register should be saved in one of the unused registers before a nested call is made. If a data link area is used, then there should be space reserved within it for the link register. If a stack scheme is used, then the link register should be saved on the stack. For each of the calling conventions, the link register and the local variables in the called routines should be saved before a nested call is made, otherwise, a nested call to the same routine will cause the local variables to be overwritten.

There are many variations to the basic calling conventions, but the stack-oriented approach to subroutine linkage is probably the most popular. When a stack based calling convention is used that handles nested subroutine calls, a stack frame is built that contains arguments that are passed to a called routine, the return address for the calling routine, and any local variables. A sample high level program is shown in Figure 4-18 that illustrates nested function calls. The operation that the program performs is not important, nor is the fact that the C programming language is used, but what is important is how the subroutine calls are implemented.

The behavior of the stack for this program is shown in Figure 4-19. The main program calls func_1 with arguments 1 and 2, and then calls func_2 with argument 10 before finishing execution. Function func_1 has two local vari- ables i and j that are used in computing the return value j. Function func_2 has two local variables m and n that are used in creating the arguments to pass through to func_1 before returning m.

The stack pointer (%r14 by convention, which will be referred to as %sp) is ini- tialized before the program starts executing, usually by the operating system. The compiler is responsible for implementing the calling convention, and so the compiler produces code for pushing parameters and the return address onto the stack, reserving room on the stack for local variables, and then reversing the pro-

cess as routines return from their calls. The stack behavior shown in Figure 4-19 is thus produced as the result of executing compiler generated code, but the code may just as well have been written directly in assembly language.

As the main program begins execution, the stack pointer points to the top element of the system stack (Figure 4-19a). When the main routine calls func_1 at line 03 of the program shown in Figure 4-18 with arguments 1 and 2, the arguments are pushed onto the stack, as shown in Figure 4-19b. Control is then transferred to func_1 through a call instruction (not shown), and func_1 then saves the return address, which is in %r15 as a result of the call instruction, onto the stack (Figure 4-19c). Stack space is reserved for local variables i and j of func_1 (Figure 4-19d). At this point, we have a complete stack frame for the func_1 call as shown in Figure 4-19d, which is composed of the arguments passed to func_1, the return address to the main routine, and the local variables for func_1.

Just prior to func_1 returning to the calling routine, it releases the stack space

for its local variables, retrieves the return address from the stack, releases the stack space for the arguments passed to it, and then pushes its return value onto the stack as shown in Figure 4-19e. Control is then returned to the calling routine through a jmpl instruction, and the calling routine is then responsible for retrieving the returned value from the stack and decrementing the stack pointer to its position from before the call, as shown in Figure 4-19f. Routine func_2 is then executed, and the process of building a stack frame starts all over again as shown in Figure 4-19g. Since func_2 makes a call to func_1 before it returns, there will be stack frames for both func_2 and func_1 on the stack at the same time as shown in Figure 4-19h. The process then unwinds as before, finally resulting in the stack pointer at its original position as shown in Figure 4-19(i-k).

Examples of Assembly Language Programs

The process of writing an assembly language program is similar to the process of writing a high-level program, except that many of the details that are abstracted away in high-level programs are made explicit in assembly language programs. In this section, we take a look at two examples of ARC assembly language programs.

Program: Add Two Integers.

Consider writing an ARC assembly language program that adds the integers 15 and 9. One possible coding is shown in Figure 4-13. The program begins and ends with a .begin/.end pair. The .org pseudo-op instructs the assembler to begin assembling so that the assembled code is loaded into memory starting at location 2048. The operands 15 and 9 are stored in variables x and y, respectively. We can only add numbers that are stored in registers in the ARC (because

only ld and st can access main memory), and so the program begins by loading registers %r1 and %r2 with x and y. The addcc instruction adds %r1 and %r2 and places the result in %r3. The st instruction then stores %r3 in memory location z. The jmpl instruction with operands %r15 + 4, %r0 causes a return to the next instruction in the calling routine, which is the operating sys- tem if this is the highest level of a user’s program as we can assume it is here. The variables x, y, and z follow the program.

In practice, the SPARC code equivalent to the ARC code shown in Figure 4-13 is not entirely correct. The ld, st, and jmpl instructions all take at least two instruction cycles to complete, and since SPARC begins a new instruction at each clock tick, these instructions need to be followed by an instruction that does not rely on their results. This property of launching a new instruction before the previous one has completed is called pipelining, and is covered in more detail in Chapter 9.

Program: Sum an Array of Integers

Now consider a more complex program that sums an array of integers. One pos- sible coding is shown in Figure 4-14. As in the previous example, the program begins and ends with a .begin/.end pair. The .org pseudo-op instructs the assembler to begin assembling so that the assembled code is loaded into memory starting at location 2048. A pseudo-operand is created for the symbol a_start which is assigned a value of 3000.

The program begins by loading the length of array a, which is given in bytes, into %r1. The program then loads the starting address of array a into %r2, and

clears %r3 which will hold the partial sum. Register %r3 is cleared by ANDing it with %r0, which always holds the value 0. Register %r0 can be ANDed with any register for that matter, and the result will still be zero.

The label loop begins a loop that adds successive elements of array a into the partial sum (%r3) on each iteration. The loop starts by checking if the number of remaining array elements to sum (%r1) is zero. It does this by ANDing %r1 with itself, which has the side effect of setting the condition codes. We are interested in the z flag, which will be set to 1 if %r1 = 0. The remaining flags (n, v, and c) are set accordingly. The value of z is tested by making use of the be instruction. If there are no remaining array elements to sum, then the program branches to done which returns to the calling routine (which might be the operating system, if this is the top level of a user program).

If the loop is not exited after the test for %r1 = 0, then %r1 is decremented by the width of a word in bytes (4) by adding -4. The starting address of array a (which is stored in %r2) and the index into a (%r1) are added into %r4, which then points to a new element of a. The element pointed to by %r4 is then loaded into %r5, which is added into the partial sum (%r3). The top of the loop is then revisited as a result of the “ba loop” statement. The variable length is stored after the instructions. The five elements of array a are placed in an area of memory according to the argument to the .org pseudo-op (location 3000).

Notice that there are three instructions for computing the address of the next array element, given the address of the top element in %r2, and the length of the array in bytes in %r1:

This technique of computing the address of a data value as the sum of a base plus an index is so frequently used that the ARC and most other assembly languages have special “addressing modes” to accomplish it. In the case of ARC, the ld instruction address is computed as the sum of two registers or a register plus a 13-bit constant. Recall that register %r0 always contains the value zero, so by specifying %r0 which is being done implicitly in the ld line above, we are wasting an opportunity to have the ld instruction itself perform the address calculation. A single register can hold the operand address, and we can accomplish in two instructions what takes three instructions in the example:

Notice that we also save a register, %r4, which was used as a temporary place holder for the address.

VARIATIONS IN MACHINE ARCHITECTURES AND ADDRESSING

The ARC is typical of a load/store computer. Programs written for load/store machines generally execute faster, in part due to reducing CPU-memory traffic by loading operands into the CPU only once, and storing results only when the computation is complete. The increase in program memory size is usually considered to be a worthwhile price to pay.

Such was not the case when memories were orders of magnitude more expensive and CPUs were orders of magnitude smaller, as was the situation earlier in the computer age. Under those earlier conditions, for CPUs that had perhaps only a single register to hold arithmetic values, intermediate results had to be stored in memory. Machines had three-address, two-address, and one-address arithmetic instructions. By this we mean that an instruction could do arithmetic with 3, 2, or 1 of its operands or results in memory, as opposed to the ARC, where all arithmetic and logic operands must be in registers.

Let us consider how the C expression A = B*C + D might be evaluated by each of the three- two- and one-address instruction types. In the examples below, when referring to a variable “A,” this actually means “the operand whose address is A.” In order to calculate some performance statistics for the program fragments below we will make the following assumptions:

• Addresses and data words are 16-bits – a not uncommon size in earlier ma- chines.

• Opcodes are 8-bits in size.

• Operands and opcodes are moved to and from memory one word at a time. We will compute both program size, in bytes, and program memory traffic with these assumptions.

Memory traffic has two components: the code itself, which must be fetched from memory to the CPU in order to be executed, and the data values—operands must be moved into the CPU in order to be operated upon, and results moved back to memory when the computation is complete. Observing these computations allows us to visualize some of the trade-offs between program size and memory traffic that the various instruction classes offer.

Three-Address Instructions

In a three-address instruction, the expression A = B*C + D might be coded as:

which means multiply B by C and store the result at A. (The mult and add operations are generic; they are not ARC instructions.) Then, add D to A (at this point in the program, A holds the temporary result of multiplying B times C) and store the result at address A. The program size is 7×2 or 14 bytes. Memory traffic is 16 + 2x(2×3) or 28 bytes.

Two Address Instructions

In a two-address instruction, one of the operands is overwritten by the result. Here, the code for the expression A = B*C + D is:

The program size is now 3x3x2) or 18 bytes. Memory traffic is 18 + 2×2 + 2x2x3 or 34 bytes.

One Address, or Accumulator Instructions

A one-address instruction employs a single arithmetic register in the CPU, known as the accumulator. The accumulator typically holds one arithmetic operand, and also serves as the target for the result of an arithmetic operation. The one-address format is not in common use these days, but was more common in the early days of computing when registers were more expensive and frequently served multiple purposes. It serves as temporary storage for one of the operands and also for the result. The code for the expression A = B*C + D is now:

The load instruction loads B into the accumulator, mult multiplies C by the accumulator and stores the result in the accumulator, and add does the corresponding addition. The store instruction stores the accumulator in A. The pro- gram size is now 2´2´4 or 16 bytes, and memory traffic is 16 + 4´2 or 24 bytes.

Special-Purpose Registers

In addition to the general-purpose registers and the accumulator described above, most modern architectures include other registers that are dedicated to specific purposes. Examples include

• Memory index registers: The Intel 80×86 Source Index (SI) and Destination Index (DI) registers. These are used to point to the beginning or end of an array in memory. Special “string” instructions transfer a byte or a word from the starting memory location pointed to by SI to the ending memory location pointed to by DI, and then increment or decrement these registers to point to the next byte or word.

• Floating point registers: Many current-generation processors have special registers and instructions that handle floating point numbers.

• Registers to support time, and timing operations: The PowerPC 601 processor has Real-Time Clock registers that provide a high-resolution mea- sure of real time for indicating the date and the time of day. They provide a range of approximately 135 years, with a resolution of 128 ns.

• Registers in support of the operating system: most modern processors have registers to support the memory system.

• Registers that can be accessed only by “privileged instructions,” or when in “Supervisor mode.” In order to prevent accidental or malicious damage to the system, many processors have special instructions and registers that are unavailable to the ordinary user and application program. These instructions and registers are used only by the operating system.

PERFORMANCE OF INSTRUCTION SET ARCHITECTURES

While the program size and memory usage statistics calculated above are observed out of context from the larger programs in which they would be contained, they do show that having even one temporary storage register in the CPU can have a significant effect on program performance. In fact, the Intel Pentium processor, considered among the faster of the general-purpose CPUs, has only a single accumulator, though it has a number of special-purpose registers that sup- port it. There are many other factors that affect real-world performance of an instruction set, such as the time an instruction takes to perform its function, and the speed at which the processor can run.

Pseudo- Ops

In addition to the ARC instructions that are supported by the architecture, there are also pseudo-operations (pseudo-ops) that are not opcodes at all, but rather instructions to the assembler to perform some action at assembly time. A list of pseudo-ops and examples of their usages are shown in Figure 4-12. Note that

unlike processor opcodes, which are specific to a given machine, the kind and nature of the pseudo-ops are specific to a given assembler, because they are executed by the assembler itself.

The .equ pseudo-op instructs the assembler to equate a value or a character string with a symbol, so that the symbol can be used throughout a program as if the value or string is written in its place. The .begin and .end pseudo-ops tell the assembler when to start and stop assembling. Any statements that appear before .begin or after .end are ignored. A single program may have more than one .begin/.end pair, but there must be a .end for every .begin, and there must be at least one .begin. The use of .begin and .end are helpful in making portions of the program invisible to the assembler during debugging.

The .org (origin) pseudo-op causes the next instruction to be assembled with the assumption it will be placed in the specified memory location at runtime (location 2048 in Figure 4-12.) The .dwb (define word block) pseudo-op reserves a block of four-byte words, typically for an array. The location counter (which keeps track of which instruction is being assembled by the assembler) is moved ahead of the block according to the number of words specified by the argument to .dwb multiplied by 4.

The .global and .extern pseudo-ops deal with names of variables and addresses that are defined in one assembly code module and are used in another. The .global pseudo-op makes a label available for use in other modules. The

.extern pseudo-op identifies a label that is used in the local module and is defined in another module (which should be marked with a .global in that module). We will see how .global and .extern are used when linking and loading are covered in the next chapter. The .macro, .endmacro, .if, and .endif pseudo-ops are also covered in the next chapter.

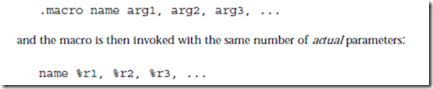
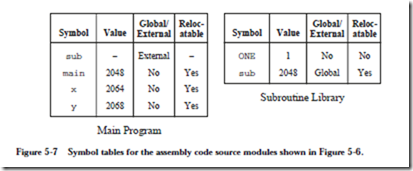
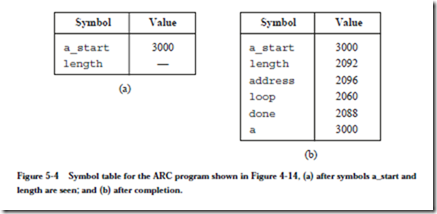
ARC, A RISC Computer

In the remainder of this chapter, we will study a model architecture that is based on the commercial Scalable Processor Architecture (SPARC) processor that was developed at Sun Microsystems in the mid-1980’s. The SPARC has become a

popular architecture since its introduction, which is partly due to its “open” nature: the full definition of the SPARC architecture is made readily available to the public (SPARC, 1992). In this chapter, we will look at just a subset of the SPARC, which we call “A RISC Computer” (ARC). “RISC” is yet another acronym, for reduced instruction set computer, which is discussed in Chapter 9. The ARC has most of the important features of the SPARC architecture, but without some of the more complex features that are present in a commercial processor.

ARC MEMORY

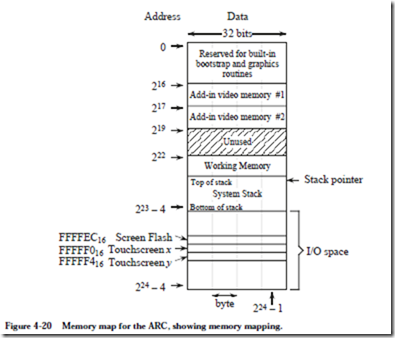
The ARC is a 32-bit machine with byte-addressable memory: it can manipulate 32-bit data types, but all data is stored in memory as bytes, and the address of a 32-bit word is the address of its byte that has the lowest address. As described earlier in the chapter in the context of Figure 4-4, the ARC has a 32-bit address space, in which our example architecture is divided into distinct regions for use by the operating system code, user program code, the system stack (used to store temporary data), and input and output, (I/O). These memory regions are detailed as follows:

• The lowest 211 = 2048 addresses of the memory map are reserved for use by the operating system.

• The user space is where a user’s assembled program is loaded, and can grow during operation from location 2048 until it meets up with the system stack.

• The system stack starts at location 231 – 4 and grows toward lower addresses. The reason for this organization of programs growing upward in memory and the system stack growing downward can be seen in Figure 4-4: it accommodates both large programs with small stacks and small programs with large stacks.

• The portion of the address space between 231 and 232 – 1 is reserved for I/O devices—each device has a collection of memory addresses where its data is stored, which is referred to as “memory mapped I/O.”

The ARC has several data types (byte, halfword, integer, etc.), but for now we will consider only the 32-bit integer data type. Each integer is stored in memory as a collection of four bytes. ARC is a big-endian architecture, so the highest-order byte is stored at the lowest address. The largest possible byte address in the ARC is 232 – 1, so the address of the highest word in the memory map is three bytes lower than this, or 2³² – 4.

ARC INSTRUCTION SET

As we get into details of the ARC instruction set, let us start by making an over- view of the CPU:

• The ARC has 32 32-bit general-purpose registers, as well as a PC and an IR.

• There is a Processor Status Register (PSR) that contains information about the state of the processor, including information about the results of arithmetic operations. The “arithmetic flags” in the PSR are called the condition codes. They specify whether a specified arithmetic operation resulted in a zero value (z), a negative value (n), a carry out from the 32-bit ALU (c), and an overflow (v). The v bit is set when the results of the arithmetic operation are too large to be handled by the ALU.

• All instructions are one word (32-bits) in size.

• The ARC is a load–store machine: the only allowable memory access operations load a value into one of the registers, or store a value contained in one of the registers into a memory location. All arithmetic operations operate on values that are contained in registers, and the results are placed in a register. There are approximately 200 instructions in the SPARC instruction set, upon which the ARC instruction set is based. A subset of 15 instructions is shown in Figure 4-7. Each instruction is represented by a mnemonic, which is a name that represents the instruction.

Data Movement Instructions

The first two instructions: ld (load) and st (store) transfer a word between the main memory and one of the ARC registers. These are the only instructions that can access memory in the ARC.

The sethi instruction sets the 22 most significant bits (MSBs) of a register with a 22-bit constant contained within the instruction. It is commonly used for constructing an arbitrary 32-bit constant in a register, in conjunction with another instruction that sets the low-order 10 bits of the register.

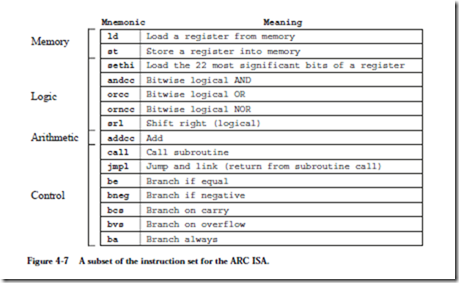
Arithmetic and Logic Instructions

The andcc, orcc, and orncc instructions perform a bit-by-bit AND, OR, and NOR operation, respectively, on their operands. One of the two source operands must be in a register. The other may either be in a register, or it may be a 13-bit two’s complement constant contained in the instruction, which is sign extended to 32-bits when it is used. The result is stored in a register.

For the andcc instruction, each bit of the result is set to 1 if the corresponding bits of both operands are 1, otherwise the result bit is set to 0. For the orcc instruction, each bit of the register is 1 if either or both of the corresponding source operand bits are 1, otherwise the corresponding result bit is set to 0. The orncc operation is the complement of orcc, so each bit of the result is 0 if either or both of the corresponding operand bits are 1, otherwise the result bit is set to 1. The “cc” suffixes specify that after performing the operation, the condition code bits in the PSR are updated to reflect the results of the operation. In particular, the z bit is set if the result register contains all zeros, the n bit is set if the most significant bit of the result register is a 1, and the c and v flags are cleared for these particular instructions. (Why?)

The shift instructions shift the contents of one register into another. The srl (shift right logical) instruction shifts a register to the right, and copies zeros into the leftmost bit(s). The sra (shift right arithmetic) instruction (not shown), shifts the original register contents to the right, placing a copy of the MSB of the original register into the newly created vacant bit(s) in the left side of the register. This results in sign-extending the number, thus preserving its arithmetic sign.

The addcc instruction performs a 32-bit two’s complement addition on its operands.

Control Instructions

The call and jmpl instructions form a pair that are used in calling and return- ing from a subroutine, respectively. jmpl is also used to transfer control to another part of the program.

The lower five instructions are called conditional branch instructions. The be, bneg, bcs, bvs, and ba instructions cause a branch in the execution of a pro- gram. They are called conditional because they test one or more of the condition code bits in the PSR, and branch if the bits indicate the condition is met. They are used in implementing high level constructs such as goto, if-then-else and do-while. Detailed descriptions of these instructions and examples of their usages are given in the sections that follow.

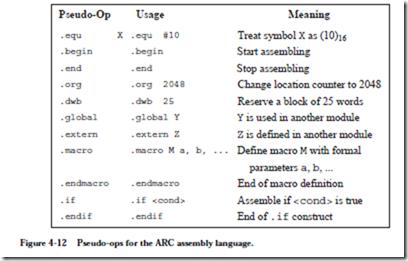
4.2.3 ARC ASSEMBLY LANGUAGE FORMAT

Each assembly language has its own syntax. We will follow the SPARC assembly language syntax, as shown in Figure 4-8. The format consists of four fields: an

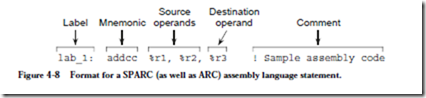
optional label field, an opcode field, one or more fields specifying the source and destination operands (if there are operands), and an optional comment field. A label consists of any combination of alphabetic or numeric characters, under- scores (_), dollar signs ($), or periods (.), as long as the first character is not a digit. A label must be followed by a colon. The language is sensitive to case, and so a distinction is made between upper and lower case letters. The language is “free format” in the sense that any field can begin in any column, but the relative left-to-right ordering must be maintained.

The ARC architecture contains 32 registers labeled %r0 – %r31, that each hold a 32-bit word. There is also a 32-bit Processor State Register (PSR) that describes the current state of the processor, and a 32-bit program counter (PC), that keeps track of the instruction being executed, as illustrated in Figure 4-9. The

PSR is labeled %psr and the PC register is labeled %pc. Register %r0 always contains the value 0, which cannot be changed. Registers %r14 and %r15 have additional uses as a stack pointer (%sp) and a link register, respectively, as described later.

Operands in an assembly language statement are separated by commas, and the destination operand always appears in the rightmost position in the operand field. Thus, the example shown in Figure 4-8 specifies adding registers %r1 and %r2, with the result placed in %r3. If %r0 appears in the destination operand field instead of %r3, the result is discarded. The default base for a numeric operand is 10, so the assembly language statement:

addcc %r1, 12, %r3

shows an operand of (12)10 that will be added to %r1, with the result placed in %r3. Numbers are interpreted in base 10 unless preceded by “0x” or ending in “H”, either of which denotes a hexadecimal number. The comment field follows the operand field, and begins with an exclamation mark ‘!’ and terminates at the end of the line.

ARC INSTRUCTION FORMATS

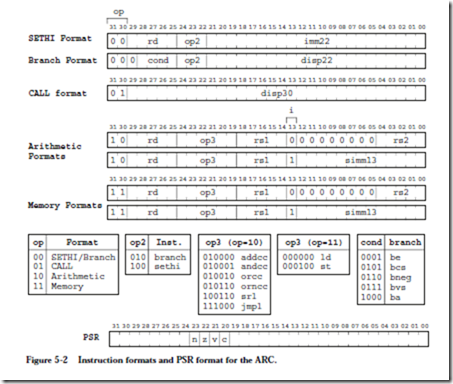
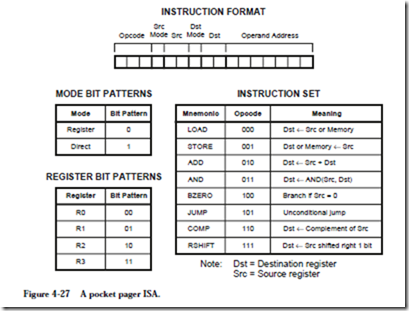
The instruction format defines how the various bit fields of an instruction are laid out by the assembler, and how they are interpreted by the ARC control unit. The ARC architecture has just a few instruction formats. The five formats are: SETHI, Branch, Call, Arithmetic, and Memory, as shown in Figure 4-10. Each

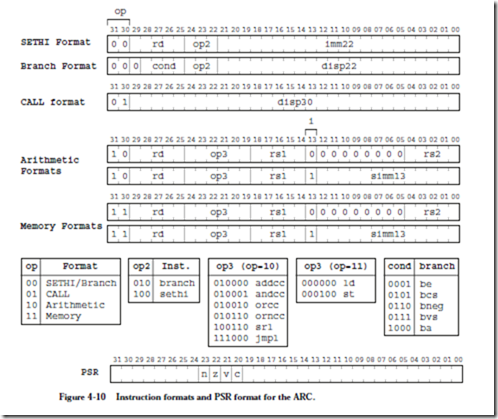
instruction has a mnemonic form such as “ld,” and an opcode. A particular instruction format may have more than one opcode field, which collectively identify an instruction in one of its various forms. (Note that these four instruction formats do not directly correspond to the four instruction classifications shown in Figure 4-7.)

The leftmost two bits of each instruction form the op (opcode) field, which identifies the format. The SETHI and Branch formats both contain 00 in the op field, and so they can be considered together as the SETHI/Branch format. The actual SETHI or Branch format is determined by the bit pattern in the op2 opcode field (010 = Branch; 100 = SETHI). Bit 29 in the Branch format always contains a zero. The five-bit rd field identifies the target register for the SETHI operation.

The cond field identifies the type of branch, based on the condition code bits (n, z, v, and c) in the PSR, as indicated at the bottom of Figure 4-10. The result of executing an instruction in which the mnemonic ends with “cc” sets the condition code bits such that n=1 if the result of the operation is negative; z=1 if the result is zero; v=1 if the operation causes an overflow; and c=1 if the operation produces a carry. The instructions that do not end in “cc” do not affect the condition codes. The imm22 and disp22 fields each hold a 22-bit constant that is used as the operand for the SETHI format (for imm22) or for calculating a dis- placement for a branch address (for disp22).

The CALL format contains only two fields: the op field, which contains the bit pattern 01, and the disp30 field, which contains a 30-bit displacement that is used in calculating the address of the called routine.

The Arithmetic (op = 10) and Memory (op = 11) formats both make use of rd fields to identify either a source register for st, or a destination register for the remaining instructions. The rs1 field identifies the first source register, and the rs2 field identifies the second source register. The op3 opcode field identifies the instruction according to the op3 tables shown in Figure 4-10.

The simm13 field is a 13-bit immediate value that is sign extended to 32 bits for the second source when the i (immediate) field is 1. The meaning of “sign extended” is that the leftmost bit of the simm13 field (the sign bit) is copied to the left into the remaining bits that make up a 32-bit integer, before adding it to rs1 in this case. This ensures that a two’s complement negative number remains negative (and a two’s complement positive number remains positive). For instance, (-13)10 = (1111111110011)2, and after sign extension to a 32-bit integer, we have (11111111111111111111111111110011)2 which is still equivalent to (-13)10.

The Arithmetic instructions need two source operands and a destination operand, for a total of three operands. The Memory instructions only need two operands: one for the address and one for the data. The remaining source operand is also used for the address, however. The operands in the rs1 and rs2 fields are added to obtain the address when i = 0. When i = 1, then the rs1 field and the simm13 field are added to obtain the address. For the first few examples we will encounter, %r0 will be used for rs2 and so only the remaining source operand will be specified.

ARC DATA FORMATS

The ARC supports 12 different data formats as illustrated in Figure 4-11. The data formats are grouped into three types: signed integer, unsigned integer, and floating point. Within these types, allowable format widths are byte (8 bits), half- word (16 bits), word/singleword (32 bits), tagged word (32 bits, in which the two least significant bits form a tag and the most significant 30 bits form the value), doubleword (64 bits), and quadword (128 bits).

In reality, the ARC does not differentiate between unsigned and signed integers. Both are stored and manipulated as two’s complement integers. It is their interpretation that varies. In particular one subset of the branch instructions assumes that the value(s) being compared are signed integers, while the other subset assumes they are unsigned. Likewise, the c bit indicates unsigned integer over- flow, and the v bit, signed overflow.

The tagged word uses the two least significant bits to indicate overflow, in which an attempt is made to store a value that is larger than 30 bits into the allocated 30 bits of the 32-bit word. Tagged arithmetic operations are used in languages with dynamically typed data, such as Lisp and Smalltalk. In its generic form, a 1 in either bit of the tag field indicates an overflow situation for that word. The tags can be used to ensure proper alignment conditions (that words begin on four-byte boundaries, quadwords begin on eight-byte boundaries, etc.), particularly for pointers.

The floating point formats conform to the IEEE 754-1985 standard (see Chapter 2). There are special instructions that invoke the floating point formats that are not described here, that can be found in (SPARC, 1992).

4.2.6 ARC INSTRUCTION DESCRIPTIONS

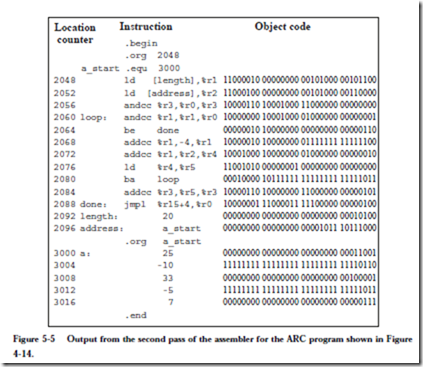
Now that we know the instruction formats, we can create detailed descriptions of the 15 instructions listed in Figure 4-7, which are given below. The translation to object code is provided only as a reference, and is described in detail in the next chapter. In the descriptions below, a reference to the contents of a memory location (for ld and st) is indicated by square brackets, as in “ld [x], %r1” which copies the contents of location x into %r1. A reference to the address of a

memory location is specified directly, without brackets, as in “call sub_r,” which makes a call to subroutine sub_r. Only ld and st can access memory, therefore only ld and st use brackets. Registers are always referred to in terms of their contents, and never in terms of an address, and so there is no need to enclose references to registers in brackets.

Instruction: ld

Description: Load a register from main memory. The memory address must be aligned on a word boundary (that is, the address must be evenly divisible by 4). The address is computed by adding the contents of the register in the rs1 field to either the contents of the register in the rs2 field or the value in the simm13 field, as appropriate for the con- text.

Description: Store a register into main memory. The memory address must be aligned on a word boundary. The address is computed by adding the contents of the register in the rs1 field to either the contents of the register in the rs2 field or the value in the simm13 field, as appropriate for the context. The rd field of this instruction is actually used for the source register.

Instruction: sethi

Description: Set the high 22 bits and zero the low 10 bits of a register. If the operand is 0 and the register is %r0, then the instruction behaves as a no-op (NOP), which means that no operation takes place.

Example usage: sethi 0x304F15, %r1

Meaning: Set the high 22 bits of %r1 to (304F15)16, and set the low 10 bits to zero.

Object code: 00000011001100000100111100010101

Instruction: andcc

Description: Bitwise AND the source operands into the destination operand. The condition codes are set according to the result.

Example usage: andcc %r1, %r2, %r3

Meaning: Logically AND %r1 and %r2 and place the result in %r3.

Object code: 10000110100010000100000000000010

Instruction: orcc

Description: Bitwise OR the source operands into the destination operand. The condition codes are set according to the result.

Example usage: orcc %r1, 1, %r1

Meaning: Set the least significant bit of %r1 to 1.

Object code: 10000010100100000110000000000001

Instruction: orncc

Description: Bitwise NOR the source operands into the destination operand. The con- dition codes are set according to the result.

Example usage: orncc %r1, %r0, %r1

Meaning: Complement %r1.

Object code: 10000010101100000100000000000000

Instruction: srl

Description: Shift a register to the right by 0 – 31 bits. The vacant bit positions in the left side of the shifted register are filled with 0’s.

Example usage: srl %r1, 3, %r2

Meaning: Shift %r1 right by three bits and store in %r2. Zeros are copied into the three most significant bits of %r2.

Object code: 10000101001100000110000000000011

Instruction: addcc

Description: Add the source operands into the destination operand using two’s complement arithmetic. The condition codes are set according to the result.

Example usage: addcc %r1, 5, %r1

Meaning: Add 5 to %r1.

Object code: 10000010100000000110000000000101

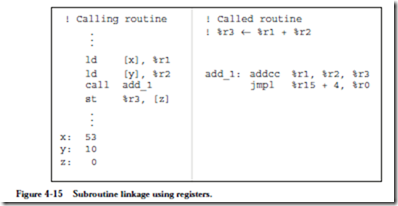
Instruction: call

Description: Call a subroutine and store the address of the current instruction (where the call itself is stored) in %r15, which effects a “call and link” operation. In the assem- bled code, the disp30 field in the CALL format will contain a 30-bit displacement from the address of the call instruction. The address of the next instruction to be exe- cuted is computed by adding 4 ´ disp30 (which shifts disp30 to the high 30 bits of the 32-bit address) to the address of the current instruction. Note that disp30 can be negative.

Example usage: call sub_r

Meaning: Call a subroutine that begins at location sub_r. For the object code shown below, sub_r is 25 words (100 bytes) farther in memory than the call instruction. Object code: 01000000000000000000000000011001

Instruction: jmpl

Description: Jump and link (return from subroutine). Jump to a new address and store the address of the current instruction (where the jmpl instruction is located) in the destination register.

Example usage: jmpl %r15 + 4, %r0

Meaning: Return from subroutine. The value of the PC for the call instruction was previously saved in %r15, and so the return address should be computed for the instruction that follows the call, at %r15 + 4. The current address is discarded in %r0.

Object code: 10000001110000111110000000000100

Instruction: be

Description: If the z condition code is 1, then branch to the address computed by adding 4 ´ disp22 in the Branch instruction format to the address of the current instruction. If the z condition code is 0, then control is transferred to the instruction that follows be.

Example usage: be label

Meaning: Branch to label if the z condition code is 1. For the object code shown below, label is five words (20 bytes) farther in memory than the be instruction. Object code: 00000010100000000000000000000101

Instruction: bneg

Description: If the n condition code is 1, then branch to the address computed by add- ing 4 ´ disp22 in the Branch instruction format to the address of the current instruction. If the n condition code is 0, then control is transferred to the instruction that follows bneg.

Example usage: bneg label

Meaning: Branch to label if the n condition code is 1. For the object code shown below, label is five words farther in memory than the bneg instruction.

Object code: 00001100100000000000000000000101

Instruction: bcs

Description: If the c condition code is 1, then branch to the address computed by adding 4 ´ disp22 in the Branch instruction format to the address of the current instruction. If the c condition code is 0, then control is transferred to the instruction that follows bcs.

Example usage: bcs label

Meaning: Branch to label if the c condition code is 1. For the object code shown below, label is five words farther in memory than the bcs instruction.

Object code: 00001010100000000000000000000101

Instruction: bvs

Description: If the v condition code is 1, then branch to the address computed by adding 4 ´ disp22 in the Branch instruction format to the address of the current instruction. If the v condition code is 0, then control is transferred to the instruction that follows bvs.

Example usage: bvs label

Meaning: Branch to label if the v condition code is 1. For the object code shown below, label is five words farther in memory than the bvs instruction.

Object code: 00001110100000000000000000000101

Instruction: ba

Description: Branch to the address computed by adding 4 ´ disp22 in the Branch instruction format to the address of the current instruction.

Example usage: ba label

Meaning: Branch to label regardless of the settings of the condition codes. For the object code shown below, label is five words earlier in memory than the ba instruction.

Object code: 00010000101111111111111111111011