THE z-TRANSFORM
Equation (6.7) defines an infinite series with powers of e−snT . The z-transform is defined so that
i.e. the r (nT ) are the coefficients of this power series at different sampling instants.
The z-transformation is used in sampled data systems just as the Laplace transformation is used in continuous-time systems. The response of a sampled data system can be determined easily by finding the z-transform of the output and then calculating the inverse z-transform,
Tables of z-Transforms
A table of z-transforms for the commonly used functions is given in Table 6.1 (a bigger table is given in Appendix A). As with the Laplace transforms, we are interested in the output response y(t ) ofa system and we must find the inverse z-transform to obtain y(t ) from Y (z).
The z-Transform of a Function Expressed as a Laplace Transform It is important to realize that although we denote the z-transform equivalent of G(s) by G(z), G(z) is not obtained by simply substituting z for s in G(s). We can use one of the following methods to find the z-transform of a function expressed in Laplace transform format:
• Given G(s), calculate the time response g(t ) by finding the inverse Laplace transform of G(s).
Then find the z-transform either from the first principles, or by looking at the z-transform tables.
• Given G(s), find the z-tranform G(z) by looking at the tables which give the Laplace trans- forms and their equivalent z-transforms (e.g. Table 6.1).
• Given the Laplace transform G(s), express it in the form G(s) = N (s)/D(s) and then use the following formula to find the z-transform G(z):
Method 2: By using the z-transform transform tables for the partial product. From Table 6.1, the z-transform of 1/(s + a) is z/(z − e−aT ). Therefore the z-transform of (6.16) is
The inverse z-transform is obtained in a similar way to the inverse Laplace transforms. Gener- ally, the z-transforms are the ratios of polynomials in the complex variable z, with the numerator polynomial being of order no higher than the denominator. By finding the inverse z-transform we find the sequence associated with the given z-transform polynomial. As in the case of inverse Laplace transforms, we are interested in the output time response of a system. There- fore, we use an inverse transform to obtain y(t ) from Y (z). There are several methods to find the inverse z-transform of a given function. The following methods will be described here:
• power series (long division);
• expanding Y (z) into partial fractions and using z-transform tables to find the inverse transforms;
• obtaining the inverse z-transform using an inversion integral.
Given a z-transform function Y (z), we can find the coefficients of the associated sequence y(nT )at the sampling instants by using the inverse z-transform. The time function y(t ) is then determined as
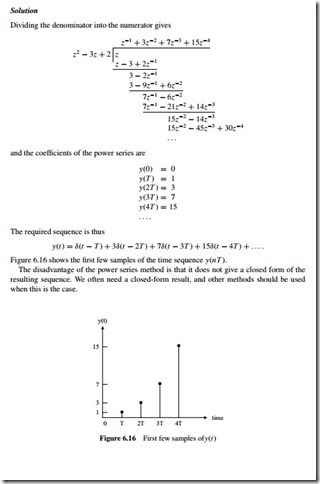
Solution
Dividing the denominator into the numerator gives
Method 2: Partial fractions. Similar to the inverse Laplace transform techniques, a partial fraction expansion of the function Y (z) can be found, and then tables of known z-transforms can be used to determine the inverse z-transform. Looking at the z-transform tables, we see that there is usually a z term in the numerator. It is therefore more convenient to find the partial fractions of the function Y (z)/z and then multiply the partial fractions by z to obtain a z term in the numerator.
The process of finding inverse z-transforms is aided by considering what form is taken by the roots of Y (z). It is useful to distinguish the case of distinct real roots and that of multiple order roots.