PULSE TRANSFER FUNCTION AND MANIPULATION OF BLOCK DIAGRAMS
The pulse transfer function is the ratio of the z-transform of the sampled output and the input at the sampling instants.
Suppose we wish to sample a system with output response given by
Equations (6.34) and (6.35) tell us that if at least one of the continuous functions has been sampled, then the z-transform of the product is equal to the product of the z-transforms of each function (note that [e*(s)]* = [e*(s)], since sampling an already sampled signal has no further effect). G(z) is the transfer function between the sampled input and the output at the sampling instants and is called the pulse transfer function. Notice from (6.35) that we have no information about the output y(z) between the sampling instants.
Open-Loop Systems
Some examples of manipulating open-loop block diagrams are given in this section.
Example 6.15
Figure 6.18 shows an open-loop sampled data system. Derive an expression for the z-transform of the output of the system.
Open-Loop Time Response
The open-loop time response of a sampled data system can be obtained by finding the inverse z-transform of the output function. Some examples are given below.
Example 6.18
A unit step signal is applied to the electrical RC system shown in Figure 6.21. Calculate and draw the output response of the system, assuming a sampling period of T = 1 s.
Solution
The transfer function of the RC system is
It is important to notice that the response is only known at the sampling instants. For example, in Figure 6.22 the capacitor discharges through the resistor between the sampling instants, and this causes an exponential decay in the response between the sampling intervals. But this behaviour between the sampling instants cannot be determined by the z-transform method of analysis.
Example 6.19
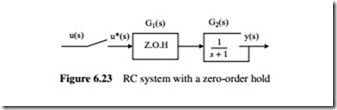
Assume that the system in Example 6.17 is used with a zero-order hold (see Figure 6.23). What will the system output response be if (i) a unit step input is applied, and (ii) if a unit ramp input is applied.
Example 6.20
The open-loop block diagram of a system with a zero-order hold is shown in Figure 6.26. Calculate and plot the system response when a step input is applied to the system, assuming that T = 1 s.