THE ARITHMETIC COPROCESSOR, MMX, AND SIMD TECHNOLOGIES
INTRODUCTION
The Intel family of arithmetic coprocessors includes the 8087, 80287, 80387SX, 80387DX, and the 80487SX for use with the 80486SX microprocessor. The 80486DX–Core2 microprocessors contain their own built-in arithmetic coprocessors. Be aware that some of the cloned 80486 microprocessors (from IBM and Cyrix) did not contain arithmetic coprocessors. The instruction sets and programming for all devices are almost identical; the main difference is that each coprocessor is designed to function with a different Intel microprocessor. This chapter provides detail on the entire family of arithmetic coprocessors. Because the coprocessor is a part of the 80486DX–Core2, and because these microprocessors are commonplace, many programs now require or at least benefit from a coprocessor.
The family of coprocessors, which is labeled the 80X87, is able to multiply, divide, add, subtract, find the square root, and calculate the partial tangent, partial arctangent, and logarithms. Data types include 16-, 32-, and 64-bit signed integers; l8-digit BCD data; and 32-, 64-, and 80-bit floating-point numbers. The operations performed by the 80X87 generally execute many times faster than equivalent operations written with the most efficient programs that use the microprocessor’s normal instruction set. With the improved Pentium coprocessor, operations execute about five times faster than those performed by the 80486 microprocessor with an equal clock frequency. Note that the Pentium can often execute a coprocessor instruction and two integer instructions simultaneously. The Pentium Pro through Core2 coprocessors are similar in performance to the Pentium coprocessor, except that a few new instructions have been added: FCMOV and FCOMI.
The multimedia extensions (MMX) to the Pentium–Core2 are instructions that share the arithmetic coprocessor register set. The MMX extension is a special internal processor designed to execute integer instructions at high-speed for external multimedia devices. For this reason, the MMX instruction set and specifications have been placed in this chapter. The SIMD (single- instruction, multiple data) extensions, which are called SSE (streaming SIMD extensions), are similar to the MMX instructions, but function with floating-point numbers instead of integers and do not use the coprocessor register space as do MMX instructions.
CHAPTER OBJECTIVES
Upon completion of this chapter, you will be able to:
1. Convert between decimal data and signed integer, BCD, and floating-point data for use by the arithmetic coprocessor, MMX, and SIMD technologies.
2. Explain the operation of the 80X87 arithmetic coprocessor and the MMX and SIMD units.
3. Explain the operation and addressing modes of each arithmetic coprocessor, MMX, and SSE instruction.
4. Develop programs that solve complex arithmetic problems using the arithmetic coprocessor, MMX, and SIMD instructions.
DATA FORMATS FOR THE ARITHMETIC COPROCESSOR
This section of the text presents the types of data used with all arithmetic coprocessor family members. (See Table 14–1 for a listing of all Intel microprocessors and their companion coprocessors.) These data types include signed integer, BCD, and floating-point. Each has a specific use in a system, and many systems require all three data types. Note that assembly language programming with the coprocessor is often limited to modifying the coding generated by a high- level language such as C/C++. In order to accomplish any such modification, the instruction set and some basic programming concepts are required, which are presented in this chapter.
Signed Integers
The signed integers used with the coprocessor are the same as those described in Chapter 1. When used with the arithmetic coprocessor, signed integers are 16- (word), 32- (doubleword integer), or 64-bits (quadword integer) wide. The long integer is new to the coprocessor and is not described in Chapter 1, but the principles are the same. Conversion between decimal and signed integer format is handled in exactly the same manner as for the signed integers described in Chapter 1. As you will recall, positive numbers are stored in true form with a leftmost sign-bit of 0, and negative numbers are stored in two’s complement form with a leftmost sign-bit of 1.
The word integers range in value from -32,768 to +32,767, the doubleword integer range is ±2 ×109, and the quadword integer range is ±9 × 1018. Integer data types are found in some applications that use the arithmetic coprocessor. See Figure 14–1, which shows these three forms of signed integer data.
Data are stored in memory using the same assembler directives described and used in earlier chapters. The DW directive defines words, DD defines doubleword integers, and DQ defines quadword integers. Example 14–1 shows how several different sizes of signed integers are defined for use by the assembler and arithmetic coprocessor.
Binary-Coded Decimal (BCD)
The binary-coded decimal (BCD) form requires 80 bits of memory. Each number is stored as an 18-digit packed integer in nine bytes of memory as two digits per byte. The tenth byte contains only a sign-bit for the 18-digit signed BCD number. Figure 14–2 shows the format of the BCD number used with the arithmetic coprocessor. Note that both positive and negative numbers are stored in true form and never in ten’s complement form. The DT directive stores BCD data in the memory as illustrated in Example 14–2. This form is rarely used because it is unique to the Intel coprocessor.
Floating-point numbers are often called real numbers because they hold signed integers, fractions, and mixed numbers. A floating-point number has three parts: a sign-bit, a biased exponent, and a significand. Floating-point numbers are written in scientific binary notation. The Intel family of arithmetic coprocessors supports three types of floating-point numbers: single (32 bits), double (64 bits), and temporary (80 bits). See Figure 14–3 for the three forms of the floating-point number. Please note that the single form is also called a single-precision number and the double form is called a double-precision number. Sometimes the 80-bit temporary form is called an extended-precision number. The floating-point numbers and the operations performed by the arithmetic coprocessor conform to the IEEE-754 standard, as adopted by all major personal computer software producers. This includes Microsoft, which in 1995 stopped supporting the Microsoft floating-point format and also the ANSI floating-point standard that is popular in some mainframe computer systems.
In Visual C++ 2008 or the Express edition, float, double, and decimal are used for the three data types. The float is a 32-bit version, double is the 64-bit version, and decimal is a special version developed for Visual studio that develops a very accurate floating-point number for use in banking transactions or anything else that requires a high degree of precision. The decimal variable form is new to Visual Studio 2005 and 2008.
Converting to Floating-Point Form. Converting from decimal to the floating-point form is a simple task that is accomplished through the following steps:
1. Convert the decimal number to binary.
2. Normalize the binary number.
3. Calculate the biased exponent.
4. Store the number in the floating-point format.
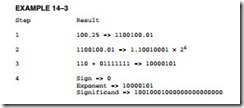
These four steps are illustrated for the decimal number 100.2510 in Example 14–3. Here, the decimal number is converted to a single-precision (32-bit) floating-point number.
In step 3 of Example 14–3, the biased exponent is the exponent, a 26 or 110, plus a bias of 01111111 (7FH) or 10000101 (85H). All single-precision numbers use a bias of 7FH, double- precision numbers use a bias of 3FFH, and extended-precision numbers use a bias of 3FFFH.
In step 4 of Example 14–3, the information found in the prior steps is combined to form the floating-point number. The leftmost bit is the sign-bit of the number. In this case, it is a 0 because the number is +100.2510. The biased exponent follows the sign-bit. The significand is a 23-bit number with an implied one-bit. Note that the significand of a number l.XXXX is the XXXX portion. The 1. is an implied one-bit that is only stored in the extended temporary-precision form of the floating-point number as an explicit one-bit.
Some special rules apply to a few numbers. The number 0, for example, is stored as all zeros except for the sign-bit, which can be a logic 1 to represent a negative zero. The plus and minus infinity is stored as logic 1s in the exponent with a significand of all zeros and the sign-bit that represents plus or minus. A NAN (not-a-number) is an invalid floating-point result that has all ones in the exponent with a significand that is not all zeros.
Converting from Floating-Point Form. Conversion to a decimal number from a floating-point number is summarized in the following steps:
1. Separate the sign-bit, biased exponent, and significand.
2. Convert the biased exponent into a true exponent by subtracting the bias.
3. Write the number as a normalized binary number.
4. Convert it to a denormalized binary number.
5. Convert the denormalized binary number to decimal.
These five steps convert a single-precision floating-point number to decimal, as shown in Example 14–4. Notice how the sign-bit of 1 makes the decimal result negative. Also notice that the implied one-bit is added to the normalized binary result in step 3.
Storing Floating-Point Data in Memory. Floating-point numbers are stored with the assembler using the DD directive for single-precision, DQ for double-precision, and DT for extended temporary-precision. Some examples of floating-point data storage are shown in Example 14–5. The author discovered that the Microsoft macro assembler contains an error that does not allow a plus sign to be used with positive floating-point numbers. A +92.45 must be defined as 92.45 for the assembler to function correctly. Microsoft has assured the author that this error has been corrected in version 6.11 of MASM if the REAL4, REAL8, or REAL10 directives are used in place of DD, DQ, and DT to specify floating-point data. The assembler provides access 8087 emulator if your system does not contain a microprocessor with a coprocessor. The emulator comes with all Microsoft high-level languages or as shareware programs such as EM87. Access the emulator by including the OPTION EMULATOR statement immediately following the .MODEL statement in a program. Be aware that the emulator does not emulate some of the coprocessor instructions. Do not use this option if your system contains a coprocessor. In all cases, you must include the .8087, .80187, .80287, .80387, .80487, .80587, or .80687 switch to enable the generation of coprocessor instructions.