PROGRAMMING WITH THE ARITHMETIC COPROCESSOR
This section of the chapter provides programming examples for the arithmetic coprocessor. Each example is chosen to illustrate a programming technique for the coprocessor.
Calculating the Area of a Circle
This first programming example illustrates a simple method of addressing the coprocessor stack. First, recall that the equation for calculating the area of a circle is A = πR2. A program that per- forms this calculation is listed in Example 14–8. Note that this program takes test data from array RAD that contains five sample radii. The five areas are stored in a second array called AREA. No attempt is made in this program to use the data from the AREA array.
The first instruction loads π to the top of the stack. Next, the contents of memory location RAD [ECX*4], one of the elements of the array, is loaded to the top of the stack. This pushes π to ST(1). Next, the FMUL ST,ST(0) instruction squares the radius on the top of the stack. The FMUL ST,ST(1) instruction forms the area. Finally, the top of the stack is stored in the AREA array and also pops it from the stack in preparation for the next iteration.
Notice how care is taken to always remove all stack data. The last instruction before the RET pops π from the stack. This is important because if data remain on the stack at the end of the procedure, the stack top will no longer be register 0. This could cause problems because software assumes that the top of the stack is register 0. Another way of ensuring that the coprocessor is initialized is to place the FINIT (initialization) instruction at the start of the program.
Finding the Resonant Frequency
An equation commonly used in electronics is the formula for determining the resonant frequency of an LC circuit. The equation solved by the program illustrated in Example 14–9 is
This example uses L1 for the inductance L, C1 for the capacitor C, and RES for the resultant res- onant frequency.
Notice the straightforward manner in which the program solves this equation. Very little extra data manipulation is required because of the stack inside the coprocessor. Notice how FDIVR, using classic stack addressing, is used to form the reciprocal. If you own a reverse Polish notation calculator, such as those produced by Hewlett-Packard, you are familiar with stack addressing. If not, using the coprocessor will increase your experience with this type of entry.
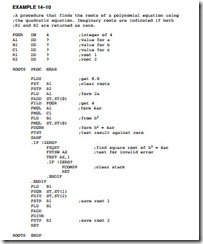
Finding the Roots Using the Quadratic Equation
This example illustrates how to find the roots of a polynomial expression (ax2 + bx + c = 0) by using the quadratic equation. The quadratic equation is:
Example 14–10 illustrates a program that finds the roots (R1 and R2) for the quadratic equation. The constants are stored in memory locations A1, B1, and C1. Note that no attempt is made to determine the roots if they are imaginary. This example tests for imaginary roots and then exits to DOS with a zero in the roots (R1 and R2), if it finds them. In practice, imaginary roots could be solved for and stored in a separate set of result memory locations.
Using a Memory Array to Store Results
The next programming example illustrates the use of a memory array and the scaled-indexed addressing mode to access the array. Example 14–11 shows a program that calculates 100 values of inductive reactance. The equation for inductive reactance is XL = 2πFL. In this example, the frequency range is from 10 Hz to 1000 Hz for F and an inductance of 4 mH. Notice how the instruction FSTP XL[ECX*4 + 4] is used to store the reactance for each frequency, beginning with the last at 1000 Hz and ending with the first at 10 Hz. Also notice how the FCOMP instruction is used to clear the stack just before the RET instruction.
Converting a Single-Precision Floating-Point Number to a String
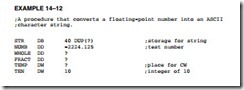
This section of the text shows how to take the floating-point contents of a 32-bit single-precision floating-point number and store it as an ASCII character string. The procedure converts the floating-point number as a mixed number with an integer part and a fractional part, separated by a decimal point. In order to simplify the procedure, a limit is placed on the size of the mixed number so the integer portion is a 32-bit binary number (±2 G) and the fraction is a 24-bit binary number (1/16M). The procedure will not function properly for larger or smaller numbers.
Example 14–12 lists a procedure that converts the contents of memory location NUMB to a string stored in the STR array. The procedure first tests the sign of the number and stores a minus sign for a negative number. After storing a minus sign, if needed, the number is made positive by the FABS instruction. Next, it is divided into an integer and fractional part and stored at WHOLE and FRACT. Notice how the FRNDINT instruction is used to round (using the chop mode) the top of the stack to form the whole number part of NUMB. The whole number part is then subtracted from the original number to generate the fractional part. This is accomplished with the FSUB instruction that subtracts the contents of ST(1) from ST.