Cache Memory
When a program executes on a computer, most of the memory references are made to a small number of locations. Typically, 90% of the execution time of a program is spent in just 10% of the code. This property is known as the locality principle. When a program references a memory location, it is likely to reference that same memory location again soon, which is known as temporal locality. Similarly, there is spatial locality, in which a memory location that is near a recently referenced location is more likely to be referenced than a memory location that is farther away. Temporal locality arises because programs spend much of their time in iteration or in recursion, and thus the same section of code is visited a disproportionately large number of times. Spatial locality arises because data tends to be stored in contiguous locations. Although 10% of the code accounts for the bulk of memory references, accesses within the 10% tend to be clustered. Thus, for a given interval of time, most of memory accesses come from an even smaller set of locations than 10% of a program’s size.
Memory access is generally slow when compared with the speed of the central processing unit (CPU), and so the memory poses a significant bottleneck in computer performance. Since most memory references come from a small set of locations, the locality principle can be exploited in order to improve performance. A small but fast cache memory, in which the contents of the most commonly accessed locations are maintained, can be placed between the main memory and the CPU. When a program executes, the cache memory is searched first, and the referenced word is accessed in the cache if the word is present. If the
referenced word is not in the cache, then a free location is created in the cache and the referenced word is brought into the cache from the main memory. The word is then accessed in the cache. Although this process takes longer than accessing main memory directly, the overall performance can be improved if a high proportion of memory accesses are satisfied by the cache.
Modern memory systems may have several levels of cache, referred to as Level 1 (L1), Level 2 (L2), and even, in some cases, Level 3 (L3). In most instances the L1 cache is implemented right on the CPU chip. Both the Intel Pentium and the IBM-Motorola PowerPC G3 processors have 32 Kbytes of L1 cache on the CPU chip.
A cache memory is faster than main memory for a number of reasons. Faster electronics can be used, which also results in a greater expense in terms of money, size, and power requirements. Since the cache is small, this increase in cost is relatively small. A cache memory has fewer locations than a main memory, and as a result it has a shallow decoding tree, which reduces the access time. The cache is placed both physically closer and logically closer to the CPU than the main memory, and this placement avoids communication delays over a shared bus.
A typical situation is shown in Figure 7-12. A simple computer without a cache
memory is shown in the left side of the figure. This cache-less computer contains a CPU that has a clock speed of 400 MHz, but communicates over a 66 MHz bus to a main memory that supports a lower clock speed of 10 MHz. A few bus cycles are normally needed to synchronize the CPU with the bus, and thus the difference in speed between main memory and the CPU can be as large as a factor of ten or more. A cache memory can be positioned closer to the CPU as shown in the right side of Figure 7-12, so that the CPU sees fast accesses over a 400 MHz direct path to the cache.
ASSOCIATIVE MAPPED CACHE
A number of hardware schemes have been developed for translating main memory addresses to cache memory addresses. The user does not need to know about the address translation, which has the advantage that cache memory enhancements can be introduced into a computer without a corresponding need for modifying application software.
The choice of cache mapping scheme affects cost and performance, and there is no single best method that is appropriate for all situations. In this section, an associative mapping scheme is studied. Figure 7-13 shows an associative map-
ping scheme for a 232 word memory space that is divided into 227 blocks of 25 = 32 words per block. The main memory is not physically partitioned in this way, but this is the view of main memory that the cache sees. Cache blocks, or cache lines, as they are also known, typically range in size from 8 to 64 bytes. Data is moved in and out of the cache a line at a time using memory interleaving (dis- cussed earlier).
The cache for this example consists of 214 slots into which main memory blocks are placed. There are more main memory blocks than there are cache slots, and any one of the 227 main memory blocks can be mapped into each cache slot (with only one block placed in a slot at a time). To keep track of which one of the 227 possible blocks is in each slot, a 27-bit tag field is added to each slot which holds an identifier in the range from 0 to 227 – 1. The tag field is the most significant 27 bits of the 32-bit memory address presented to the cache. All the tags are stored in a special tag memory where they can be searched in parallel. When- ever a new block is stored in the cache, its tag is stored in the corresponding tag memory location.
When a program is first loaded into main memory, the cache is cleared, and so while a program is executing, a valid bit is needed to indicate whether or not the slot holds a block that belongs to the program being executed. There is also a dirty bit that keeps track of whether or not a block has been modified while it is in the cache. A slot that is modified must be written back to the main memory before the slot is reused for another block.
A referenced location that is found in the cache results in a hit, otherwise, the result is a miss. When a program is initially loaded into memory, the valid bits are all set to 0. The first instruction that is executed in the program will therefore cause a miss, since none of the program is in the cache at this point. The block that causes the miss is located in the main memory and is loaded into the cache.
In an associative mapped cache, each main memory block can be mapped to any slot. The mapping from main memory blocks to cache slots is performed by partitioning an address into fields for the tag and the word (also known as the “byte” field) as shown below:
When a reference is made to a main memory address, the cache hardware inter- cepts the reference and searches the cache tag memory to see if the requested block is in the cache. For each slot, if the valid bit is 1, then the tag field of the referenced address is compared with the tag field of the slot. All of the tags are searched in parallel, using an associative memory (which is something different than an associative mapping scheme. See Section 7.8.3 for more on associative memories.) If any tag in the cache tag memory matches the tag field of the memory reference, then the word is taken from the position in the slot specified by the word field. If the referenced word is not found in the cache, then the main memory block that contains the word is brought into the cache and the referenced word is then taken from the cache. The tag, valid, and dirty fields are updated, and the program resumes execution.
Consider how an access to memory location (A035F014)16 is mapped to the cache. The leftmost 27 bits of the address form the tag field, and the remaining five bits form the word field as shown below:
If the addressed word is in the cache, it will be found in word (14)16 of a slot that has a tag of (501AF80)16, which is made up of the 27 most significant bits of the address. If the addressed word is not in the cache, then the block corresponding to the tag field (501AF80)16 will be brought into an available slot in the cache from the main memory, and the memory reference that caused the “cache miss” will then be satisfied from the cache.
Although this mapping scheme is powerful enough to satisfy a wide range of memory access situations, there are two implementation problems that limit performance. First, the process of deciding which slot should be freed when a new block is brought into the cache can be complex. This process requires a significant amount of hardware and introduces delays in memory accesses. A second problem is that when the cache is searched, the tag field of the referenced address must be compared with all 214 tag fields in the cache. (Alternative methods that limit the number of comparisons are described in Sections 7.6.2 and 7.6.3.)
Replacement Policies in Associative Mapped Caches
When a new block needs to be placed in an associative mapped cache, an avail- able slot must be identified. If there are unused slots, such as when a program begins execution, then the first slot with a valid bit of 0 can simply be used. When all of the valid bits for all cache slots are 1, however, then one of the active slots must be freed for the new block. Four replacement policies that are commonly used are: least recently used (LRU), first-in first-out (FIFO), least frequently used (LFU), and random. A fifth policy that is used for analysis purposes only, is optimal.
For the LRU policy, a time stamp is added to each slot, which is updated when any slot is accessed. When a slot must be freed for a new block, the contents of the least recently used slot, as identified by the age of the corresponding time stamp, are discarded and the new block is written to that slot. The LFU policy works similarly, except that only one slot is updated at a time by incrementing a frequency counter that is attached to each slot. When a slot is needed for a new block, the least frequently used slot is freed. The FIFO policy replaces slots in
round-robin fashion, one after the next in the order of their physical locations in the cache. The random replacement policy simply chooses a slot at random.
The optimal replacement policy is not practical, but is used for comparison purposes to determine how effective other replacement policies are to the best possible. That is, the optimal replacement policy is determined only after a program has already executed, and so it is of little help to a running program.
Studies have shown that the LFU policy is only slightly better than the random policy. The LRU policy can be implemented efficiently, and is sometimes preferred over the others for that reason. A simple implementation of the LRU pol- icy is covered in Section 7.6.7.
Advantages and Disadvantages of the Associative Mapped Cache
The associative mapped cache has the advantage that any main memory block can be placed into any cache slot. This means that regardless of how irregular the data and program references are, if a slot is available for the block, it can be stored in the cache. This results in considerable hardware overhead needed for cache bookkeeping. Each slot must have a 27-bit tag that identifies its location in main memory, and each tag must be searched in parallel. This means that in the example above the tag memory must be 27 ´ 214 bits in size, and as described above, there must be a mechanism for searching the tag memory in parallel. Memories that can be searched for their contents, in parallel, are referred to as associative, or content-addressable memories. We will discuss this kind of memory later in the chapter.
By restricting where each main memory block can be placed in the cache, we can eliminate the need for an associative memory. This kind of cache is referred to as a direct mapped cache, which is discussed in the next section.
DIRECT MAPPED CACHE
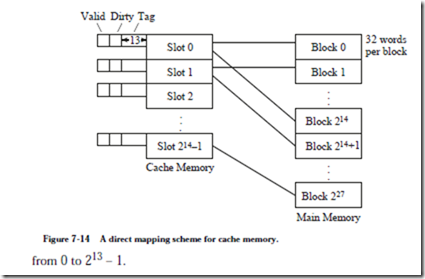
Figure 7-14 shows a direct mapping scheme for a 232 word memory. As before, the memory is divided into 227 blocks of 25 = 32 words per block, and the cache consists of 214 slots. There are more main memory blocks than there are cache slots, and a total of 227/214 = 213 main memory blocks can be mapped onto each cache slot. In order to keep track of which of the 213 possible blocks is in each slot, a 13-bit tag field is added to each slot which holds an identifier in the range
This scheme is called “direct mapping” because each cache slot corresponds to an explicit set of main memory blocks. For a direct mapped cache, each main memory block can be mapped to only one slot, but each slot can receive more than one block. The mapping from main memory blocks to cache slots is performed by partitioning an address into fields for the tag, the slot, and the word as shown below:
The 32-bit main memory address is partitioned into a 13-bit tag field, followed by a 14-bit slot field, followed by a five-bit word field. When a reference is made to a main memory address, the slot field identifies in which of the 214 slots the block will be found if it is in the cache. If the valid bit is 1, then the tag field of the referenced address is compared with the tag field of the slot. If the tag fields are the same, then the word is taken from the position in the slot specified by the word field. If the valid bit is 1 but the tag fields are not the same, then the slot is written back to main memory if the dirty bit is set, and the corresponding main memory block is then read into the slot. For a program that has just started execution, the valid bit will be 0, and so the block is simply written to the slot. The valid bit for the block is then set to 1, and the program resumes execution.
Consider how an access to memory location (A035F014)16 is mapped to the cache. The bit pattern is partitioned according to the word format shown above. The leftmost 13 bits form the tag field, the next 14 bits form the slot field, and the remaining five bits form the word field as shown below:
If the addressed word is in the cache, it will be found in word (14)16 of slot (2F80)16, which will have a tag of (1406)16.
Advantages and Disadvantages of the Direct Mapped Cache
The direct mapped cache is a relatively simple scheme to implement. The tag memory in the example above is only 13 ´ 214 bits in size, less than half of the associative mapped cache. Furthermore, there is no need for an associative search, since the slot field of the main memory address from the CPU is used to “direct” the comparison to the single slot where the block will be if it is indeed in the cache.
This simplicity comes at a cost. Consider what happens when a program references locations that are 219 words apart, which is the size of the cache. This pat- tern can arise naturally if a matrix is stored in memory by rows and is accessed by columns. Every memory reference will result in a miss, which will cause an entire block to be read into the cache even though only a single word is used. Worse still, only a small fraction of the available cache memory will actually be used.
Now it may seem that any programmer who writes a program this way deserves the resulting poor performance, but in fact, fast matrix calculations use power-of-two dimensions (which allows shift operations to replace costly multiplications and divisions for array indexing), and so the worst-case scenario of accessing memory locations that are 219 addresses apart is not all that unlikely. To avoid this situation without paying the high implementation price of a fully associative cache memory, the set associative mapping scheme can be used, which combines aspects of both direct mapping and associative mapping. Set associative mapping, which is also known as set-direct mapping, is described in the next section.