■ SUMMARY
All data in a computer is represented in terms of bits, which can be organized and interpreted as integers, fixed point numbers, floating point numbers, or characters.
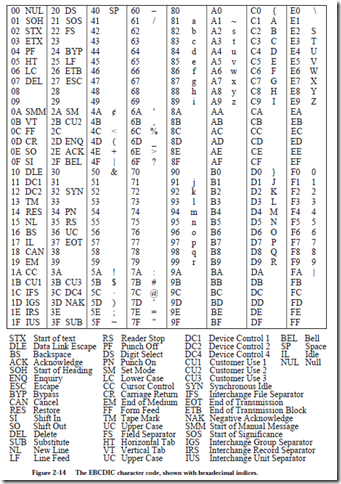
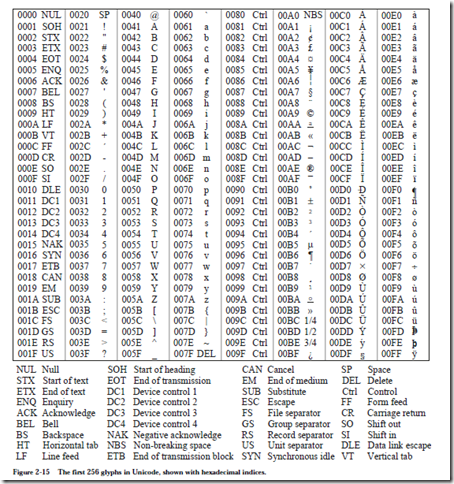
Character codes, such as ASCII, EBCDIC, and Unicode, have finite sizes and can thus be completely represented in a finite number of bits. The number of bits used for representing numbers is also finite, and as a result only a subset of the real numbers can be represented. This leads to the notions of range, precision, and error. The range for a number representation defines the largest and smallest magnitudes that can be represented, and is almost entirely determined by the base and the number of bits in the exponent for a floating point representation. The precision is determined by the number of bits used in representing the magnitude (excluding the exponent bits in a floating point representation). Error arises in floating point representations because there are real numbers that fall within the gaps between adjacent representable numbers.
■ Further Reading
(Hamacher et al., 1990) provides a good explanation of biased error in floating point representations. The IEEE 754 floating point standard is described in (IEEE, 1985). The analysis of range, error, and precision in Section 2.3 was influenced by (Forsythe, 1970). The GAO report (U.S. GAO report GAO/IMTEC-92-26) gives a very readable account of the software problem that led to the Patriot failure in Dhahran. See http://www.unicode.org for information on the Unicode standard.
■ PROBLEMS
2.1 Given a signed, fixed point representation in base 10, with three digits to the left and right of the decimal point:
a) What is the range? (Calculate the highest positive number and the lowest negative number.)
b) What is the precision? (Calculate the difference between two adjacent numbers on a number line. Remember that the error is 1/2 the precision.)
2.2 Convert the following numbers as indicated, using as few digits in the results as necessary.
a) (47)10 to unsigned binary.
b) (-27)10 to binary signed magnitude.
c) (213)16 to base 10.
d) (10110.101)2 to base 10.
e) (34.625)10 to base 4.
2.3 Convert the following numbers as indicated, using as few digits in the results as necessary.
a) (011011)2 to base 10.
b) (-27)10 to excess 32 in binary. c) (011011)2 to base 16.
d) (55.875)10 to unsigned binary. e) (132.2)4 to base 16.
2.4 Convert .2013 to decimal.
2.5 Convert (43.3)7 to base 8 using no more than one octal digit to the right of the radix point. Truncate any remainder by chopping excess digits. Use an ordinary unsigned octal representation.
2.6 Represent (17.5)10 in base 3, then convert the result back to base 10. Use two digits of precision to the right of the radix point for the intermediate base 3 form.
2.7 Find the decimal equivalent of the four-bit two’s complement number: 1000.
2.8 Find the decimal equivalent of the four-bit one’s complement number: 1111.
2.9 Show the representation for (305)10 using three BCD digits.
2.10 Show the 10’s complement representation for (-305)10 using three BCD digits.
2.11 For a given number of bits, are there more representable integers in one’s
complement, two’s complement, or are they the same?
2.12 Complete the following table for the 5-bit representations (including the sign bits) indicated below. Show your answers as signed base 10 integers.
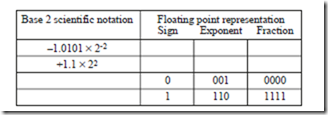
2.13 Complete the following table using base 2 scientific notation and an eight-bit floating point representation in which there is a three-bit exponent in excess 3 notation (not excess 4), and a four-bit normalized fraction with a hidden ‘1’. In this representation, the hidden 1 is to the left of the radix point. This means that the number 1.0101 is in normalized form, whereas .101 is not.
2.14 The IBM short floating point representation uses base 16, one sign bit, a seven-bit excess 64 exponent and a normalized 24-bit fraction.
a) What number is represented by the bit pattern shown below? 1 0111111 01110000 00000000 00000000 Show your answer in decimal. Note: the spaces are included in the number for readability only.
b) Represent (14.3)6 in this notation.
2.15 For a normalized floating point representation, keeping everything else the same but:
a) decreasing the base will increase / decrease / not change the number of representable numbers.
b) increasing the number of significant digits will increase / decrease / not change the smallest representable positive number.
c) increasing the number of bits in the exponent will increase / decrease / not change the range.
d) changing the representation of the exponent from excess 64 to two’s complement will increase / decrease / not change the range.
2.16 For parts (a) through (e), use a floating point representation with a sign bit in the leftmost position, followed by a two-bit two’s complement exponent, followed by a normalized three-bit fraction in base 2. Zero is represented by the bit pattern: 0 0 0 0 0 0. There is no hidden ‘1’.
a) What decimal number is represented by the bit pattern: 1 0 0 1 0 0?
b) Keeping everything else the same but changing the base to 4 will: increase / decrease / not change the smallest representable positive number.
c) What is the smallest gap between successive numbers?
d) What is the largest gap between successive numbers?
e) There are a total of six bits in this floating point representation, and there are 26 = 64 unique bit patterns. How many of these bit patterns are valid?
2.17 Represent (107.15)10 in a floating point representation with a sign bit, a seven-bit excess 64 exponent, and a normalized 24-bit fraction in base 2. There is no hidden 1. Truncate the fraction by chopping bits as necessary.
2.18 For the following single precision IEEE 754 bit patterns show the numer- ical value as a base 2 significand with an exponent (e.g. 1.11 ´ 25).
a) 0 10000011 01100000000000000000000
b) 1 10000000 00000000000000000000000
c) 1 00000000 00000000000000000000000
d) 1 11111111 00000000000000000000000
e) 0 11111111 11010000000000000000000
f ) 0 00000001 10010000000000000000000
g) 0 00000011 01101000000000000000000
2.19 Show the IEEE 754 bit patterns for the following numbers:
a) +1.1011 x 25 (single precision)
b) +0 (single precision)
c) -1.00111 x 2-1 (double precision)
d) -NaN (single precision)
2.20 Using the IEEE 754 single precision format, show the value (not the bit pattern) of:
a) The largest positive representable number (note: ¥ is not a number).
b) The smallest positive nonzero number that is normalized.
c) The smallest positive nonzero number in denormalized format.
d) The smallest normalized gap.
e) The largest normalized gap.
f) ) The number of normalized representable numbers (including 0; note that and NaN are not numbers).
2.21 Two programmers write random number generators for normalized floating point numbers using the same method. Programmer A’s generator creates random numbers on the closed interval from 0 to 1/2, and programmer B’s generator creates random numbers on the closed interval from 1/2 to 1. Programmer B’s generator works correctly, but Programmer A’s generator produces a skewed distribution of numbers. What could be the problem with Programmer A’s approach?
2.22 A hidden 1 representation will not work for base 16. Why not?
2.23 With a hidden 1 representation, can 0 be represented if all possible bit patterns in the exponent and fraction fields are used for nonzero numbers?
2.24 Given a base 10 floating point number (e.g. .583 x 103), can the number be converted into the equivalent base 2 form: .x X 2y by separately converting the fraction (.583) and the exponent (3) into base 2?