LANGUAGES AND THE MACHINE
In the last chapter we looked at the relationship between the ISA, the assembly language, and machine language. We also saw in some detail how instructions effected register transfers and the movement of data between memory and the CPU, but we touched only briefly on the actual process of assembly and program linking and loading. In this chapter we widen our view of the relationships between computer languages and the machine.
We begin by discussing compilation, the process of translating a program writ- ten in a high level language into a functionally equivalent program in assembly language. Following that, we discuss the process of assembly, the translation of an assembly language program into a functionally equivalent machine language program. We then discuss linking, the process of linking together separately assembled modules into a single program, and loading, the process of moving programs into memory and preparing them for execution. Following that, we discuss the use of assembly language macros, which can be thought of as akin to assembly-time procedures, with the exception that they are placed inline, or expanded, in the assembly language program at every location where they are invoked.
5.1 The Compilation Process
As we will see later in the chapter, the process of assembling an assembly language program into machine code is rather straightforward, because there is a one to one mapping between assembly language statements and the equivalent machine binary codes. High-level languages, on the other hand, present a much more complex problem.
5.1.1 THE STEPS OF COMPILATION
Consider a simple assignment statement
A = B + 4;
The compiler is faced with a number of fairly complex tasks in converting this statement into one or more assembly language statements:
• Reducing the program text to the basic symbols of the language, for example into identifiers such as A and B, denotations such as the constant value 4, and program delimiters such as = and +. This portion of compilation is referred to as lexical analysis.
• Parsing the symbols to recognize the underlying program structure. In the sample statement above, for example, the parser must recognize the statement as being an assignment statement of the form
Identifier “=” Expression,
where Expression is further parsed into the form
Identifier “+” Constant.
Parsing is sometimes called syntactic analysis.
• Name analysis: associating the names A and B with particular program variables, and further associating them with particular memory locations where the variables will be located at run time.
• Type analysis: determining the type of all data items. In the case above, the variables A and B, and constant 4 would be recognized as being of type int in some languages. Name and type analysis are sometimes referred to together as semantic analysis: determining the underlying meaning of pro- gram components.
• Action mapping and code generation: associating program statements with their appropriate assembly language sequence. In the statement above, the assembly language sequence might be as follows:
 • There are additional steps that the compiler must take such as allocating variables to registers, tracking register usage, and, should the programmer desire it, optimizing the program.
• There are additional steps that the compiler must take such as allocating variables to registers, tracking register usage, and, should the programmer desire it, optimizing the program.
5.1.2 THE COMPILER MAPPING SPECIFICATION
When the compiler itself is being created, information about the particular ISA must be embedded into it. (Note that the ISA on which the compiler executes does not need to be the same as the ISA code that the compiler generates, a process known as cross compilation.) This embedding is sometimes called the mapping specification for the compiler. For example, the compiler writer must decide how to map variables and constants of various types into the machine’s resources. This may be a function of both the machine and the high level language. In the C language, for example, integers (ints) can be 16, 32, or some other number of bits in size, while Java specifies that all ints be 32-bits in size. The example in the previous section, if considered for the C language, maps integers to ARC 32-bit words.
The compiler writer must also take into account the features and limitations of the machine when mapping high level language constructs to assembly language statements or statement sequences. For example, the ARC instruction set requires that all arithmetic operands must be either immediate constants or register variables. Therefore the compiler must generate code to get all variables into registers before any arithmetic instructions can be executed. This is the reason for the instruction:
In this text we concentrate on the mapping of common high level language constructs to their equivalent assembly language constructs, leaving the details of lexical and syntactic and semantic analysis to compiler texts. (Several compiler texts are described in the Further Reading section at the end of this chapter for the interested reader.)
5.1.3 HOW THE COMPILER MAPS THE THREE INSTRUCTION CLASSES INTO ASSEMBLY CODE
Let us consider in detail the mapping of the three instruction classes: data movement, arithmetic, and control flow, from high level language into assembly language. In the discussion and examples below we will use C as the example language. We choose C because of its popularity, and because its syntax and semantics, while certainly high level, are still fairly close to assembly language concepts. The reader who is unfamiliar with C should not be distracted by this choice; the syntax and semantics of C are easy to understand and carry over to other high level languages.
Variable storage in memory
In the example above, and in most of the programming examples in this text, it has been assumed that variables can be accessed directly by their name, which is mapped to a memory location that is known at the time the program is assembled, sometimes called “assembly time.” In the example above, A = B + 4, it is assumed that the variables A and B have addresses that are known when the statement is compiled. In fact, only global variables, known as static variables in C, have addresses that are known at compile time. Variables declared inside of functions or inside of blocks that are not explicitly declared as static or global only come into existence when the function or block is entered, and they disappear when the function or block is exited for the last time. These variables are called local, or in C, automatic variables. In most programs, local variables are actually much more common than global variables.
Given this ephemeral nature of local variables, a natural way of implementing them is on a last-in-first-out stack as described in Chapter 4. Variables that are stored on the stack come into existence when the stack frame is created and the function is called, and they disappear when the function is exited for the last time. While the previous chapter employed the stack pointer, %sp, to access the stack frame, it is also common to copy the contents of %sp into another register called the frame pointer %fp (also known as the base pointer) upon entry into the function, and then to use %fp to access variables on the stack frame for the duration of the function’s life. This is because temporary variables may be continually pushed and popped onto and off of the stack during the lifetime of the function, resulting in a changing offset between %sp and the items on the stack frame. Using %fp means that the compiler can define a constant offset between %fp and a value stored on the stack that will remain fixed for the life of the frame. Based addressing is used to access stack variables. For example, an ARC variable located on the stack at a location 12 bytes below %fp can loaded into register %r1 by the instruction
The use of based addressing thus allows the address arithmetic, “add the contents of %fp to -12” to be performed in a single instruction. Based addressing is so common that all popular instruction sets contain that addressing mode. Some instruction sets contain even more complicated addressing modes to assist in accessing complex data structures that are stored in the stack frame.
To emphasize the point, variables that are stored on the stack have memory addresses that are not known until run time. Their compile time addresses are known as offsets from %fp. It is only at function entry time that the actual memory address of the value is known. Thus even though stack variable addresses such as [%fp – 12] are much more common than global variable addresses such as A, we will assume global variables are used in the discussion below because of the greater ease in understanding the relationship between the high level language variable name and the address as specified in assembly language. With that provision, let us now proceed to discuss three classes of program statements: data movement, arithmetic, and control flow.
5.1.4 DATA MOVEMENT
In addition to simple scalar variables, most programming languages provide vari- ous kinds of more complex data structures, including fixed record structures such as the C struct data type, which is similar to the Pascal record, and the array data type common to most programming languages.
Structures
An example of a C struct is the representation of a point in 3-dimensional space having integer coordinates x, y, and z. In C this structure could be declared as:
An instance of this struct would be defined by the C statement
struct point pt;
Having defined point pt, the programmer can now refer to the individual components of pt by notation such as pt.x, which refers to the x component of struct pt. The compiler would lay out this structure in memory as three consecutive memory locations.
The memory address of the entire structure is taken to be the lowest, or base address of the structure, so the x component would be located at address pt, the y component at address pt + 4, and the z component at address pt + 8. Thus the y component of pt would be loaded into register %r1 by the instruction
Arrays
Most programming languages also allow the declaration of arrays of objects, that is, collections of identical components that can be referred to either individually or collectively. In C an array of ten integers can be defined with:
int A[10];
This definition would result in a collection of ten integers, indexed from 0 to 9.
The components of a struct must be explicitly named at programming time, for example, pt.z. References such as pt.i where i is a variable whose name is not determined until run time are not allowed. With arrays, on the other hand, the array index can be computed at run time. For example, the programmer may specify array element A[i], where i is a variable whose value is computed at run time and which may assume any integer value from 0 through 9. Whereas in C the index of the first element in the array always has an index of 0, other programming languages allow more flexibility. In Pascal, for example, array declarations such as:
A: array [-10..10] of integer
are permitted. This declaration would result in an array of 21 integers with indices running from -10 to +10.
Accessing array elements presents a more complicated issue because of this need to compute the index at run time, and the possibility that indices may not begin with 0. The general expression for computing the machine address of an array element at run time is given by:
where BASE is the starting address of the array, INDEX is the index of the desired element, START is the starting index of the array, and SIZE is the size of an individual element in bytes. Thus element 5 in the Pascal array declared above would have an address of A + (5 – (-10))*4 = A + 60. In ARC assembly language, assuming BASE in %r2, INDEX in %r3, START in %r4, and assuming SIZE = 4, the code to load an array value into memory would be given by
(sll is “shift left logical,” which shifts %r6 2 bits to the left is this example, bringing in two 0’s on the right.) Note that it costs three instructions to access an array element, and more if SIZE is not a power of 2. Also note that in the C programming language, which specifies that START = 0, one machine instruction is saved for each array access. This may result in a considerable savings in scientific and engineering calculations, where heavy array references are common.
5.1.5 ARITHMETIC INSTRUCTIONS
Arithmetic instructions are mapped pretty much as expected from their usage. There is a possible complication in load-store machines such as ARC and commercial RISC machines, however. Regardless of how many registers with which a machine is endowed, there is always the possibility that the compiler will encounter an arithmetic instruction that requires more registers than are avail- able. In this case the compiler must temporarily store variables on the stack, a so-called “register spill.” Compilers use sophisticated techniques to decide which registers are available, using a graph-theoretic technique known as register coloring, and to decide when the value in a register is no longer needed to store a particular value, which is known as “live-dead analysis.”
5.1.6 PROGRAM CONTROL FLOW
Most ISAs use unconditional and conditional branches, and the CPU’s arithmetic flags to implement program control flow structures. In this section we con- sider the mapping of the most common control flow statements.
The goto statement
The most trivial control flow statement is the goto statement, goto Label, which is simply implemented by the ba (branch always) unconditional branch:
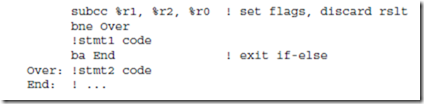
which has the meaning, “If expr yields a value of true, execute stmt1, other- wise execute stmt2.” Thus the compiler must evaluate the truth of expr, and execute one or the other of the two statements depending upon the truth or falsity of the expression. Assume for brevity in the example below that expr is (%r1 == %r2), and introducing the bne, branch if not equal instruction, then the code to implement the if-else statement is:
Note that the sign of the conditional branch, bne, branch if not equal, is the inverse of the expression, (%r1 == %r2), equals. This is because the code falls through to the stmt1 code if the condition is met, and must branch around this code if the condition is not met.
The while statement
The C while statement has the syntax:
while (expr) stmt;
The statement means, “Evaluate expr. If it is true, execute stmt, and repeat this process until expr evaluates to false.” The assembly language mapping of this statement has the interesting feature that the most efficient mapping has the expression evaluation code following the statement code. Consider the C while statement:
where again we use register variables to simplify the code. This statement is effi- ciently implemented as:
The reader can verify that placing the expression evaluation code below the statement code is more efficient than having the expression evaluation code above the statement code.
The do-while statement
C also has a do-while statement with the syntax:
do stmt while (expr);
This statement works like the while statement above except that stmt is always executed once prior to testing expr. It is implemented exactly like the while statement above except that the first ba instruction is eliminated.
The for statement
The C for statement has the syntax:
for (expr1; expr2; expr3) stmt;
The C language definition says that this statement is equivalent to:
Thus it is implemented exactly like the while statements above, with the addition of code for expr1 and expr3.