Case Study: Calculator Arithmetic Using Binary Coded Decimal
Calculator arithmetic has traditionally been done in base 10, rather than in base 2. Calculators need to be small and inexpensive, and for that reason base 10 numbers are represented in binary coded decimal (BCD – see Chapter 2) using 4 bits per BCD digit, instead of using base 2 which would require a somewhat resource-intensive base conversion. A small 4-bit ALU can then do the computations in serial fashion, BCD digit by BCD digit.
THE HP9100A CALCULATOR
The popular HP9100A calculator, which came out in the late 1960’s, performed the basic arithmetic functions: addition, subtraction, multiplication, and division, as well as square root, ex, ln x, log x, trigonometric functions, and other functions, all using base 10 arithmetic. The HP9100A is actually a desktop calculator (see Figure 3-28), but was considered small for what it accomplished with
the technology of the day. The HP9100 display shows 10 significant digits, but all calculations are performed to 12 significant digits, with the two last significant digits (which are known as guard digits) being used for truncation and round-off errors. Although the HP9100A may seem like a relic today, the arithmetic methods are still relevant.
The next two sections describe general techniques for performing fixed point and floating point BCD addition and subtraction. Other calculator operations described in the remaining sections are performed in a similar manner, making use of the addition and subtraction operations.
BINARY CODED DECIMAL ADDITION AND SUBTRACTION
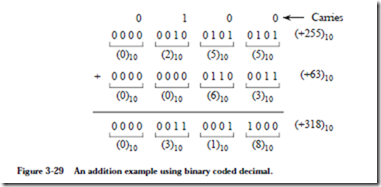
Consider adding (+255)10 and (+63)10 in BCD representation, as illustrated in Figure 3-29. Each base 10 digit occupies four bit positions, and addition is per- formed on a BCD digit by BCD digit basis (not bit by bit), from right to left, as we would normally carry it out by hand using a decimal representation. The result, (+318)10, is produced in BCD form as shown.
Subtraction in BCD is handled similar to the way subtraction is handled in two’s complement (adding the negative of the subtrahend) except that ten’s complement is used instead of two’s complement. Consider performing the subtraction operation (255 – 63 = 192)10. We can cast this into the addition problem (255 + (-63) = 192)10. We start by forming the nine’s complement of 63:
that the carry out of the highest digit position is discarded, as in two’s complement addition.
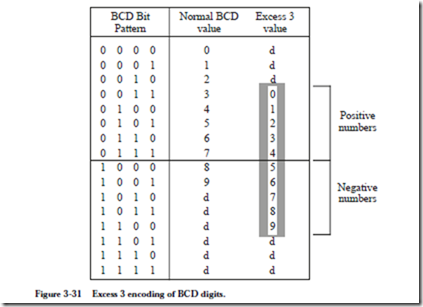
Unlike the two’s complement representation, we cannot simply look at the left- most bit to determine the sign. In ten’s complement, the number is positive if the leftmost digit is between 0 and 4, inclusive, and is negative otherwise. (The BCD bit patterns for 4 and 5 are 0100 and 0101, respectively, which both have a 0 in the leftmost bit, yet 4 indicates a positive number and 5 indicates a negative number.) If we use an excess 3 encoding for each digit, then the leftmost bit will indicate the sign. Figure 3-31 shows the encoding. Notice that six of the bit pat-
terns cannot occur, and so they are marked as don’t cares, ‘d’.
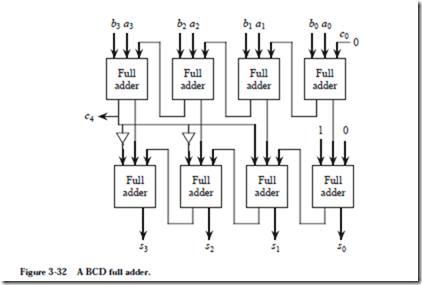
Now consider the design of a BCD full adder. The BCD full adder should sum two BCD digits and a carry-in, and should produce a sum BCD digit and a carry-out, all using excess 3. A design using two’s complement full adders is shown in Figure 3-32. The excess 3 BCD digits are added in the upper four two’s complement full adders (FAs). Since each operand is represented in excess 3, the result is in excess 6. In order to restore the result to excess 3, we need to subtract 3 from the result. As an alternative, we can add 13 to the result since 16 – 3 = 16 + 13 in a four-bit representation, discarding the carry out of the highest bit position. The latter approach is used in Figure 3-32, in which 1310 = 11012 is added to the result. Note that this only works if there is no carry. When there is a carry, then we need to also subtract 10 (or equivalently, add 6) from the result, besides subtracting 3 (or adding 13) to restore the excess 3 representation, and produce a
carry out. The approach taken here is to add 310 = 00112 for this situation, which has the same effect as adding (6 + 13) % 16 = 3, as shown in Figure 3-32.
In order to perform BCD subtraction, we can create a ten’s complement subtractor using base 10 full subtractors, as we did for the two’s complement subtractor described in Section 3.2.2. Alternatively, we can form the ten’s complement negative of the subtrahend, and then apply ordinary BCD addition. Figure 3-33
shows the computation (21 – 34 = -13)10 using the latter subtraction method for four-digit numbers. The ten’s complement negative of 34 is added to 21, which results in 9987 in ten’s complement, which is (-13)10 in signed magnitude.
BCD FLOATING POINT ADDITION AND SUBTRACTION
Consider a base 10 floating point representation with a two digit signed magnitude exponent and an eight digit signed magnitude fraction. On a calculator, a sample entry might look like:
which is in normalized form.
Now how is the number stored? A calculator user sees signed magnitude for both the exponent and the fraction, but internally, we might use a ten’s complement representation for both the exponent and the fraction. For the case above, the representation using ten’s complement would be: 88 for the exponent, and 62900000 for the fraction. Using an excess 3 representation in binary results in an exponent of 1011 1011 and a fraction of 1001 0101 1100 0011 0011 0011 0011 0011. Note that since we are using the leftmost bit for the sign, that the exponent range is [-50 to +49] and that the fraction range is [-.50000000 to +.49999999].
If we now try to represent +.9 in base 10, then we are again stuck because the leftmost bit of the fraction is used for a sign bit. That is, we cannot use 1100 in the most significant digit of the fraction, because although that is the excess 3 representation of 9, it makes the fraction appear negative. Here is a better solution: Just use ten’s complement for base 10 integer arithmetic, such as for exponents, and use signed magnitude for fractions.
Here is the summary thus far: we use a ten’s complement representation for the exponent since it is an integer, and we use a base 10 signed magnitude representation for the fraction. A separate sign bit is maintained for the fraction, so that each digit can take on any of the 10 values 0–9 (except for the first digit, which cannot be a zero) and so we can now represent +.9. We should also represent the exponent in excess 50 to make comparisons easier. The example above now looks like this internally, still in excess 3 binary form, with a two digit excess 50 exponent:
In order to add two numbers in this representation, we just go through the same steps that we did for the base 2 floating point representation described earlier. We start by adjusting the exponent and fraction of the smaller operand until the exponents of both operands are the same. If the difference in exponents is so great that the fraction of the smaller operand is shifted all the way to the right, then the smaller operand is treated as 0. After adjusting the smaller fraction, we convert either or both operands from signed magnitude to ten’s complement according to whether we are adding or subtracting, and whether the operands are positive or negative. Note that this will work now because we can treat the fractions as integers.