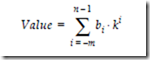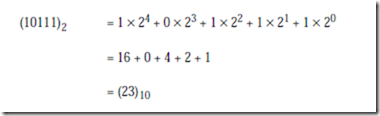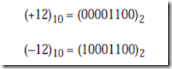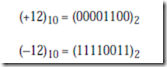DATA REPRESENTATION
2.1 Introduction
In the early days of computing, there were common misconceptions about computers. One misconception was that the computer was only a giant adding machine performing arithmetic operations. Computers could do much more than that, even in the early days. The other common misconception, in contra- diction to the first, was that the computer could do “anything.” We now know that there are indeed classes of problems that even the most powerful imaginable computer finds intractable with the von Neumann model. The correct perception, of course, is somewhere between the two.
We are familiar with computer operations that are non-arithmetic: computer graphics, digital audio, even the manipulation of the computer mouse. Regard- less of what kind of information is being manipulated by the computer, the information must be represented by patterns of 1’s and 0’s (also known as “on-off ” codes). This immediately raises the question of how that information should be described or represented in the machine—this is the data representation, or data encoding. Graphical images, digital audio, or mouse clicks must all be encoded in a systematic, agreed-upon manner.
We might think of the decimal representation of information as the most natural when we know it the best, but the use of on-off codes to represent information predated the computer by many years, in the form of Morse code.
This chapter introduces several of the simplest and most important encodings: the encoding of signed and unsigned fixed point numbers, real numbers (referred to as floating point numbers in computer jargon), and the printing characters. We shall see that in all cases there are multiple ways of encoding a given kind of data, some useful in one context, some in another. We will also take an early look at computer arithmetic for the purpose of understanding some of the encoding schemes, though we will defer details of computer arithmetic until Chapter 3.
In the process of developing a data representation for computing, a crucial issue is deciding how much storage should be devoted to each data value. For example, a computer architect may decide to treat integers as being 32 bits in size, and to implement an ALU that supports arithmetic operations on those 32-bit values that return 32 bit results. Some numbers can be too large to represent using 32 bits, however, and in other cases, the operands may fit into 32 bits, but the result of a computation will not, creating an overflow condition, which is described in Chapter 3. Thus we need to understand the limits imposed on the accuracy and range of numeric calculations by the finite nature of the data representations. We will investigate these limits in the next few sections.
2.2 Fixed Point N umbers
In a fixed point number system, each number has exactly the same number of digits, and the “point” is always in the same place. Examples from the decimal number system would be 0.23, 5.12, and 9.11. In these examples each number has 3 digits, and the decimal point is located two places from the right. Examples from the binary number system (in which each digit can take on only one of the values: 0 or 1) would be 11.10, 01.10, and 00.11, where there are 4 binary digits and the binary point is in the middle. An important difference between the way that we represent fixed point numbers on paper and the way that we represent them in the computer is that when fixed point numbers are represented in the computer the binary point is not stored anywhere, but only assumed to be in a certain position. One could say that the binary point exists only in the mind of the programmer.
We begin coverage of fixed point numbers by investigating the range and precision of fixed point numbers, using the decimal number system. We then take a look at the nature of number bases, such as decimal and binary, and how to convert between the bases. With this foundation, we then investigate several ways of representing negative fixed point numbers, and take a look at simple arithmetic operations that can be performed on them.
2.2.1 RANGE AND PRECISION IN FIXED POINT NUMBERS
A fixed point representation can be characterized by the range of expressible numbers (that is, the distance between the largest and smallest numbers) and the
precision (the distance between two adjacent numbers on a number line.) For the fixed-point decimal example above, using three digits and the decimal point placed two digits from the right, the range is from 0.00 to 9.99 inclusive of the endpoints, denoted as [0.00, 9.99], the precision is .01, and the error is 1/2 of the difference between two “adjoining” numbers, such as 5.01 and 5.02, which have a difference of .01. The error is thus .01/2 = .005. That is, we can represent any number within the range 0.00 to 9.99 to within .005 of its true or precise value.
Notice how range and precision trade off: with the decimal point on the far right, the range is [000, 999] and the precision is 1.0. With the decimal point at the far left, the range is [.000, .999] and the precision is .001.
In either case, there are only 103 different decimal “objects,” ranging from 000 to 999 or from .000 to .999, and thus it is possible to represent only 1,000 different items, regardless of how we apportion range and precision.
There is no reason why the range must begin with 0. A 2-digit decimal number can have a range of [00,99] or a range of [-50, +49], or even a range of [-99, +0]. The representation of negative numbers is covered more fully in Section 2.2.6.
Range and precision are important issues in computer architecture because both are finite in the implementation of the architecture, but are infinite in the real world, and so the user must be aware of the limitations of trying to represent external information in internal form.
2.2.2 THE ASSOCIATIVE LAW OF ALGEBRA DOES NOT ALWAYS HOLD IN COMPUTERS
In early mathematics, we learned the associative law of algebra:
a + (b + c) = (a + b) + c
As we will see, the associative law of algebra does not hold for fixed point numbers having a finite representation. Consider a 1-digit decimal fixed point representation with the decimal point on the right, and a range of [-9, 9], with a = 7, b=4, and c=–3. Now a + (b + c) = 7 + (4 + –3) = 7 + 1 =8. But (a + b) + c = (7 + 4) + –3 = 11 + –3, but 11 is outside the range of our number system! We have overflow in an intermediate calculation, but the final result is within the number system. This is every bit as bad because the final result will be wrong if an inter-mediate result is wrong.
Thus we can see by example that the associative law of algebra does not hold for finite-length fixed point numbers. This is an unavoidable consequence of this form of representation, and there is nothing practical to be done except to detect overflow wherever it occurs, and either terminate the computation immediately and notify the user of the condition, or, having detected the overflow, repeat the computation with numbers of greater range. (The latter technique is seldom used except in critical applications.)
2.2.3 RADIX NUMBER SYSTEMS
In this section, we learn how to work with numbers having arbitrary bases, although we will focus on the bases most used in digital computers, such as base 2 (binary), and its close cousins base 8 (octal), and base 16 (hexadecimal.)
The base, or radix of a number system defines the range of possible values that a digit may have. In the base 10 (decimal) number system, one of the 10 values: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 is used for each digit of a number. The most natural sys- tem for representing numbers in a computer is base 2, in which data is represented as a collection of 1’s and 0’s.
The general form for determining the decimal value of a number in a radix k fixed point number system is shown below:
The value of the digit in position i is given by bi. There are n digits to the left of the radix point and there are m digits to the right of the radix point. This form of a number, in which each position has an assigned weight, is referred to as a weighted position code. Consider evaluating (541.25)10, in which the subscript 10 represents the base. We have n = 3, m = 2, and k = 10:
Now consider the base 2 number (1010.01)2 in which n = 4, m = 2, and k = 2:
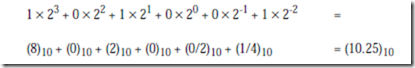This suggests how to convert a number from an arbitrary base into a base 10 number using the polynomial method. The idea is to multiply each digit by the weight assigned to its position (powers of two in this example) and then sum up the terms to obtain the converted number. Although conversions can be made among all of the bases in this way, some bases pose special problems, as we will see in the next section.
Note: in these weighted number systems we define the bit that carries the most weight as the most significant bit (MSB), and the bit that carries the least weight as the least significant bit (LSB). Conventionally the MSB is the left- most bit and the LSB the rightmost bit.
2.2.4 CONVERSIONS AMONG RADICES
In the previous section, we saw an example of how a base 2 number can be converted into a base 10 number. A conversion in the reverse direction is more involved. The easiest way to convert fixed point numbers containing both integer and fractional parts is to convert each part separately. Consider converting (23.375)10 to base 2. We begin by separating the number into its integer and fractional parts:
Converting the Integer Part of a Fixed Point Number—The Remainder Method
As suggested in the previous section, the general polynomial form for representing a binary integer is:
If we divide the integer by 2, then we will obtain:
with a remainder of b0. As a result of dividing the original integer by 2, we dis- cover the value of the first binary coefficient b0. We can repeat this process on the remaining polynomial and determine the value of b1. We can continue iterating the process on the remaining polynomial and thus obtain all of the bi. This process forms the basis of the remainder method of converting integers between bases.
We now apply the remainder method to convert (23)10 to base 2. As shown in Figure 2-1, the integer is initially divided by 2, which leaves a remainder of 0 or
1. For this case, 23/2 produces a quotient of 11 and a remainder of 1. The first remainder is the least significant binary digit (bit) of the converted number (the rightmost bit). In the next step 11 is divided by 2, which creates a quotient of 5 and a remainder of 1. Next, 5 is divided by 2, which creates a quotient of 2 and a remainder of 1. The process continues until we are left with a quotient of 0. If we continue the process after obtaining a quotient of 0, we will only obtain 0’s for the quotient and remainder, which will not change the value of the converted number. The remainders are collected into a base 2 number in the order shown in Figure 2-1 to produce the result (23)10 = (10111)2. In general, we can convert any base 10 integer to any other base by simply dividing the integer by the base to which we are converting.
We can check the result by converting it from base 2 back to base 10 using the polynomial method:
At this point, we have converted the integer portion of (23.375)10 into base 2.
Converting the Fractional Part of a Fixed Point Number—The Multiplication Method
The conversion of the fractional portion can be accomplished by successively multiplying the fraction by 2 as described below.
A binary fraction is represented in the general form:
We thus discover the coefficient b-1. If we iterate this process on the remaining fraction, then we will obtain successive bi. This process forms the basis of the multiplication method of converting fractions between bases. For the example used here (Figure 2-2), the initial fraction (.375)10 is less than 1. If we multiply it by 2, then the resulting number will be less than 2. The digit to the left of the radix point will then be 0 or 1. This is the first digit to the right of the radix point in the converted base 2 number, as shown in the figure. We repeat the process on the fractional portion until we are either left with a fraction of 0, at which point only trailing 0’s are created by additional iterations, or we have reached the limit of precision used in our representation. The digits are collected and the result is obtained: (.375)10 = (.011)2.
For this process, the multiplier is the same as the target base. The multiplier is 2 here, but if we wanted to make a conversion to another base, such as 3, then we
Non Terminating Fractions
Although this method of conversion will work among all bases, some precision can be lost in the process. For example, not all terminating base 10 fractions have a terminating base 2 form. Consider converting (.2)10 to base 2 as shown in Figure 2-3. In the last row of the conversion, the fraction .2 reappears, and the process repeats ad infinitum. As to why this can happen, consider that any non-repeating base 2 fraction can be represented as i/2k for some integers i and k. (Repeating fractions in base 2 cannot be so represented.) Algebraically,
where j is the integer i´5k. The fraction is thus non-repeating in base 10. This hinges on the fact that only non-repeating fractions in base b can be represented as i/bk for some integers i and k. The condition that must be satisfied for a non-repeating base 10 fraction to have an equivalent non-repeating base 2 fraction is:
where j = i/5k, and 5k must be a factor of i. For one digit decimal fractions, only (.0)10 and (.5)10 are non-repeating in base 2 (20% of the possible fractions); for two digit decimal fractions, only (.00)10, (.25)10, (.50)10, and (.75)10 are non-repeating (4% of the possible fractions); etc. There is a link between relatively prime numbers and repeating fractions, which is helpful in understanding why some terminating base 10 fractions do not have a terminating base 2 form. (Knuth, 1981) provides some insight in this area.
Binary versus Decimal Representations
While most computers use base 2 for internal representation and arithmetic, some calculators and business computers use an internal representation of base 10, and thus do not suffer from this representational problem. The motivation for using base 10 in business computers is not entirely to avoid the terminating fraction problem, however, but also to avoid the conversion process at the input and output units which historically have taken a significant amount of time.
Binary, Octal, and Hexadecimal Radix Representations
While binary numbers reflect the actual internal representation used in most machines, they suffer from the disadvantage that numbers represented in base 2 tend to need more digits than numbers in other bases, (why?) and it is easy to make errors when writing them because of the long strings of 1’s and 0’s. We mentioned earlier in the Chapter that base 8, octal radix, and base 16, hexadecimal radix, are related to base 2. This is due to the three radices all being divisible by 2, the smallest one. We show below that converting among the three bases 2, 8, and 16 is trivial, and there are significant practical advantages to representing numbers in these bases.
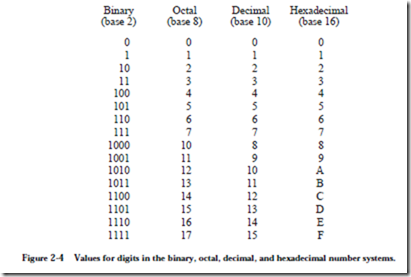
Binary numbers may be considerably wider than their base 10 equivalents. As a notational convenience, we sometimes use larger bases than 2 that are even multiples of 2. Converting among bases 2, 8, or 16 is easier than converting to and from base 10. The values used for the base 8 digits are familiar to us as base 10 digits, but for base 16 (hexadecimal) we need six more digits than are used in base 10. The letters A, B, C, D, E, F or their lower-case equivalents are commonly used to represent the corresponding values (10, 11, 12, 13, 14, 15) in hexadecimal. The digits commonly used for bases 2, 8, 10, and 16 are summarized in Figure 2-4. In comparing the base 2 column with the base 8 and base 16
columns, we need three bits to represent each base 8 digit in binary, and we need four bits to represent each base 16 digit in binary. In general, k bits are needed to represent each digit in base 2k, in which k is an integer, so base 23 = 8 uses three bits and base 24 = 16 uses four bits.
In order to convert a base 2 number into a base 8 number, we partition the base 2 number into groups of three starting from the radix point, and pad the outer- most groups with 0’s as needed to form triples. Then, we convert each triple to the octal equivalent. For conversion from base 2 to base 16, we use groups of four. Consider converting (10110)2 to base 8:
Notice that the leftmost two bits are padded with a 0 on the left in order to cre- ate a full triplet.
(Note that ‘B’ is a base 16 digit corresponding to 1110. B is not a variable.)
The conversion methods can be used to convert a number from any base to any other base, but it may not be very intuitive to convert something like (513.03)6 to base 7. As an aid in performing an unnatural conversion, we can convert to the more familiar base 10 form as an intermediate step, and then continue the conversion from base 10 to the target base. As a general rule, we use the polynomial method when converting into base 10, and we use the remainder and multi- plication methods when converting out of base 10.
2.2.5 AN EARLY LOOK AT COMPUTER ARITHMETIC
We will explore computer arithmetic in detail in Chapter 3, but for the moment, we need to learn how to perform simple binary addition because it is used in rep- resenting signed binary numbers. Binary addition is performed similar to the way we perform decimal addition by hand, as illustrated in Figure 2-5. Two binary numbers A and B are added from right to left, creating a sum and a carry in each bit position. Since the rightmost bits of A and B can each assume one of two values, four cases must be considered: 0 + 0, 0 + 1, 1 + 0, and 1 + 1, with a carry of 0, as shown in the figure. The carry into the rightmost bit position defaults to 0. For the remaining bit positions, the carry into the position can be 0
or 1, so that a total of eight input combinations must be considered as shown in the figure.
Notice that the largest number we can represent using the eight-bit format shown in Figure 2-5 is (11111111)2 = (255)10 and that the smallest number that can be represented is (00000000)2 = (0)10. The bit patterns 11111111 and 00000000 and all of the intermediate bit patterns represent numbers on the closed interval from 0 to 255, which are all positive numbers. Up to this point we have considered only unsigned numbers, but we need to represent signed numbers as well, in which (approximately) one half of the bit patterns is assigned to positive numbers and the other half is assigned to negative numbers. Four common representations for base 2 signed numbers are discussed in the next section.
2.2.6 SIGNED FIXED POINT NUMBERS
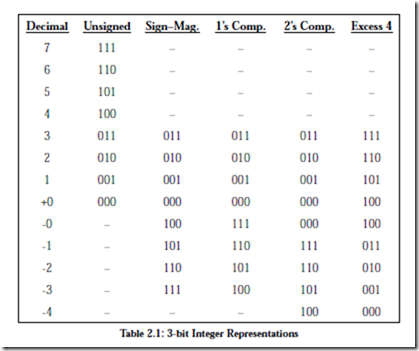
Up to this point we have considered only the representation of unsigned fixed point numbers. The situation is quite different in representing signed fixed point numbers. There are four different ways of representing signed numbers that are commonly used: sign-magnitude, one’s complement, two’s complement, and excess notation. We will cover each in turn, using integers for our examples. Throughout the discussion, the reader may wish to refer to Table 2.1 which shows for a 3-bit number how the various representations appear.
Signed Magnitude
The signed magnitude (also referred to as sign and magnitude) representation is most familiar to us as the base 10 number system. A plus or minus sign to the left of a number indicates whether the number is positive or negative as in +1210 or -1210. In the binary signed magnitude representation, the leftmost bit is used for the sign, which takes on a value of 0 or 1 for ‘+’ or ‘-’, respectively. The remaining bits contain the absolute magnitude. Consider representing (+12)10 and (-12)10 in an eight-bit format:
The negative number is formed by simply changing the sign bit in the positive number from 0 to 1. Notice that there are both positive and negative representations for zero: 00000000 and 10000000.
There are eight bits in this example format, and all bit patterns represent valid numbers, so there are 28 = 256 possible patterns. Only 28 – 1 = 255 different numbers can be represented, however, since +0 and -0 represent the same number.
We will make use of the signed magnitude representation when we look at floating point numbers in Section 2.3.
One’s Complement
The one’s complement operation is trivial to perform: convert all of the 1’s in the number to 0’s, and all of the 0’s to 1’s. See the fourth column in Table 2.1 for examples. We can observe from the table that in the one’s complement representation the leftmost bit is 0 for positive numbers and 1 for negative numbers, as it is for the signed magnitude representation. This negation, changing 1’s to 0’s and changing 0’s to 1’s, is known as complementing the bits. Consider again representing (+12)10 and (-12)10 in an eight-bit format, now using the one’s complement representation:
Note again that there are representations for both +0 and -0, which are 00000000 and 11111111, respectively. As a result, there are only 28 – 1 = 255 different numbers that can be represented even though there are 28 different bit patterns.
The one’s complement representation is not commonly used. This is at least partly due to the difficulty in making comparisons when there are two representations for 0. There is also additional complexity involved in adding numbers, which is discussed further in Chapter 3.
Two’s Complement
The two’s complement is formed in a way similar to forming the one’s complement: complement all of the bits in the number, but then add 1, and if that addition results in a carry-out from the most significant bit of the number, discard the carry-out. Examination of the fifth column of Table 2.1 shows that in the
two’s complement representation, the leftmost bit is again 0 for positive numbers and is 1 for negative numbers. However, this number format does not have the unfortunate characteristic of signed-magnitude and one’s complement representations: it has only one representation for zero. To see that this is true, con- sider forming the negative of (+0)10, which has the bit pattern:
(+0)10 = (00000000)2
Forming the one’s complement of (00000000)2 produces (11111111)2 and add- ing 1 to it yields (00000000)2, thus (-0)10 = (00000000)2. The carry out of the leftmost position is discarded in two’s complement addition (except when detecting an overflow condition). Since there is only one representation for 0, and since all bit patterns are valid, there are 28 = 256 different numbers that can be represented.
Consider again representing (+12)10 and (-12)10 in an eight-bit format, this time using the two’s complement representation. Starting with (+12)10 = (00001100)2, complement, or negate the number, producing (11110011)2. Now add 1, producing (11110100)2, and thus (-12)10 = (11110100)2:
(+12)10 = (00001100)2
(-12)10 = (11110100)2
There is an equal number of positive and negative numbers provided zero is considered to be a positive number, which is reasonable because its sign bit is 0. The positive numbers start at 0, but the negative numbers start at -1, and so the magnitude of the most negative number is one greater than the magnitude of the most positive number. The positive number with the largest magnitude is +127, and the negative number with the largest magnitude is -128. There is thus no positive number that can be represented that corresponds to the negative of -128. If we try to form the two’s complement negative of -128, then we will arrive at a negative number, as shown below:
The two’s complement representation is the representation most commonly used in conventional computers, and we will use it throughout the book.
Excess Representation
In the excess or biased representation, the number is treated as unsigned, but is “shifted” in value by subtracting the bias from it. The concept is to assign the smallest numerical bit pattern, all zeros, to the negative of the bias, and assign the remaining numbers in sequence as the bit patterns increase in magnitude. A convenient way to think of an excess representation is that a number is represented as the sum of its two’s complement form and another number, which is known as the “excess,” or “bias.” Once again, refer to Table 2.1, the rightmost column, for examples.
Consider again representing (+12)10 and (-12)10 in an eight-bit format but now using an excess 128 representation. An excess 128 number is formed by adding 128 to the original number, and then creating the unsigned binary version. For (+12)10, we compute (128 + 12 = 140)10 and produce the bit pattern (10001100)2. For (-12)10, we compute (128 + -12 = 116)10 and produce the bit pattern (01110100)2:
(+12)10 = (10001100)2
(-12)10 = (01110100)2
Note that there is no numerical significance to the excess value: it simply has the effect of shifting the representation of the two’s complement numbers.
There is only one excess representation for 0, since the excess representation is simply a shifted version of the two’s complement representation. For the previous case, the excess value is chosen to have the same bit pattern as the largest negative number, which has the effect of making the numbers appear in numerically sorted order if the numbers are viewed in an unsigned binary representation. Thus, the most negative number is (-128)10 = (00000000)2 and the most posi- tive number is (+127)10 = (11111111)2. This representation simplifies making comparisons between numbers, since the bit patterns for negative numbers have numerically smaller values than the bit patterns for positive numbers. This is important for representing the exponents of floating point numbers, in which exponents of two numbers are compared in order to make them equal for addition and subtraction. We will explore floating point representations in Section 2.3.
2.2.7 BINARY CODED DECIMAL
Numbers can be represented in the base 10 number system while still using a binary encoding. Each base 10 digit occupies four bit positions, which is known as binary coded decimal (BCD). Each BCD digit can take on any of 10 values. There are 24 = 16 possible bit patterns for each base 10 digit, and as a result, six bit patterns are unused for each digit. In Figure 2-6, there are four decimal significant digits, so 104 = 10,000 bit patterns are valid, even though 216 = 65,536 bit patterns are possible with 16 bits.
Although some bit patterns are unused, the BCD format is commonly used in calculators and in business applications. There are fewer problems in representing terminating base 10 fractions in this format, unlike the base 2 representation. There is no need to convert data that is given at the input in base 10 form (as in a calculator) into an internal base 2 representation, or to convert from an internal representation of base 2 to an output form of base 10.
Performing arithmetic on signed BCD numbers may not be obvious. Although we are accustomed to using a signed magnitude representation in base 10, a different method of representing signed base 10 numbers is used in a computer. In the nine’s complement number system, positive numbers are represented as in ordinary BCD, but the leftmost digit is less than 5 for positive numbers and is 5 or greater for negative numbers. The nine’s complement negative is formed by subtracting each digit from 9. For example, the base 10 number +301 is represented as 0301 (or simply 301) in both nine’s and ten’s complement as shown in Figure 2-6a. The nine’s complement negative is 9698 (Figure 2-6b), which is obtained by subtracting each digit in 0301 from 9.
The ten’s complement negative is formed by adding 1 to the nine’s complement negative, so the ten’s complement representation of -301 is then 9698 + 1 = 9699 as shown in Figure 2-6c. For this example, the positive numbers range from 0 – 4999 and the negative numbers range from 5000 to 9999.