2.3 Floating Point N umbers
The fixed point number representation, which we explored in Section 2.2, has a fixed position for the radix point, and a fixed number of digits to the left and right of the radix point. A fixed point representation may need a great many dig- its in order to represent a practical range of numbers. For example, a computer that can represent a number as large as a trillion1 maintains at least 40 bits to the left of the radix point since 240 » 1012. If the same computer needs to represent one trillionth, then 40 bits must also be maintained to the right of the radix point, which results in a total of 80 bits per number.
In practice, much larger numbers and much smaller numbers appear during the course of computation, which places even greater demands on a computer. A great deal of hardware is required in order to store and manipulate numbers with 80 or more bits of precision, and computation proceeds more slowly for a large number of digits than for a small number of digits. Fine precision, however, is generally not needed when large numbers are used, and conversely, large numbers do not generally need to be represented when calculations are made with small numbers. A more efficient computer can be realized when only as much precision is retained as is needed.
2.3.1 RANGE AND PRECISION IN FLOATING POINT NUMBERS
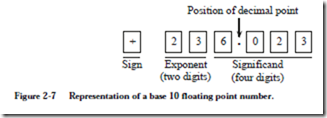
A floating point representation allows a large range of expressible numbers to be represented in a small number of digits by separating the digits used for precision from the digits used for range. The base 10 floating point number representing Avogadro’s number is shown below:
1. In the American number system, which is used here, a trillion = 1012. In the British number system, this is a “million million,” or simply a “billion.” The British “milliard,” or a “thou- sand million” is what Americans call a “billion.”
Here, the range is represented by a power of 10, 1023 in this case, and the precision is represented by the digits in the fixed point number, 6.023 in this case. In discussing floating point numbers, the fixed point part is often referred to as the mantissa, or significand of the number. Thus a floating point number can be characterized by a triple of numbers: sign, exponent, and significand.
The range is determined primarily by the number of digits in the exponent (two digits are used here) and the base to which it is raised (base 10 is used here) and the precision is determined primarily by the number of digits in the significand (four digits are used here). Thus the entire number can be represented by a sign and 6 digits, two for the exponent and four for the significand. Figure 2-7 shows how the triple of sign, exponent, significand, might be formatted in a computer.
Notice how the digits are packed together with the sign first, followed by the exponent, followed by the significand. This ordering will turn out to be helpful in comparing two floating point numbers. The reader should be aware that the decimal point does not need to be stored with the number as long as the decimal point is always in the same position in the significand. (This will be discussed in Section 2.3.2.)
If we need a greater range, and if we are willing to sacrifice precision, then we can use just three digits in the fraction and have three digits left for the exponent without increasing the number of digits used in the representation. An alternative method of increasing the range is to increase the base, which has the effect of increasing the precision of the smallest numbers but decreasing the precision of the largest numbers. The range/precision trade-off is a major advantage of using a floating point representation, but the reduced precision can cause problems, sometimes leading to disaster, an example of which is described in Section 2.4.
2.3.2 NORMALIZATION, AND THE HIDDEN BIT
A potential problem with representing floating point numbers is that the same number can be represented in different ways, which makes comparisons and arithmetic operations difficult. For example, consider the numerically equivalent forms shown below:
In order to avoid multiple representations for the same number, floating point numbers are maintained in normalized form. That is, the radix point is shifted to the left or to the right and the exponent is adjusted accordingly until the radix point is to the left of the leftmost nonzero digit. So the rightmost number above is the normalized one. Unfortunately, the number zero cannot be represented in this scheme, so to represent zero an exception is made. The exception to this rule is that zero is represented as all 0’s in the mantissa.
If the mantissa is represented as a binary, that is, base 2, number, and if the normalization condition is that there is a leading “1” in the normalized mantissa, then there is no need to store that “1” and in fact, most floating point formats do not store it. Rather, it is “chopped off ” before packing up the number for storage, and it is restored when unpacking the number into exponent and mantissa. This results in having an additional bit of precision on the right of the number, due to removing the bit on the left. This missing bit is referred to as the hidden bit, also known as a hidden 1. For example, if the mantissa in a given format is .11010 after normalization, then the bit pattern that is stored is 1010—the left-most bit is truncated, or hidden. We will see that the IEEE 754 floating point format uses a hidden bit.
2.3.3 REPRESENTING FLOATING POINT NUMBERS IN THE COM- PUTER—PRELIMINARIES
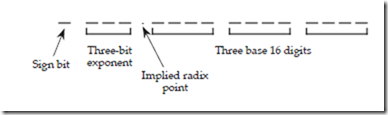
Let us design a simple floating point format to illustrate the important factors in representing floating point numbers on the computer. Our format may at first seem to be unnecessarily complex. We will represent the significand in signed magnitude format, with a single bit for the sign bit, and three hexadecimal digits for the magnitude. The exponent will be a 3-bit excess-4 number, with a radix of 16. The normalized form of the number has the hexadecimal point to the left of the three hexadecimal digits.
The bits will be packed together as follows: The sign bit is on the left, followed by the 3-bit exponent, followed by the three hexadecimal digits of the significand. Neither the radix nor the hexadecimal point will be stored in the packed form.
The reason for these rather odd-seeming choices is that numbers in this format can be compared for ![]() in their “packed” format, which is shown in the illustration below:
in their “packed” format, which is shown in the illustration below:
 Consider representing (358)10 in this format.
Consider representing (358)10 in this format.
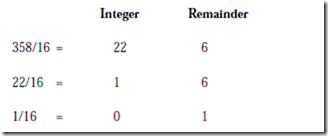
The first step is to convert the fixed point number from its original base into a fixed point number in the target base. Using the method described in Section 2.1.3, we convert the base 10 number into a base 16 number as shown below:
Thus (358)10 = (166)16. The next step is to convert the fixed point number into a floating point number:
Note that the form 160 reflects a base of 16 with an exponent of 0, and that the number 16 as it appears on the page uses a base 10 form. That is, (160)10 = (100)16. This is simply a notational convenience used in describing a floating point number.
The next step is to normalize the number:
Finally, we fill in the bit fields of the number. The number is positive, and so we place a 0 in the sign bit position. The exponent is 3, but we represent it in excess 4, so the bit pattern for the exponent is computed as shown below:
Alternatively, we could have simply computed 3 + 4 = 7 in base 10, and then made the equivalent conversion (7)10 = (111)2.
Finally, each of the base 16 digits is represented in binary as 1 = 0001, 6 = 0110, and 6 = 0110. The final bit pattern is shown below:
Notice again that the radix point is not explicitly represented in the bit pattern, but its presence is implied. The spaces between digits are for clarity only, and do not suggest that the bits are stored with spaces between them. The bit pattern as stored in a computer’s memory would look like this:
0111000101100110
The use of an excess 4 exponent instead of a two’s complement or a signed magnitude exponent simplifies addition and subtraction of floating point numbers (which we will cover in detail in Chapter 3). In order to add or subtract two normalized floating point numbers, the smaller exponent (smaller in degree, not magnitude) must first be increased to the larger exponent (this retains the range), which also has the effect of unnormalizing the smaller number. In order to deter- mine which exponent is larger, we only need to treat the bit patterns as unsigned numbers and then make our comparison. That is, using an excess 4 representation, the smallest exponent is -4, which is represented as 000. The largest exponent is +3, which is represented as 111. The remaining bit patterns for -3, -2, -1, 0, +1, and +2 fall in their respective order as 001, 010, 011, 100, 101, and 110.
Now if we are given the bit pattern shown above for (358)10 along with a description of the floating point representation, then we can easily determine the number. The sign bit is a 0, which means that the number is positive. The exponent in unsigned form is the number (+7)10, but since we are using excess 4, we
must subtract 4 from it, which results in an actual exponent of (+7 – 4 = +3)10. The fraction is grouped in four-bit hexadecimal digits, which gives a fraction of (.166)16. Putting it all together results in (+.166 ´ 163)16 = (358)10.
Now suppose that only 10 bits are allowed for the fraction in the above example, instead of the 12 bits that group evenly into fours for hexadecimal digits. How does the representation change? One approach might be to round the fraction and adjust the exponent as necessary. Another approach, which we use here, is to simply truncate the least significant bits by chopping and avoid making adjustments to the exponent, so that the number we actually represent is:
If we treat the missing bits as 0’s, then this bit pattern represents (.164 ´ 163)16. This method of truncation produces a biased error, since values of 00, 01, 10, and 11 in the missing bits are all treated as 0, and so the error is in the range from 0 to (.003)16. The bias comes about because the error is not symmetric about 0. We will not explore the bias problem further here, but a more thorough discussion can be found in (Hamacher et al., 1990).
We again stress that whatever the floating point format is, that it be known to all parties that intend to store or retrieve numbers in that format. The Institute of Electrical and Electronics Engineers (IEEE), has taken the lead in standardizing floating point formats. The IEEE 754 floating point format, which is in nearly universal usage, is discussed in Section 2.3.5.
2.3.4 ERROR IN FLOATING POINT REPRESENTATIONS
The fact that finite precision introduces error means that we should consider how great the error is (by “error”, we mean the distance between two adjacent representable numbers), and whether it is acceptable for our application. As an example of a potential pitfall, consider representing one million in floating point, and then subtracting one million 1’s from it. We may still be left with a million if the error is greater than 1.1
In order to characterize error, range, and precision, we use the following notation:
The number of significant digits in the fraction is represented by s, which is different than the number of bits in the fraction if the base is anything other than 2 (for example, base 16 uses four bits for each digit). In general, if the base is 2k where k is an integer, then k bits are needed to represent each digit. The use of a hidden 1 increases s by one bit even though it does not increase the number of representable numbers. In the previous example, there are three significant digits in the base 16 fraction and there are 12 bits that make up the three digits. There are three bits in the excess 4 exponent, which gives an exponent range of [-22 to 22 – 1]. For this case, b = 16, s = 3, M = 3, and m = -4.
In the analysis of a floating point representation, there are five characteristics that we consider: the number of representable numbers, the numbers that have the largest and smallest magnitudes (other than zero), and the sizes of the largest and smallest gaps between successive numbers.
The number of representable numbers can be determined as shown in Figure
2-8. The sign bit can take on two values, as indicated by the position marked
with an encircled “A.” The total number of exponents is indicated in position B. Note that not all exponent bit patterns are valid in all representations. The IEEE 754 floating point standard, which we will study shortly, has a smallest exponent of -126 even though the eight-bit exponent can support a number as small as -128. The forbidden exponents are reserved for special numbers, such as zero and infinity.
The first digit of the fraction is considered next, which can take on any value except 0 in a normalized representation (except when a hidden 1 is used) as indicated by (b – 1) at position C. The remaining digits of the fraction can take on any of the b values for the base, as indicated by bs-1 at position D. If a hidden 1 is used, then position C is removed and position 4 is replaced with bs. Finally, there must be a representation for 0, which is accounted for in position E.
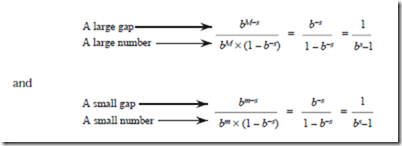
Consider now the numbers with the smallest and largest magnitudes. The number with the smallest magnitude has the smallest exponent and the smallest non- zero normalized fraction. There must be a nonzero value in the first digit, and
since a 1 is the smallest value we can place there, the smallest fraction is b-1. The number with the smallest magnitude is then bm·b-1 = bm-1. Similarly, the number with the largest magnitude has the largest exponent and the largest fraction (when the fraction is all 1’s), which is equal to bM ·(1 – b–s).
The smallest and largest gaps are computed in a similar manner. The smallest gap occurs when the exponent is at its smallest value and the least significant bit of the fraction changes. This gap is bm·b–s = bm–s. The largest gap occurs when the exponent is at its largest value and the least significant bit of the fraction changes. This gap is bM·b–s = bM–s.
As an example, consider a floating point representation in which there is a sign bit, a two-bit excess 2 exponent, and a three-bit normalized base 2 fraction in which the leading 1 is visible; that is, the leading 1 is not hidden. The representation of 0 is the bit pattern 000000. A number line showing all possible numbers that can be represented in this format is shown in Figure 2-9. Notice that there is
a relatively large gap between 0 and the first representable number, because the normalized representation does not support bit patterns that correspond to num- bers between 0 and the first representable number.
The smallest representable number occurs when the exponent and the fraction are at their smallest values. The smallest exponent is -2, and the smallest normal- ized fraction is (.100)2. The smallest representable number is then bm´b-1 = bm-1 = 2-2-1 = 1/8.
Similarly, the largest representable number occurs when the exponent and the fraction are both at their largest values. The largest fraction occurs when the fraction is all 1’s, which is a number that is 2-3 less than 1 since there are three digits in the fraction. The largest representable number is then bM ´(1 – b–s) = 21 ´ (1 – 2-3) = 7/4.
The smallest gap occurs when the exponent is at its smallest value and the least significant bit of the fraction changes, which is bm´b–s = bm–s = 2-2-3 = 1/32.
Similarly, the largest gap occurs when the exponent is at its largest value and the least significant bit of the fraction changes, which is bM´b–s = bM–s = 21-3 = 1/4.
The number of bit patterns that represent valid numbers is less than the number of possible bit patterns, due to normalization. As discussed earlier, the number of representable numbers consists of five parts, which take into account the sign bit, the exponents, the first significant digit, the remaining digits, and the bit pattern for 0. This is computed as shown below:
Notice that the gaps are small for small numbers and that the gaps are large for large numbers. In fact, the relative error is approximately the same for all numbers. If we take the ratio of a large gap to a large number, and compare that to the ratio of a small gap to a small number, then the ratios are the same:
The representation for a “small number” is used here, rather than the smallest number, because the large gap between zero and the first representable number is a special case.
EXAMPLE
Consider the problem of converting (9.375 ´ 10-2)10 to base 2 scientific notation. That is, the result should have the form x.yy ´ 2z. We start by converting from
base 10 floating point to base 10 fixed point by moving the decimal point two positions to the left, which corresponds to the -2 exponent: .09375. We then convert from base 10 fixed point to base 2 fixed point by using the multiplication method:
2.3.5 THE IEEE 754 FLOATING POINT STANDARD
There are many ways to represent floating point numbers, a few of which we have already explored. Each representation has its own characteristics in terms of range, precision, and the number of representable numbers. In an effort to improve software portability and ensure uniform accuracy of floating point calculations, the IEEE 754 floating point standard for binary numbers was developed (IEEE, 1985). There are a few entrenched product lines that predate the standard that do not use it, such as the IBM/370, the DEC VAX, and the Cray line, but virtually all new architectures generally provide some level of IEEE 754 support.
The IEEE 754 standard as described below must be supported by a computer sys- tem, and not necessarily by the hardware entirely. That is, a mixture of hardware and software can be used while still conforming to the standard.
2.3.5.1Formats
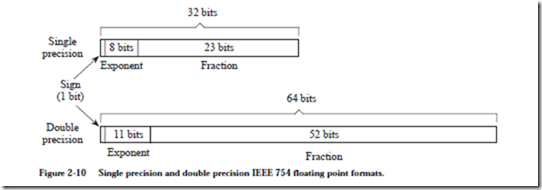
There are two primary formats in the IEEE 754 standard: single precision and double precision. Figure 2-10 summarizes the layouts of the two formats. The
single precision format occupies 32 bits, whereas the double precision format occupies 64 bits. The double precision format is simply a wider version of the
single precision format.
The sign bit is in the leftmost position and indicates a positive or negative number for a 0 or a 1, respectively. The 8-bit excess 127 (not 128) exponent follows, in which the bit patterns 00000000 and 11111111 are reserved for special cases, as described below. For double precision, the 11-bit exponent is represented in excess 1023, with 00000000000 and 11111111111 reserved. The 23-bit base 2 fraction follows. There is a hidden bit to the left of the binary point, which when taken together with the single-precision fraction form a 23 + 1 = 24-bit significand of the form 1.fff…f where the fff…f pattern represents the 23-bit fractional part that is stored. The double-precision format also uses a hidden bit to the left of the binary point, which supports a 52 + 1 = 53 bit significand. For both for- mats, the number is normalized unless denormalized numbers are supported, as described later.
There are five basic types of numbers that can be represented. Nonzero normalized numbers take the form described above. A so-called “clean zero” is represented by the reserved bit pattern 00000000 in the exponent and all 0’s in the fraction. The sign bit can be 0 or 1, and so there are two representations for zero:
+0 and -0.
Infinity has a representation in which the exponent contains the reserved bit pat- tern 11111111, the fraction contains all 0’s, and the sign bit is 0 or 1. Infinity is useful in handling overflow situations or in giving a valid representation to a number (other than zero) divided by zero. If zero is divided by zero or infinity is divided by infinity, then the result is undefined. This is represented by the NaN (not a number) format in which the exponent contains the reserved bit pattern 11111111, the fraction is nonzero and the sign bit is 0 or 1. A NaN can also be produced by attempting to take the square root of -1.
As with all normalized representations, there is a large gap between zero and the first representable number. The denormalized, “dirty zero” representation allows numbers in this gap to be represented. The sign bit can be 0 or 1, the exponent contains the reserved bit pattern 00000000 which represents -126 for single pre- cision (-1022 for double precision), and the fraction contains the actual bit pat- tern for the magnitude of the number. Thus, there is no hidden 1 for this format. Note that the denormalized representation is not an unnormalized representation. The key difference is that there is only one representation for each denormalized number, whereas there are infinitely many unnormalized representations.
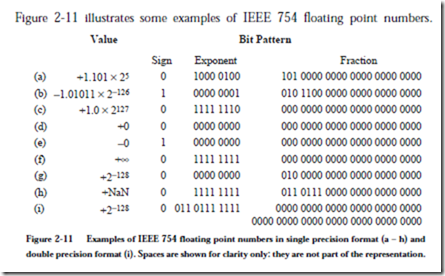
Figure 2-11 illustrates some examples of IEEE 754 floating point numbers.
Examples (a) through (h) are in single precision format and example (i) is in double precision format. Example (a) shows an ordinary single precision number. Notice that the significand is 1.101, but that only the fraction (101) is explicitly represented. Example (b) uses the smallest single precision exponent (–126) and example (c) uses the largest single precision exponent (127).
Examples (d) and (e) illustrate the two representations for zero. Example (f ) illustrates the bit pattern for +¥. There is also a corresponding bit pattern for –¥. Example (g) shows a denormalized number. Notice that although the number itself is 2-128, the smallest representable exponent is still -126. The exponent for single precision denormalized numbers is always -126, which is represented by the bit pattern 00000000 and a nonzero fraction. The fraction represents the magnitude of the number, rather than a significand. Thus we have +2-128 = +.01 ´ 2–126, which is represented by the bit pattern shown in Figure 2-11g.
Example (h) shows a single precision NaN. A NaN can be positive or negative. Finally, example (i) revisits the representation of 2–128 but now using double precision. The representation is for an ordinary double precision number and so there are no special considerations here. Notice that 2–128 has a significand of 1.0, which is why the fraction field is all 0’s.
In addition to the single precision and double precision formats, there are also single extended and double extended formats. The extended formats are not visible to the user, but they are used to retain a greater amount of internal precision during calculations to reduce the effects of roundoff errors. The extended formats increase the widths of the exponents and fractions by a number of bits that can vary depending on the implementation. For instance, the single extended format adds at least three bits to the exponent and eight bits to the fraction. The double extended format is typically 80 bits wide, with a 15-bit exponent and a 64-bit fraction.
2.3.5.2Rounding
An implementation of IEEE 754 must provide at least single precision, whereas the remaining formats are optional. Further, the result of any single operation on floating point numbers must be accurate to within half a bit in the least significant bit of the fraction. This means that some additional bits of precision may need to be retained during computation (referred to as guard bits), and there must be an appropriate method of rounding the intermediate result to the number of bits in the fraction.
There are four rounding modes in the IEEE 754 standard. One mode rounds to 0, another rounds toward +¥, and another rounds toward -¥. The default mode rounds to the nearest representable number. Halfway cases round to the number whose low order digit is even. For example, 1.01101 rounds to 1.0110 whereas 1.01111 rounds to 1.1000.