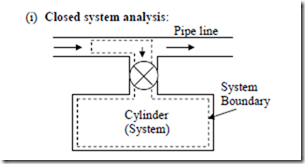
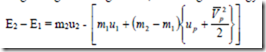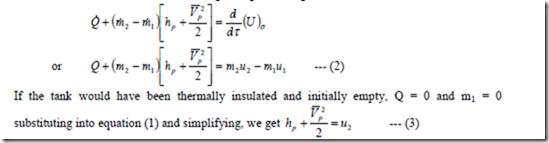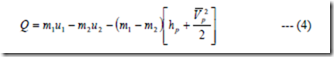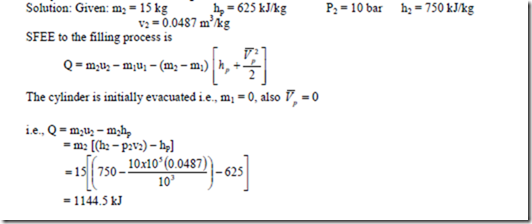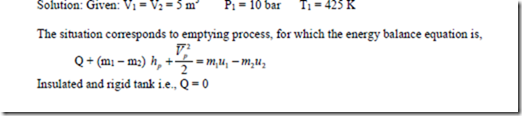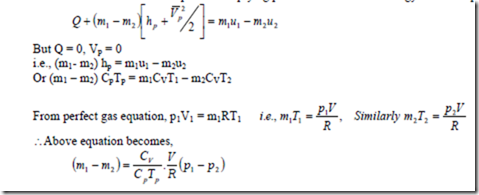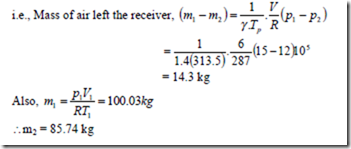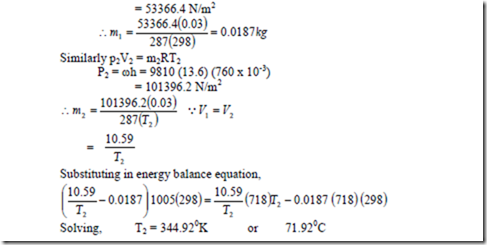Unsteady flow process

Unsteady flow process: In a steady flow process we have assumed that the mass and energy within the system remain constant and do not vary with time. In an unsteady flow process, mass and energy within the control volume vary continuously. The fluid flow into and out of the system.

Example: Filling or evacuation of a tank, (internal energy as well as mass of the tank changes with time), the condition of water in the cylinder jacket of an I.C. engine (is time dependant)

Analysis: Consider the flow of a fluid through a pipe line into the cylinder. Let m1 be the mass of the fluid initially in the cylinder at pressure p1, temperature t1 and m2 the final mass in the cylinder at pressure p2, temperature t2. The mass that flows into the cylinder is thus (m2 – m1).

There are two ways for solving problems involving unsteady flow (i) Closed system analysis (ii) Control volume analysis

Since no mass crosses the boundary of the system, the boundary of the system is selected in such a way that it includes not only the cylinder but also that portion of the fluid in the pipe line which will be introduced eventually into the cylinder as shown in figure. That means the system has variable boundaries which at the final state will be the same as that of the cylinder. Initially energy of the system E1 is composed of the internal energy of the mass initially in the cylinder, m1u1 plus the energy of the fluid which will eventually flow

the pipe line into the cylinder, (m2 – m1) where the subscript ‘p’ refers to the condition of the fluid in the pipe line. At the final state, energy E2 of the fluid in the system will be equal to m2u2.

Neglecting the change in PE, the change in energy is,

To find out work done on the system, consider a mass in the pipe line (m2 – m1) which is subjected to a controlled pressure Pp. The flow work due to the flow of mass (m2 – m1) into the cylinder from the (m2 – m1) vp in the pipe line to a zero volume is

W = Pp [0 – (m2 – m1) vp] = – (m2 – m1) Pp vp

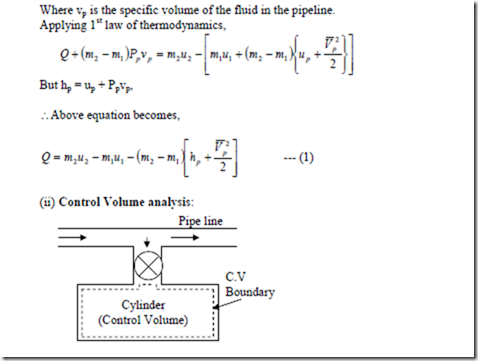
Where vp is the specific volume of the fluid in the pipeline. Applying 1st law of thermodynamics,

The cylinder itself is taken as the control volume as shown in figure. In this case, there is no work interaction. Using the general equation 1st law and considering no mass flows out of the control volume and neglecting the change in PE, as in the earlier case we have

Also if KE in the pipe line is not appreciable, hp = u2 i.e., the specific enthalpy of the fluid in the pipe line is equal to the specific internal energy of the fluid in the cylinder at the final state.

Note: The tank emptying process is the reverse of filling process i.e., there is flow of fluid from the tank (cylinder) to the surroundings.

Analogous to filling process, applying 1st law, of thermodynamics, we have

Where hp and Vp are the specific enthalpy and velocity of leaving fluid.

For no heat transfer and negligible exit velocity,
(m1 – m2) hp = m1u1 – m2u2
Further if the tank is to be fully emptied (m2 = 0)
i.e., m1hp = m1u1
or hp = u1

i.e., the specific enthalpy of the fluid in the cylinder is equal to the specific internal energy of the fluid in the pipe line at the final state.

Problems:

1. A household gas cylinder initially evacuated is filled by 15 kg gas supply of enthalpy 625 kJ/kg. After filling, the gas in the cylinder has the following parameters: pressure 10 bar, enthalpy 750 kJ/kg and specific volume 0.0487 m3/kg. Evaluate the heat received by the cylinder from the surroundings.

2. An insulated and rigid tank contains 5 m3 of air at 10 bar and 425 K. The air is then let off to atmosphere through a valve. Determine the work obtainable by utilizing the KE of the discharge air. Take Cp = 1 kJ/kg K, CV = 0.714 kJ/kg0-K atmosphere pressure = 1 bar.

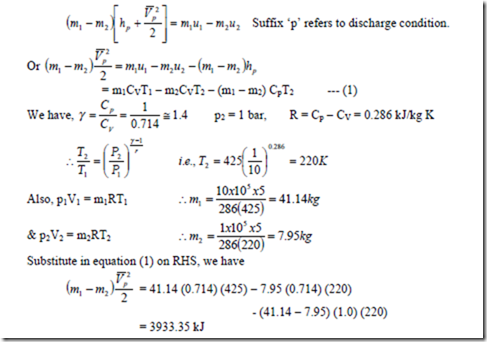3. A vessel of constant volume 0.3 m3 contains air at 1.5 bar and is connected via a valve, to a large main carrying air at a temperature of 380C and high pressure. The valve is opened allowing air to enter the vessel and raising the pressure there in to 7.5 bar. Assuming the vessel and valve to be thermally insulated, find the mass of air entering the vessel.

Solution: The situation corresponds to filling process, for which the energy balance equation is,

= 1.44 kg

= Mass of the air entering

4. After the completion of exhaust stroke of an I.C. engine the piston cylinder assembly remains filled up with 1 x 10-4kg of combustible products at 800 K. During the subsequent suction stroke, the piston moves outward and 16 x 10-4 kg of air at 290 K is sucked inside the cylinder. The suction process occurs at constant pressure and heat interaction is negligible. Evaluate the temperature of gases at the end of suction stroke. For air and gases, take Cp = 1kJ/kg

5. An air receiver of volume 6 m3 contains air at 15 bar and 40.50C. A valve is opened and some air is allowed to blow out to atmosphere. The pressure of the air in the receiver drops rapidly to 12 bar when the valve is then closed. Calculate the mass of air which has left the receiver.

Solution: The situation correspond to emptying process for which the energy balance equation is,

6. The internal energy of air is given, at ordinary temperature by, u = u0 + 0.718t. Where u is in kJ/kg, u0 is any arbitrary value of u at 00C, kJ/kg and t is temperature in 0C. Also for air, pv = 0.287 (t + 273) where p is in KPa and v is in m3/kg.

i) An evacuated bottle is fitted with a valve through which air from the atmosphere, at 760 mm oxygen and 250C, is allowed to flow slowly to fill the bottle. If no heat transfer to or from the air in the bottle, what will its temperature be when the pressure in the bottle reaches 760 mm Hg?

ii) If the bottle initially contains 0.03 m3 of air at 400 mm Hg and 250C, what will the temperature be when the pressure in the bottle reaches 760 mm of Hg?

7. The internal energy of air is given by u = u0 + 0.718 t also for air, pv = 0.287 (t + 273). A mass of air is stirred by a paddle wheel in an insulated constant volume tank. The velocities due to stirring make a negligible contribution to the internal energy of the air. Air flows out through a small valve in the tank at a rate controlled to keep the temperature in the tank constant. At a certain instant the conditions are as follows: tank volume 0.12m3, pressure 1 MPa, temperature 1500C and power to paddle wheel 0.1 kW. Find the rate of flow of air out of the tank at this instant.

8. A certain water heater operates under steady flow conditions receiving 4.2 kg/s of water at 750C temperature, enthalpy 314 kJ/kg. The water is heated by mixing with steam which is supplied to the heater at temperature 1000C and enthalpy 2676 kJ/kg. The mixture leaves the heater as liquid water at temperature 1000C and enthalpy 419 kJ/kg. How much steam must be supplied to the heater per hour.

9. In a water cooling tower air enters at a height of 1 m above the ground level with velocity of 20 m/s and leaves the tower at a height of 7 m above the ground level with a velocity of 30 m/s. Water enters the tower at a height of 8 m above the ground level with a velocity of 3 m/s and leaves the tower at a height of 0.8 m with a velocity of 1 m/s. Water temperatures at inlet and exit are 800C and 500C respectively, while the inlet and exit temperatures of air are 300C and 700C respectively. The cooling tower is well insulated and a of 2.25 kW drives the air through the cooling tower. Determine the mass flow rate of air required if the mass flow rate of water is 1.5 kg/s.

Assume that for air Cp = 1.005 kJ/kg-0K and for water C = 4.187 kJ/kg-0K.

Steam and Hydronic Line Controls:Thermodynamic Steam Traps

Hydronic Systems

Pipework and oil traps:Discharge line mufflers

Boiler and Furnace Conversion:Servicing a Conversion Gas Burner

Systems, States, and Processes:Temperature and the Zeroth Law

Hydronic Heating Systems:Forced-Hot-Water Heating Systems

HEATING CIRCUITS:HIGH-EFFICIENCY FURNACES

Ducts and Duct Systems:Duct Heat Loss and Gain

The Second Law of Thermodynamics:Entropy as Property and The Gibbs Equation.