Cascade computational analysis
Rather than use cascade tests or correlations, computational methods are regularly applied to deter- mine blade loading, surface velocity distributions, losses, and deviation. This section briefly out- lines the key aspects of computational methods used for blade section analysis and some of the results they can produce. Further consideration of computational methods is presented in Chapter 6, including some presentation of three-dimensional CFD. However, it should be emphasized that the intention in this book is only to provide a general understanding of the capability of such methods and how they are used in turbomachinery design and analysis. Good references for further details are Stow (1989) and Denton and Dawes (1999).
Calculation geometry
Computational methods that perform the role of a cascade test are known as “blade-to-blade methods” since they compute the flow-field between adjacent blade sections on an unwrapped meridional-tangential (m-rθ) streamsurface.4 As discussed in Section 3.3, for cascade testing, the streamtube thickness does not necessarily remain constant through the blade passages and most modern blade-to-blade methods can accommodate an AVDR that is not equal to unity. Such methods are often referred to as quasi-three-dimensional (Q3D) since they are accounting for the 3D effects of streamtube divergence or convergence.
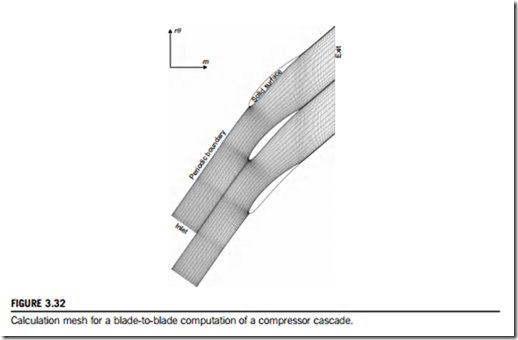
A typical computational mesh for a blade-to-blade method is shown in Figure 3.32. Note that in this case the mesh is for an inviscid calculation that does not resolve the boundary layers on the blade surfaces. The exact form of the mesh depends on the type of method used and the resolution required. Some meshes have regular, rectangular topology with fairly constant cell size, as in the case shown, whereas there are also methods that use triangular meshes with huge variations in cell size. In all cases, the mesh is only one cell thick and it represents a streamtube, so there can be no flow perpendicular to the plane of the mesh (into or out of the page).
Method types
The main task of a computational method is to determine, for each cell within a mesh, the flow properties that are compatible with the boundary conditions. Different numerical solvers take differ- ent approaches and include varying assumptions and simplifications. However, they are, in general, simply applying the fundamental laws of continuity, the steady flow energy equation, conservation of momentum, and the second law of thermodynamics, as presented in Chapter 1.
A technique known as a panel (or vortex) method assumes two-dimensional incompressible, inviscid flow. The method places vortices at a series of points on the blade pressure and suction surfaces. The strengths of the vortices are set such that there is no flow into or out of the blade surfaces. The flow at any point in the blade passages is then the linear sum of the influence of all of the vortices. This type of method is fairly limited for turbomachinery use since it is only applicable to incompressible, inviscid flow with uniform inflow.
A potential flow method is applicable to isentropic flow through a cascade. It essentially solves a form of the compressible continuity equation on a mesh, subject to constant stagnation enthalpy, isentropic relations, and the requirement for flow to leave a blade section trailing edge smoothly. They can be used for compressible flow cases provided there are no strong shock waves, but they cannot give any indication of blade losses. Potential flow methods such as Whitehead and Newton (1985) are still in use today to design turbine blade sections because they are very fast and the neglected viscous effects are usually small.
An Euler method treats each cell in a computational mesh as a control volume. It iteratively solves the equations for conservation of mass, momentum, and energy for each of these control volumes. A large number of iterations can be required to reach a converged, steady solution, which increases the run time, but typically Euler methods only take a minute or so on a modern computer. An Euler method can be used for compressible flow, but it does not include viscous effects. To account for boundary layers, a Navier-Stokes method can be used, which includes viscous terms in the momentum equation. Alternatively a coupled inviscid method and boundary layer solver can be used. In this, an Euler, or similar method, is used for the inviscid mainstream flow and a bound- ary layer solver is used to compute the development of the viscous boundary layers on the blade surface. Information is shared between these computations to account for the blockage of the boundary layer and the effects of the mainstream flow pressure distribution on the boundary layer parameters. A coupled method that is widely used today for blade section analysis and design is described in Giles and Drela (1987).
Note that many of the above methods can work in an “inverse” (or “design”) mode as well as the standard “analysis” mode. In analysis mode, the geometry is fixed, analogous to a cascade test. In the inverse mode, the user prescribes a surface velocity distribution, which the code then aims to achieve by manipulating the blade section geometry.
Boundary conditions
Figure 3.32 indicates the different types of domain boundary in a blade-to-blade computation. A fundamental assumption for a cascade is that the flow is the same in all blade passages. Therefore, all flow properties should repeat along the periodic boundaries and this can be pre- scribed as a boundary condition. On solid blade surfaces, there can be no flow into or out of the surface and thus the velocity normal to any surface is zero and this is specified as another boundary condition.
The inlet and exit boundary conditions are specified to match the required cascade operating point. As discussed in Section 3.3, the performance of a cascade can be expressed by functional relationships of the form
The boundary conditions must therefore be sufficient to fix the Mach number, inlet flow angle, and Reynolds number. For incompressible methods, the Mach number is irrelevant, and for inviscid (or isentropic) methods, the Reynolds number can also be omitted. Hence, there are fewer boundary conditions required for potential flow and panel methods.
In Euler and Navier-Stokes methods, the inlet stagnation pressure p01, the inlet stagnation temperature T01, and the inlet angle α1 are usually specified, along with the exit static pressure p2.
This is equivalent to how a cascade experiment is set up (see Figure 3.1): the inlet conditions p01 and T01 are set by the wind tunnel fan, the inlet angle α1 is set by the angle between the cascade axis and the test section, and the exit static pressure is fixed by the ambient pressure downstream of the cascade. If viscous effects are modeled, the Reynolds number is also set, either directly, or by specifying the fluid viscosity and the geometry scale.
Transonic effects
Euler methods and Navier-Stokes methods can handle transonic flow and strong shock waves, although the accuracy of their predictions is limited by the resolution of the computational mesh.
A shock wave will tend to be “smeared out” over a number of cells and the associated aerodynamic effects will not be accurately resolved. Figure 3.33 shows Mach number contours for a coupled inviscid method and boundary layer solver applied to a C4 compressor cascade operating with an inlet Mach number of 0.8 (This is the same condition and geometry as used in the surface Mach number plot in Figure 3.18). The figure shows a shock wave clearly captured on the blade suction surface. It also indicates the streamlines at the edge of the blade boundary layers that form the blade wake. This shows how in compressor blades the viscous effects can create significant blockage, which leads to an effect on the inviscid flow-field.
Viscous effects
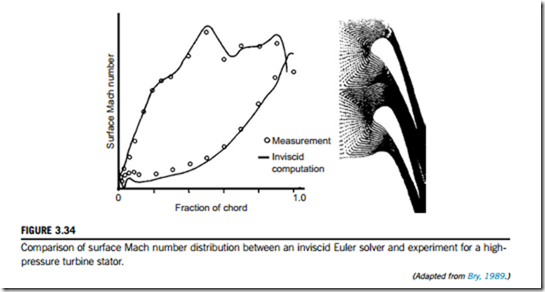
Inviscid methods cannot give an estimation of losses, but they can still be useful as they will calculate the blade surface velocity distribution, the blade loading and the diffusion levels on the surfaces. As discussed in Section 3.5, the state of the boundary layers and blade losses correlate with local diffusion levels. Inviscid methods can therefore be used to determine whether acceptable diffusion levels are maintained and what operating points lead to high diffusion. Figure 3.34 shows an example comparison between measured and computed surface velocity distributions around a turbine stator for a quasi-three-dimensional Euler method.
Methods that model viscous effects do not necessarily determine them accurately. There are several complex physical phenomena that may need to be modeled in the blade boundary layers such as laminar flow, transition to turbulence, turbulent flow, separation, and reattachment. A Navier-Stokes method requires models for turbulence and transition as well as a large number of mesh points close to any surfaces to resolve the flow gradients in the boundary layers. Denton and Dawes (1999) state that at high Reynolds number a Navier-Stokes solution should predict viscous losses accurate to within 10%, but at lower, transitional, Reynolds numbers the losses may be in error by 50%. In this case, a coupled inviscid and boundary layer method is more accurate and can provide a more detailed prediction of the boundary layer parameters. In applications where there are significant Reynolds number and transitional effects, such as low-pressure turbines for jet engines, coupled inviscid and boundary layer solvers have been shown to be accurate in reproducing cascade test results, see Stow (1989).
In all cases, a computational method user should be careful to ensure that all the relevant physics are sufficiently reproduced in their solver, that the method has been adequately calibrated, and that it has been applied correctly using a suitable mesh and appropriate boundary conditions.
It should then be possible to quickly generate useful cascade results (e.g., in the form shown in Figure 3.14 or 3.25) with a known level of accuracy.