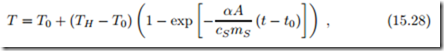Heating of a House
As first example for transient processes in open systems, we study the heating of a house in a simplified model. The house of volume V0 is initially in equilibrium with the outside environment at p0, T0. To elevate the temperature in the house to a pleasant value TH , the house is heated at constant rate Q˙ heat. Heat transfer through the walls leads to heat loss Q˙ loss to the outside. Moreover, the house exchanges air through gaps in doors, windows and walls, and we assume that the pressure stays constant at all times. We ask for the amount of heat that must be supplied to keep the house at the inside temperature TH , and for the time required to heat the house to that temperature.
The house consists of the mass mS of structural material (wood, stone, concrete, plaster, … ), which has the average specific heat cS . To simplify the calculation, we shall assume that the whole structure is at the temperature T (t), that is we ignore any inhomogeneous temperature distribution in the outside walls, which, in reality, would be colder further outside. The mass of air in the house is denoted as m˙ A (t) and is subject to change due to inflow or outflow through gaps.
The mass and energy balances for the house read
where α is the heat transfer coefficient for the house, U is the total internal energy (air and structure) and A is the outside surface. Kinetic and potential energies are ignored, and the house and air have the homogeneous temperature T . The last term in the energy balance, m˙ AhA, is the convective outflow of energy. As long as the house is heated, we expect only outflow, due to isobaric expansion of the inside air. In cooling of the house, say at night when the heating is switched off, the air contracts, and outside air (at h0) flows in.
Before we consider the time dependent process, we have a look at the final steady state, for which![]() and T = TH , so that the final house temperature is obtained as
and T = TH , so that the final house temperature is obtained as
This relation shows that the house temperature is controlled through adjustment of the heating rate Q˙ heat. Improved insulation reduces the heat transfer coefficient α and thus the heat requirement Q˙ heat.
With suitable choice of the energy constants, the internal energy of the house and the enthalpy of the air are
where cv and cp = cv +R are the specific heats of air, assumed to be constant. The mass of air in the house follows from the ideal gas law as
Combining the above, including eliminating the air mass by means of (15.23), yields a differential equation for temperature, which after some simplifications reads
where mH = p0 V0 is the final mass of air in the house. This equation describes the evolution of the inside temperature T towards TH over time t, in an implicit way. The first term on the left hand side describes the heating of the air, and the second term describes the heating of the structure.
We consider a small house with a footprint of 10 m × 10 m, a height of 3 m and a flat roof. The air volume of the house is approximately 300 m3 which at final conditions (TH , p0) corresponds to a mass of mH = p0 V0 = 350 kg.
Clearly, this mass, and the corresponding heat capacity mH cp, is much less than mass mS and heat capacity mS cS of the structure.
If we completely ignore the contribution to air heating, we obtain for the temperature an exponential relation,
where we have used (15.21).
In a house, normally first the air is heated, e.g., by radiators or forced air heating, and then heat is transferred from the warm air to the structure. If heat transfer to the structure is slow, the structure heating can be ignored, and the air temperature approaches the final temperature according to
where α now is the heat transfer coefficient between inside air (at T ) and structure (at T0).
The approach to the final temperature is determined by the time constants cpmA , respectively. Due to the large differences in mass between air and structure, the air heats up much faster than the structure.