Counter-Flow Heat Exchangers
Now we consider counter-flow heat exchangers (lower sign). The known inflow conditions are the temperatures TA (0) and TB (L), for which we find from (15.6)
This solution becomes singular for the special case αˆA = αˆB = αˆ. L’Hˆopital’s rule must be used to find the temperature curves for this case as
Thus, in general, we will observe exponential curves for the temperatures, but straight lines in the case that αˆA = αˆB . Figure 15.4 shows the temperature curves for three cases with different or equal values of αˆA and αˆB .
In particular we note that the exit temperatures are not limited by a common mean value as for co-flow exchange, but can be quite close to the inlet temperature of the other stream. For an exchanger of length L, the exit temperatures of the two streams are
Thus, stream A exits in equilibrium with stream B at x = L∞, but stream B cannot achieve equilibrium with the incoming stream A at x = 0. When αˆB > αˆ, the behavior is opposite. The only case where both exiting streams are in equilibrium with the incoming streams, in the case L → ∞, is for αˆB = αˆA = αˆ.
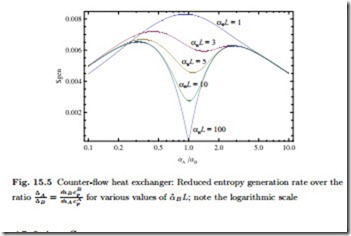
The above discussion already gives indication that a counter-flow heat exchanger works particularly well when αˆB = αˆA = αˆ, which is the case when the mass flows are matched such that m˙ AcA = m˙ B cB , see (15.5). The discussion of the entropy generation rate of the heat exchanger sheds more light on this. Again ignoring heat loss to the exterior, the entropy generation is