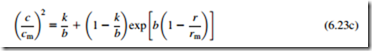The direct problem
The flow angle variation is specified in the direct problem and the radial equilibrium equation enables the solution of cx and cθ to be found.
The radial equilibrium equation is
2. If the flow angle α is made constant, then the above equation simplifies to
The vortex distribution represented by Eq. (6.22) is often employed in practice as untwisted blades are much simpler to manufacture.
The general solution of the radial equilibrium equation
A more general case applies when h0 5 h0ðrÞ; α 5 αðrÞ; and s 5 a constant. This specification gives the designer a much wider choice. A solution can be contrived as follows. From Eq. (6.20b), i.e.,
If the variation of α is specified by bðr=rmÞ 5 2 sin2 α, where b is a constant, it can be shown that
where k is a constant of integration.
These sort of analyses can be used in the preliminary design of blading and some computational methods use them to prescribe their boundary conditions, see Lakshminarayana (1996).