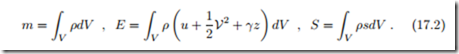Equilibrium in Isolated Systems
An isolated system does not exchange energy or mass with its surroundings. Accordingly, first and second law reduce to
with a constant mass m in the system. Since no work is exchanged, the volume V must be constant as well. According to the second law, the state of the system will change until the entropy has reached a maximum. However, since mass and energy of the system do not change over time, at all times the process is restricted by having the initial mass and energy enclosed in the system. The approach to equilibrium is a reorganization of the local properties of the system towards the final equilibrium state.
We study the approach to equilibrium for a single phase system; heterogeneous systems will be discussed later, in Sec. 17.7. For this we have to consider the total mass, energy and entropy by integration over the full system,
In order to avoid confusion with the Gibbs free energy, the gravitational acceleration is denoted by γ. Here, ρ, T , V, and u (ρ, T ), s (ρ, T ) are the local values of the thermodynamic properties, that is, ρ = ρ (−→r ), T = T (−→r ) etc., where −→r is the location in the volume V of the system, see Sec. 2.7.
Before we proceed, we need to state the momentum vector −M→ of the system.
Typically, we are interested in systems that are globally at rest, where the overall momentum vanishes, but we might consider also systems moving with a constant velocity −→v , so that −M→ = m−→v . Since all elements of the system have their own velocity −→ (−→r ), we find the total momentum by summing over the system,
here −→ is the local velocity vector with V = IAs long as no forces act on the system, its momentum will be constant; total momentum vanishes for a system at rest in the observer frame, −M→ = 0.
The equilibrium state is the maximum of entropy S under the constraints of given mass m, momentum −M→, and energy E. The best way to account for the constraints is the use of Lagrange multipliers Λρ, −→Λ M incorporate the constraints and maximize not S but
We proceed with evaluating these three conditions to find the equilibrium state. For convenience, we begin with the middle equation, (17.8), which gives immediately that the velocity is homogeneous in equilibrium,
where g is the Gibbs free energy, and γ is gravitational acceleration. With the temperature homogeneous, and the constant Lagrange multiplier Λρ, this is an implicit equation for the equilibrium density, which appears as an argument in the Gibbs free energy g (ρ, T ), or, alternatively, it is an equation for pressure p, if we write g (p, T ). Often we consider systems in which the potential energy can be ignored. For such systems, the Gibbs free energy is homogeneous, g (ρ, T ) = −T Λρ. Homogeneous Gibbs free energy and temperature implies that density and pressure are homogeneous as well. Phase In summary, maximizing entropy in the isolated system yields that the sys- tem is fully at rest, V = 0, has homogeneous temperature, T = 1/ΛE , and, in the gravitational field, has inhomogeneous density and pressure, given implicitly by g (T, ρ) = −T Λρ − γz. What remains is to determine the Lagrange multipliers ΛE = 1/T and Λρ, which follow from the given values of mass