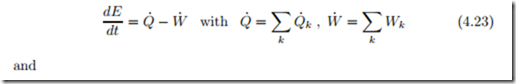The Entropy Balance
In the previous sections, we considered homogeneous systems that undergo equilibrium processes. To generalize for processes in inhomogeneous systems, we consider the system as a compound of sufficiently small subsystems. The key assumption is that each of the subsystems is in local equilibrium, so that it can be characterized by the same state properties as a macroscopic equilibrium system. To simplify the proceedings somewhat, we consider numbered subsystems of finite size, and summation. A more refined argument would consider infinitesimal cells dV , and integration.
Figure 4.3 indicates the splitting into subsystems, and highlights a sub- system i inside the system and a subsystem k at the system boundary. Temperature and pressure in the subsystems are given by Ti, pi and Tk, pk , respectively. Generally, temperature and pressure are inhomogeneous, that is adjacent subsystems have different temperatures and pressures. Accordingly, each subsystem interacts with its neighborhood through heat and work transfer as indicated by the arrows. Heat and work exchanged with the surroundings of the system are indicated as Q˙ k and W˙ k .
Internal energy and entropy in a subsystem i are denoted as Ei and Si, and, since both are extensive, the corresponding quantities for the complete system are obtained by summation over all subsystems, E = ),i Ei, S = ),i Si. Note that in the limit of infinitesimal subsystems the sums become integrals, as in Sec. 2.7. The balances of energy and entropy for a subsystem i read
where Q˙ i = ), Q˙ i,j is the net heat exchange, and W˙ i = ), W˙ i,j is the net work exchange for the subsystem. Here, the summation over j indicates the exchange of heat and work with the neighboring cells, such that, e.g., Q˙ i,j is the heat that i receives from the neighboring cell j.
To obtain first and second law for the compound system, we have to sum the corresponding laws for the subsystems, which gives
In the above Q˙ k is the heat transferred over a system boundary which has temperature Tk . As will be explained next, the summation over k concerns only heat and work exchange with the surroundings.
Since energy is conserved, the internal exchange of heat and work between subsystems cancels in the conservation law for energy (4.23). For instance, in the exchange between neighboring subsystems i and j, Qi,j is the heat that i receives from j and Wi,j is the work that i does on j. Moreover, Qj,i is the heat that j receives from i and Wj,i is the work that j does on i. Since energy is conserved, no energy is added or lost in transfer between I and j, that is Qi,j = −Qj,i and Wi,j = −Wj,i. Accordingly, the sums vanish, Qi,j +Qj,i = 0 and Wi,j +Wj,i = 0. Extension of the argument shows that the internal exchange of heat and work between subsystems adds up to zero, so that only exchange with the surroundings, indicated by subscript k, appears in (4.23).
Entropy, however, is not conserved, but may be produced. Exchange of heat and work between subsystems, if irreversible, will contribute to the entropy generation rate S˙gen. Thus, the total entropy generation rate S˙gen of the compound system is the sum of the entropy generation rates in the sub- systems S˙gen,i plus additional terms related to the energy transfer between subsystems, S˙gen = ),i S˙gen,i + ), Ti . In simple substances, entropy generation occurs due to internal heat flow and internal friction. We repeat that entropy generation is strictly positive, S˙gen > 0, in irreversible processes, and is zero, S˙gen = 0, in reversible processes.
To fully quantify entropy generation, that is to compute its actual value, requires the detailed local computation of all processes inside the system from the conservation laws and the second law as partial differential equations. The derivation and analysis of the local laws is a topic of Non-equilibrium Thermodynamics.
The above derivation of the second law equation (4.24) relies on the assumption that the equilibrium property relations for entropy are valid locally also for non-equilibrium systems. This local equilibrium hypothesis— equilibrium in a subsystem, but not in the compound system—works well for most systems in technical thermodynamics. It should be noted that the assumption breaks down for extremely strong non-equilibria; this lies outside the scope of our endeavours.