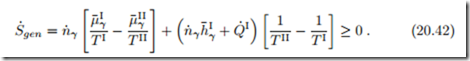The Chemical Potential as Driving Force for Mass Transfer
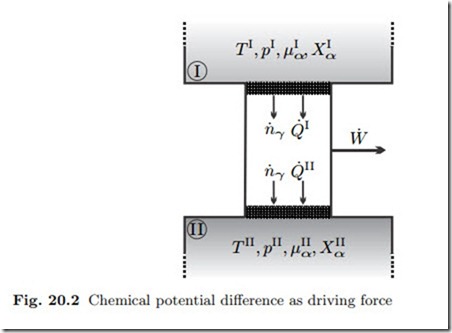
We consider the set-up shown in Fig. 20.2: Two reservoirs I and II contain mixtures of different temperature T , pressure p, and composition Xα, which remain constant at all times. Through semipermeable membranes the two reservoirs are connected to a heat and mass conducting duct. Due to the non-equilibrium between the two reservoirs we expect flows of mass and heat. The duct might contain devices to extract work from these flows.
The membranes let only component γ pass and we consider only steady state processes. Since only component γ passes through membranes and duct, the first and second law for the duct read
The right hand side of this equation vanishes in the case of thermal and chemical equilibrium, where T I = T II and μI = μII.
Power can be generated from the differences in temperature and chemical potential. We have studied heat engines, which are driven by temperature differences, in great detail in previous chapters. The generation of power from differences in the chemical potential, known as osmotic power generation, will be discussed further below. The maximum possible power is generated when transfer through the duct occurs fully reversibly, so that S˙gen = 0.
When the duct is fully irreversible, so that no power is generated, W˙ the amount of entropy produced (which must be non-negative) is
As before, in Sec. 4.10, we interpret the entropy generation in terms of thermodynamic forces and fluxes. The forces are the differences in reduced chemical potential, r μ¯ , and inverse temperature, r − , between the reservoirs. The related fluxes are the matter flow n˙ γ and the total energy flow ( hI + Q˙ I. Previously, when we discussed Newton’s law of cooling, we had only one flux-force pair, and set the flux proportional to the force. For the present setting, we have two such pairs, which offers a richer set of transport laws. Indeed, we allow for both forces to affect both fluxes, and write fluxes and forces as vectors, with a matrix of coefficients αij ,
As always, we made the transfer surface A explicit. To ensure positive entropy generation, the matrix of transport coefficients αij must be positive definite, which is the case for α11 > 0 and α11α22 − α12α21 > 0.
We note that transfer of matter does not only occur due to differences in pressure (typical flow), and composition (diffusion), but also in response to a temperature gradient (thermodiffusion, or Soret effect, Charles Soret 1854- 1904) ). Heat transfer does not only occur due to a temperature difference, but also due to differences in pressure or composition (Dufour effect, Louis Dufour 1832-1892).
A deep discussion of laws of this type reveals the Onsager reciprocity relations (Lars Onsager, 1903-1976), which for this case state that the matrix must be symmetric, α21 = α21. Careful experiments show that the so-called cross effects, which are described by the off-diagonal terms in the matrix, are less important than the direct effects, which are described by the diagonal terms. In engineering applications the cross effects are often ignored.1
When the flow n˙ γ goes from I to II as shown, the reduced chemical potential T I must be larger than T II . In other words, a difference in chemical potential causes a flow against the gradient of the (reduced) chemical potential.
When we ignore temperature differences (T I = T II = T ), we can expect a linear law of the form where κ = α11/T is a positive constitutive coefficient, and A is the cross section of the duct.
In the special case when both mixtures are ideal, and have the same pressures and temperatures, we have μ¯I − μ¯II = R¯T ln Xγ : there will be a particle flux unless both mole fractions are equilibrated.
In short, the desire to equilibrate the chemical potential leads to a flux of that component that can pass the duct. The flux direction is against the gradient, which reduces the gradient. According to Eq. (20.41), this flux can be used to produce power W˙ > 0. Inversion of the flux, that is forcing flow in the direction of the gradient, requires power input, W˙ < 0. This is fully equivalent to what we have seen on temperature differences: Heat will flow from hot to cold—against the gradient—by itself, and this heat flux can be used to produce power in a heat engine. Transferring heat from cold to hot—in the direction of the gradient—requires work input, i.e., a heat pump.