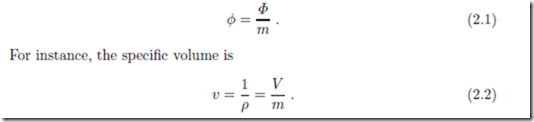Systems, States, and Processes
The Closed System
The first step in any thermodynamic consideration is to identify the system that one wishes to describe. Any complex system, e.g., a power plant, can be seen as a compound of some—or many—smaller and simpler systems that interact with each other. For the basic understanding of the thermodynamic laws it is best to begin with the simplest system, and study more complex systems later as assemblies of these simple systems.
The simplest system of interest is the closed system where a substance is enclosed by walls, and no mass flows over the system boundaries. The prototype of the closed system is a piston-cylinder device, as depicted in Fig. 2.1. We shall assume that the device contains a fixed amount of a simple substance, that is a substance that does not undergo chemical changes.
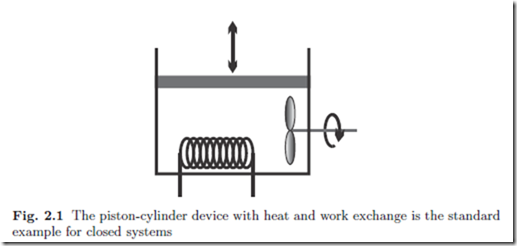There is only a small number of manipulations possible to change the state of a closed system, which are indicated in the figure: the volume of the system can be changed by moving the piston, the system can be stirred with a propeller, and the system can be heated or cooled by changing the temperature of the system boundary, as indicated by the heating coil.1 These actions lead to exchange of energy between the system and its surroundings, either by work in case of piston movement and stirring, or by the exchange of heat. The transfer of energy by work and heat will be formulated in the First Law of Thermodynamics.
The change of energy and volume of the system will lead to changes in other properties of the enclosed substance, in particular pressure and temperature. Thermodynamic laws and property relations are required to predict the changes of the different properties, and the exchange of heat and work.
Most processes have a direction in time. For instance, we can do work to move the propeller and stir a liquid, which increases the liquid temperature due to friction, but we will never observe that a liquid at rest suddenly begins to move a propeller and does work (e.g. the lifting of a weight), see Fig. 2.2. The direction of processes is formulated in the Second Law of Thermodynamics, which has, as will be seen, far ranging consequences for technical applications.
We shall first consider the complete set of thermodynamic equations for closed systems. In open systems mass crosses the system boundaries, and this leads to additional terms in the thermodynamic laws. These will be discussed in Chapter 9.
Micro and Macro
A macroscopic amount of matter filling the volume V , say a steel rod or a gas in a box, consists of an extremely large number—to the order of 1023— of atoms or molecules. These are in constant interaction which each other
1 Another possibility to heat or cool the system is through absorption and emission of radiation, and transfer of radiation across the system boundary.
and exchange energy and momentum, e.g., a gas particle in air at standard conditions undergoes about 109 collisions per second.
From the viewpoint of mechanics, one would have to describe each particle by its own (quantum mechanical) equation of motion, in which the interactions with all other particles would have to be taken into account. Obviously, due to the huge number of particles, this is not feasible. Fortunately, the constant in- teraction between particles leads to a collective behavior of the matter already in very small volume elements dV , in which the state of the matter can be de- scribed by few macroscopic properties like pressure, mass density, temperature and others. This allows us to describe the matter not as an assembly of atoms, but as a continuum where the state in each volume element dV is described by these few macroscopic properties.
Note that the underlying assumption is that the volume element contains a sufficiently large number of particles. Indeed, the continuum hypothesis reaks down under certain circumstances, in particular for highly rarefied gases. In all what follows, however, we shall only consider systems in which the assumption is well justified.
Mechanical State Properties
Of the many state properties that we shall meet, we first introduce those properties that can be easily measured, and are familiar from mechanics.
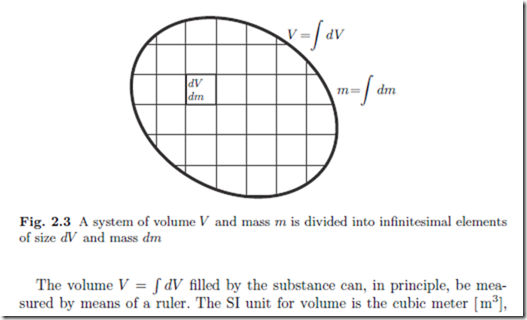
We consider a system of volume V which is filled by a mass m of substance. To describe variation of properties in space, it is useful to divide the system into infinitesimal elements of size dV and mass dm, as sketched in Fig. 2.3.
for smaller volumes one might use the litre, 1 litre = 10−3 m3, or the cubic centimetre, 1 cm3 = 10−3 litre = 10−6 m3.
The mass m = ( dm of the substance can be measured using a scale. The SI unit of mass is kilogram [ kg]. For small masses it is convenient to use the gram, 1 g = 10−3 kg, and for large masses it is convenient to use the metric ton, 1 t = 1000 kg.
The pressure p of the substance can be measured as the force required to keep a piston in place, divided by the surface area of the piston. The SI unit
Extensive and Intensive Properties
It is useful to distinguish between extensive properties, which are related to the size of the system, and intensive properties, which are independent of the size of the system. Mass m and volume V are extensive quantities, e.g., they double when the system is doubled; pressure p and temperature T are intensive properties, they remain unchanged when the system is doubled. As an example Fig. 2.4 shows the combination (or splitting) of a system at pressure p and temperature T , with total mass m1 + m2 and volume V1 + V2.
Specific Properties
A particular class of intensive properties are the specific properties, which are defined as the ratio between an extensive property and the correspond- ing mass. In general notation, the specific property φ corresponding to the extensive property Φ is defined as
Molar Properties
For the thermodynamic discussion of mixtures, reacting or not, it is advantageous to consider the number of particles involved rather than mass. The number of atoms or molecules is rather large and thus it is customary to count the number of particles in moles, with the unit [ mol] or [ kmol]. One mole is the number of atoms in 12 g of the carbon isotope 12C, which is given by the Avogadro constant (Amedeo Avogadro, 1776-1856)
Inhomogeneous States
In inhomogeneous states intensive and specific properties vary locally, that is they have different values in different volume elements dV . In this case, the local specific properties are defined through the values of the extensive property dΦ and the mass dm in the volume element,
Processes and Equilibrium States
A process is any change in one or more properties occurring within a system. The system depicted in Fig. 2.1 can be manipulated by moving the piston or propeller, and by exchanging heat. Any manipulation changes the state of the system locally and globally: a process occurs.
After all manipulation stops, the states in the volume elements will keep changing for a while—that is the process continues—until a stable final state is assumed. This stable final state is called the equilibrium state. The system will remain in the equilibrium state until a new manipulation commences.
Simple examples from daily life are: (a) A cup of coffee is stirred with a spoon. After the spoon is removed, the coffee will keep moving for a while until it comes to rest. It will stay at rest indefinitely, unless stirring is recommenced or the cup is moved. (b) Milk is poured into coffee. Initially, there are light-brown regions of large milk content and dark-brown regions of low milk content. After a while, however, coffee and milk are well-mixed, at midbrown color, and remain in that state. Stirring speeds the process up, but the mixing occurs also when no stirring takes place. (c) A spoon used to stir hot coffee becomes hot at the end immersed in the coffee. A while after it is removed from the cup, it will have assumed a homogeneous temperature. (d) Oil mixed with vinegar by stirring will separate after a while, with oil on top of the vinegar. The last example shows that not all equilibrium states are homogeneous; however, temperature will always be homogeneous in equilibrium.
In short, observation of daily processes, and experiments in the laboratory, show that a system that is left to itself for a sufficiently long time will approach a stable equilibrium state, and will remain in this state as long as the system is not subjected to further action.
The details of the equilibrium state depend on the constraints on the system, in particular material, size and energy. The time required for reaching the equilibrium state depends on the initial deviation from the equilibrium state, the material, and the geometry.2 A change of pressure at the system boundary propagates with the speed of sound (sound is a pressure wave) into the system, which will reach a new equilibrium pressure relatively fast. On the other hand, a change of temperature at the system boundary diffuses relatively slowly into the system: the spoon that is used to stir hot coffee needs quite a while to feel hot at the side that is not immersed in the cup.
Quasi-static and Fast Processes
When one starts to manipulate a system that is initially in equilibrium, the equilibrium state is disturbed, and a new process occurs. When the manipulation happens sufficiently slow, the system can adapt so that it is in an equilibrium state at any time. Slow processes that lead the system through a series of equilibrium states are called quasi-static, or quasi-equilibrium, processes.
If the manipulation that causes a quasi-static process stops, the system is already in an equilibrium state, and no further change will be observed.
Equilibrium states are simple, quite often they are homogenous states, or can be approximated as homogeneous states. The state of the system is fully described by few extensive properties, such as mass, volume, energy, and the corresponding pressure and temperature.
When the manipulation is fast, so that the system has no time to reach a new equilibrium state, it will be in non-equilibrium states. If the manipulation that causes a non-equilibrium process stops, the system will undergo changes until it has reached its equilibrium state. The equilibration process takes place while no manipulation occurs, i.e., the system is left to itself. Thus, the equilibration is an uncontrolled process.
Non-equilibrium processes typically are inhomogeneous. Their proper description requires values of the properties at all locations −→r (i.e., in all volume elements dV ) of the system. The detailed description of non-equilibrium pro- cesses is more complex than the description of quasi-static processes.
All real-life applications of thermodynamics involve some degree of non- equilibrium. Quasi-static processes are an idealization that serves to approx- imate real-life—i.e., non-equilibrium—processes.
Reversible and Irreversible Processes
The approach to equilibrium introduces a timeline for processes: As time progresses, an isolated system will always go towards its unique equilibrium state. The opposite will not be observed, that is a system will never be seen spontaneously leaving its equilibrium state when no manipulation occurs.
Indeed, we immediately detect whether a movie of a non-equilibrium process is played forward or backwards: well mixed milk coffee will not separate suddenly into milk and coffee; a spoon of constant temperature will not suddenly become hot at one end, and cold at the other; a propeller immersed in a fluid at rest will not suddenly start to move and lift a weight (Fig. 2.2);
oil on top of water will not suddenly mix with the water; etc. We shall call processes with a time-line irreversible.
Only for quasi-static processes, where the system is always in equilibrium states, we cannot distinguish whether a movie is played forwards or back- wards. We shall call these processes reversible. Since equilibration requires time, quasi-static, or reversible, processes typically are slow processes, so that the system always has sufficient time to adapt to an imposed change.
Equilibration processes can have quite different time scales. For instance, pressure changes are transported with the speed of sound (∼ 350 m ), and piston cylinder systems can be approximated as quasi-static if the piston velocity is significantly below the speed of sound. The mean piston speed in a car engine, which depends on stroke and speed, is typically below 20 m , hence compression and expansion processes in a car engine can be considered as quasi-static. Heat transfer, on the other hand, is a very slow process, with a time scale determined by the heat conductivity. Accordingly, quasi-static processes involving heating must be rather slow. For fast processes such as the compression and expansion process in a car engine, there is no time at all for significant heat transfer between the cylinder walls and the gas, and the process can be approximated as quasi-static processes with no heating.
The second law of thermodynamics will be introduced as formalization of the observation that an isolated system is moving towards a unique equilibrium state, and will allow for a more formal definition of reversible and irreversible processes.