Semi-perfect gas:
It can be observed that from the definition of cp and cv that the specific heats can be either constants or functions of temperature.
A semi-perfect gas is one which follows the ideal gas relation with its specific heats being functions of temperature.
For example the constant pressure molal specific heat of air at low pressure is related to the temperature by the empirical relation
Where cp is in kJ/kg-mole K and T is in Kelvin.
It can be seen that integration of specific heat equation is time consuming. Hence Keenan and Kaye developed the gas tables (Table C-21) to take into account the variation of specific heats with temperature. Internal energy and enthalpy of various gases including air at low pressure for wide range of temperature are tabulated in these tables. The table illustrates the properties of air taking into account the variation of specific heats with temperature.
Gas table may also be used for isentropic processes of perfect gases to relate properties by introducing a relative pressure pr and a relative volume vr.
The entropy at a reference state where the temperature is T0 and the pressure is 1 bar is assumed as zero. Therefore at a temperature T and pressure p, the entropy s is given by
The values of relative pressure pr and relative volume vr over a wide range of temperature are tabulated in gas tables.
Problems
1. 1.25 m3 of air at 1800C at 8 bar is undergoing a constant pressure until the volume is doubled.
Determine the change in the entropy and enthalpy of air.
2. 1kg of air initially at 270C is heated reversibly at constant pressure until the volume is doubled, and then is heated at constant volume until the pressure is doubled. For the total path find i) Work transfer, ii) Heat transfer, iii) Change in entropy
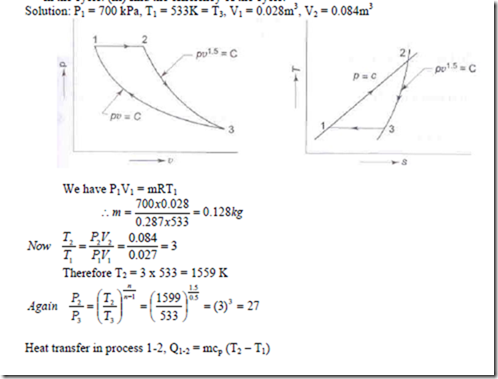
3. A mass of air is initially at 2600C and 700 kPa, and occupies 0.028m3. The air is expanded at constant pressure to 0.084m3. A polytropic process with n = 1.5 is then carried out, followed by a constant temperature process which completes a cycle. All the processes are reversible.
(i) sketch the cycle in the P-v and T-s diagrams. (ii) find the heat received and heat rejected in the cycle. (iii) find the efficiency of the cycle.
6. The cooking gas cylinder (mostly methane) is about 250mm in diameter and 800mm in height. It is charged to 12 MPa at room temperature of 270C. i) Assuming ideal gas law, find the mass of the gas filled in the cylinder, ii) If the cylinder is to be protected against excessive pressure by means of a fusible plug, at what temperature the plug has to melt to limit the maximum pressure to 15 MPa? Assume the molecular weight of methane to be 16kg/kg-mole.
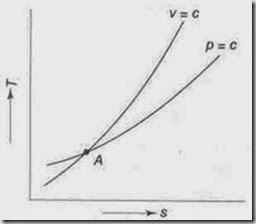
7. Show that for an ideal gas, the slope of the constant volume line on the T-s diagram is more than that of the constant pressure line.
i.e., the slope of the constant volume line passing through a point is steeper than that of the constant pressure line passing through same point.
8. A mass of 0.25 kg of an ideal gas has a pressure of 300 kPa, a temperature of 800C, and a volume of 0.07 m3. The gas undergoes an irreversible adiabatic process to a final pressure of 300 kPa and final volume of 0.1 m3 during which the work done on the gas is 25 kJ. Evaluate the cp and cv of the gas and increase in entropy of the gas.
1. An ideal gas cycle consisting of three processes uses Argon (M = 40) as a working substance.
Process 1-2 is a reversible adiabatic expansion from 0.014m3, 700 kPa, 2800C to 0.056m3. Process 2-3 is a reversible isothermal process and process 3-1 is a constant pressure process. Sketch the cycle on P-v and T-s diagrams and determine (i) work transfer in each of the three processes (ii) heat transfer in each of the three processes and (iii) net work output from the cycle. Assume for Argon g = 1.67.
10. A mass of an ideal gas exists initially at 200 kPa, 300K and 0.5 m3/ kg. The value of g is 1.4. (i)Determine the specific heats of the gas. (ii)What is the change in entropy when the gas is expanded to a pressure of 100 kPa according to the law pv1.3 = constant (iii) What will be the change in entropy if the process is according to the law pv1.5 = constant (iv) What inference you can draw from this example.
(iv) It can be seen from the results of (ii) and (iii) above that entropy increases when n < g and it decreases when n > g.
11. A closed rigid cylinder is divided by a diaphragm into two equal compartments, each of volume 0.1 m3. Each compartment contains air at a temperature of 200C. The pressure in one compartment is 2.5 MPa and in the other compartment it is 1 MPa. The diaphragm is ruptured so that the air in the compartments mix to bring the pressure to a uniform value through the insulated cylinder. Find the net change in entropy due to mixing process.
Solution: Let suffix 1 denote the condition of air in the left half of the cylinder, suffix 2 the conditions in the right half of the cylinder and suffix 3 the condition after mixing
12. 1 kg of air expands isentropically in a steady flow process from an initial state of 6.5 bar and 500 K to a final state of 1 bar. Neglecting kinetic and potential energies, assuming the air to be a semi perfect gas, compute the temperature of the air at the final state and work developed during the process.
Solution: From table C-21 (Thermodynamic Data Hand Book, by B.T. Nijaguna and B.S. Samaga) at T1 = 500 K Pr1 = 8.411 and h1 = 503.02 kJ/kg
13. Air is compressed from 1 bar, 270C to 4.5 bar, 1770C. Determine the change in entropy per kg of air (i) taking variation of specific heats into account and (ii) assuming specific heat at constant pressure to be constant and is equal to 1.01 kJ/kg-K over this range of temperature.
Thermodynamics of Non-reactive Mixtures
Assumptions:
1. Each individual constituent of the mixture behaves like a perfect gas.
2. The mixture behaves like a perfect gas.
3. Individual constituents do not react chemically when the mixture is undergoing a process.
Consider a mixture of gases a, b, c, …. existing in equilibrium at a pressure P, temperature T and having a volume V as shown in figure.
The total mass of the mixture is equal to the sum of the masses of the individual gases, i.e., mm = ma + mb + mc + …….. where subscript m = mixture, a, b, c = individual gases.
Mass fraction: The mass fraction of any component is defined as the ratio of the mass of that component to the total mass of the mixture. It is denoted by mf.
Where the subscript i stands for the ith component. It shows that the sum of the mass fraction of all components in a mixture is unity.
Mole fraction: If the analysis of a gas mixture is made on the basis of the number of moles of each component present, it is termed a molar analysis. The total number of moles for the mixture is equal to the sum of the number of moles of the individual gases
i.e., nm = na + nb + nc + …….. where subscript m = mixture, a, b, c = individual gases.
(A mole of a substance has a mass numerically equal to the molecular weight of the substance, i.e., 1 kg mol of O2 has a mass of 32 kg, 1 kg mol of N2 has a mass of 28 kg, etc.,)
The mole fraction of any component is defined as the ratio of the number of moles of that component to the total number of moles. It is denoted by y
i.e., the sum of the mole fraction of all components in a mixture is unity.
The mass of a substance m is equal to the product of the number of moles n and the molecular weight (molar mass) M, or m = nM
For each of the components we can write, nm Mm = na Ma + nb Mb + ncMc + ……
Where Mm is the average molar mass or molecular weight of the mixture. Or Mm = yaMa + ybMb + ycMc
Thus, the average molecular weight of a gas mixture is the sum of the products of all the components of the mole fraction and corresponding molecular weight of each component.
Partial pressure of a constituent in a mixture is the pressure exerted when it alone occupies the mixture volume at mixture temperature. If Pa is partial pressure of gas ‘a’, then PaV = maRaT Where ma = mass of gas ‘a’, Ra = gas constant for gas ‘a’, similarly PbV = mbRbT
Partial Volume: Partial volume of a gas in a mixture is the volume occupied by the gas component at mixture pressure and temperature. Let Va = partial volume of gas ‘a’ and Vb = partial volume of gas ‘b’
i.e., PVa = maRaT & PVb = mbRbT
The Gibbs-Dalton Law
Consider a mixture of gases, each component at the temperature of the mixture occupying the entire volume occupied by the mixture, and exerting only a fraction of the total pressure as shown in figure.
The above equation is known as the Gibbs Dalton Law of partial pressure, which states that the total pressure exerted by a mixture of gases is equal to the sum of the partial pressures of the individual components, if each component is considered to exist alone at the temperature and volume of the mixture.
Related posts:
Incoming search terms:
- semi perfect gas
- 1 kg of air is heated reversibly at constant pressure froman initial state of 300 k
- mass of air is initially at 260c 700kpa and 0 028 the air expand at constant pressure a polytropic proceds and isothermal
- perfect and semi perfect gas
- perfect and semi perfect gasses
- perfect gas & semi perfect gas
- Propert of semi perfect gas
- 0 25 kg of an ideal gases pressure of 300 kpa temerature of 80°c volume of 0 07 m3
- semi perfect gas inner energy
- semi-perfect gas definition
- what is perfect and semi perfect in ideal gas
- what is semi perfect gas
- formula del gas perfecto
- examples of semi gases
- example of semi gases
- 1 kg ideal gas in polytropic process find change in entropy
- A closed rigid cylinder is divided by a diaphargm into two equal compartements diaphargm ruptures find change in entropy
- A closed rigid cylinder is divided by a diaphragm into two equal compartment
- a closed rigid cylinder is divided by a diaphragm into two equal component each of volume 1m^3 each components contains air at atemp of 20degre celcius The pressure in one compartment is 2 5 mpa and in other compartment is 1 mpa
- a mass of 0 25 kg of an ideal gas has a pressure of 300 kPa a temperature of 80 degree celcius
- a mass of 0 25kg ideal gas at 300kpa
- efficiency of perfect gases
- entropy as a function of temperature and pressure
- entropy change after mixing of gases by rupturing of diaphragm
- example of semi gas
- what is semi perfect gases with example
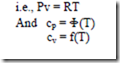


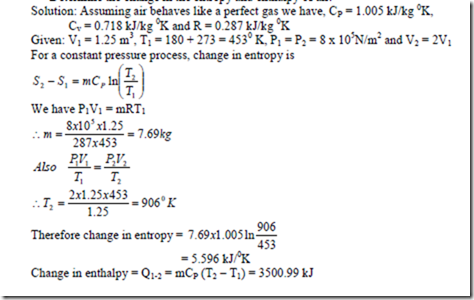





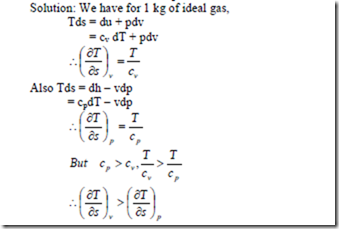

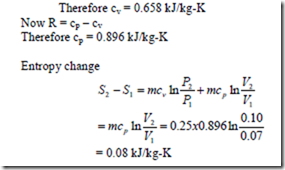
![image_thumb[1] image_thumb[1]](http://lh3.ggpht.com/-iQG-XwmT3zo/VONuhGOHHNI/AAAAAAABQmk/7htvVdu2b30/image_thumb%25255B1%25255D_thumb.png?imgmax=800)
![image_thumb[2] image_thumb[2]](http://lh3.ggpht.com/-ayKjGwHP9Ps/VONuly1E9ZI/AAAAAAABQm0/GuVdR--qhbA/image_thumb%25255B2%25255D_thumb.png?imgmax=800)
![image_thumb[3] image_thumb[3]](http://lh3.ggpht.com/-3Q7HUzttGy8/VONuokidZjI/AAAAAAABQnE/oZsUWXkt4wA/image_thumb%25255B3%25255D_thumb.png?imgmax=800)
![image_thumb[4] image_thumb[4]](http://lh3.ggpht.com/-Smd4VpZ6WTM/VONusgTt6GI/AAAAAAABQnU/_eSFXD7Hnyo/image_thumb%25255B4%25255D_thumb.png?imgmax=800)
![image_thumb[5] image_thumb[5]](http://lh6.ggpht.com/-x-WyMnvBZqc/VONuwfjlnhI/AAAAAAABQnk/WGrh_gb5z8w/image_thumb%25255B5%25255D_thumb.png?imgmax=800)
![image_thumb[6] image_thumb[6]](http://lh4.ggpht.com/-Mdef2D8pPxs/VONu0IQIiDI/AAAAAAABQn0/vZV9wyQvDis/image_thumb%25255B6%25255D_thumb.png?imgmax=800)
![image_thumb[7] image_thumb[7]](http://lh4.ggpht.com/-VtAs5pfbX5U/VONu38hNjUI/AAAAAAABQoE/hij3_GnEQs4/image_thumb%25255B7%25255D_thumb.png?imgmax=800)
![image_thumb[8] image_thumb[8]](http://lh5.ggpht.com/-k_KLoZ_qrJY/VONu7WIcmAI/AAAAAAABQoU/SYXND_Dsgg8/image_thumb%25255B8%25255D_thumb.png?imgmax=800)
![image_thumb[9] image_thumb[9]](http://lh6.ggpht.com/-SF9qHeUAFiQ/VONu-RrdT3I/AAAAAAABQok/no5HL3P8p8I/image_thumb%25255B9%25255D_thumb.png?imgmax=800)
![image_thumb[10] image_thumb[10]](http://lh4.ggpht.com/-Pju8VWGJgzg/VONvBDskFzI/AAAAAAABQo0/F8WSzEIk3aE/image_thumb%25255B10%25255D_thumb.png?imgmax=800)
![image_thumb[11] image_thumb[11]](http://lh5.ggpht.com/-CUfJfaD4QQg/VONvDpdHt7I/AAAAAAABQpE/V-hJ9MU7_sc/image_thumb%25255B11%25255D_thumb.png?imgmax=800)
![image_thumb[12] image_thumb[12]](http://lh3.ggpht.com/-vlmAPDliIqM/VONvHcvSEXI/AAAAAAABQpU/BCUCt1LUtEo/image_thumb%25255B12%25255D_thumb.png?imgmax=800)
![image_thumb[13] image_thumb[13]](http://lh6.ggpht.com/-RWvLO-8n4Hg/VONvKarReuI/AAAAAAABQpk/KFkTF9KrV9c/image_thumb%25255B13%25255D_thumb.png?imgmax=800)
![image_thumb[14] image_thumb[14]](http://lh5.ggpht.com/-7flzF_Nd054/VONvNPXp2RI/AAAAAAABQp0/iCxB5PYMyXI/image_thumb%25255B14%25255D_thumb.png?imgmax=800)