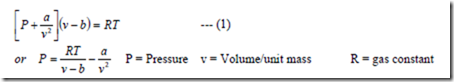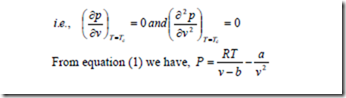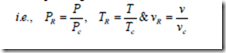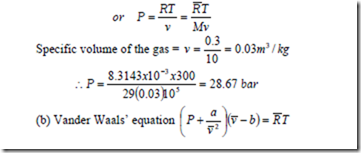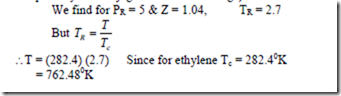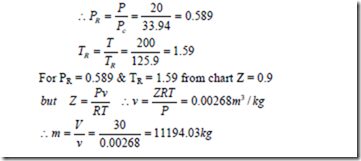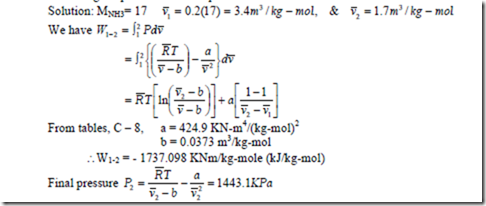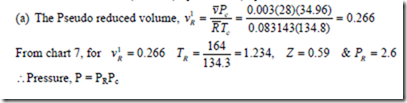Real Gases

Real Gases

Introduction

An ideal gas is a gas having no forces of intermolecular attraction. The gases which follow the gas laws at all range of pressures and temperatures are considered as ‘ideal gases’. An ideal gas obeys the perfect gas equation Pv = RT and has constant specific heat capacities.

A real gas is a gas having forces of inter molecular attraction. At very low pressure relative to the critical pressure or at very high temperatures relative to the critical temperature, real gases behave nearly the same way as a perfect gas. But since at high pressure or at low temperatures the deviation of real gases from the perfect gas relation is appreciable, these conditions must be observed carefully, otherwise errors are likely to result from inappropriate application of the perfect gas laws.

Due to these facts, numerous equations of state for real gas have been developed, the derivation of which is either analytical, based on the kinetic theory of gases, or empirical, derived from an experimental data.

Vander Waals’ Equation of State:

In deriving the equation of state for perfect gases it is assumed that the volume occupied by the molecules of the gas in comparison to the volume occupied by the gas and the force of attraction between the adjacent molecules is very small and hence the molecules of gas are neglected. At low pressures, where the mean free path is large compared to the size of the molecules, these assumptions are quite reasonable. But at high pressure, where the molecules come close to each other, these are far from correct. Vander waals’ equation introduces terms to take into account of these two modifying factors into the equation of state for a perfect gas.

The Vander Waals’ equation of state is given by,

where a and b are constants for any one gas, which can be determined experimentally, the constants account for the intermolecular attractions and finite size of the molecules which were assumed to be non-existent in an ideal gas. The term a/v² accounts for the intermolecular forces

i. force of cohesion and the term b was introduced to account for the volume occupied by the

molecules i.e., co-volume.

If the volume of one mole is considered, then the above equation can be written as,

Determination of Van der Waals constants in terms of critical properties

The determination of two constants a and b in the Van der Waals equation is based on the fact that the critical isotherm on a p-v diagram has a horizontal inflexion point at the critical point. Therefore the first and second derivative of P with respect v at the critical point must be zero.

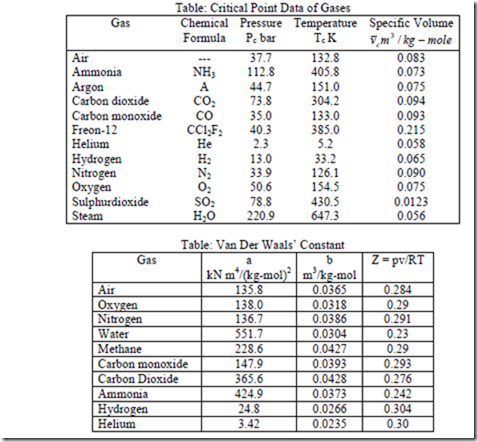
Note: Usually constants a and b for different gases are given.

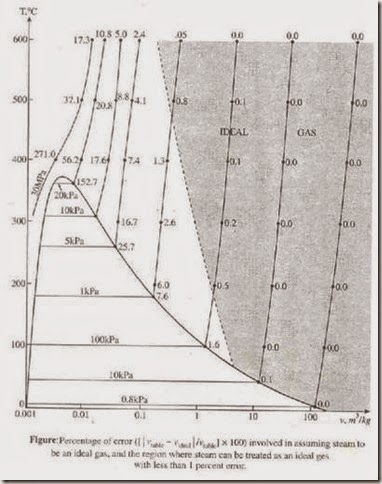
Compressibility Factor and Compressibility Chart:

The specific volume of a gas becomes very large when the pressure is low or temperature is high. Thus it is not possible to conveniently represent the behaviour of real gases at low pressure and high temperature.

For a perfect gas, the equation of state is Pv = RT. But, for a real gas, a correction factor has to be introduced in the perfect gas to take into account the deviation of the real gas from the perfect gas equation. This factor is known as the compressibility factor, Z and is defined as,

Z = Pv/RT

Z = 1 for a perfect gas. For real gases the value of Z is finite and it may be less or more than unity depending on the temperature and pressure of the gas.

Reduced Properties:

The real gases follow closely the ideal gas equation only at low pressures and high temperatures.

The pressures and temperatures depend on the critical pressure and critical temperature of the real gases. For example – 1000C is a low temperature for most of the gases, but not for air or nitrogen. Air or nitrogen can be treated as ideal gas at this temperature and atmospheric pressure with an error which is <1%. This is because nitrogen is well over its critical temperature of -1470C and away from the saturation region. At this temperature and pressure most of the substances would exist in solid phase. Hence, the pressure and temperature of a substance is high or low relative to its critical pressure or temperature.

Gases behave differently at a given pressure and temperature, but they behave very much the same at temperatures and pressures normalized with respect to their critical temperatures and pressures. The ratios of pressure, temperature and specific volume of a real gas to the corresponding critical values are called the reduced properties.

Law of Corresponding states:

This law is used in the approximate determination of the properties of real gases when their properties at the critical state are known. According to this law, there is a functional relationship for all substances, which may be expressed mathematically as vR = f (PR,TR). From this law it is clear that if any two gases have equal values of reduced pressure and reduced temperature, they will have the same value of reduced volume. This law is most accurate in the vicinity of the critical point.

Generalized Compressibility Chart:

The compressibility factor of any gas is a function of only two properties, usually temperature and pressure so that Z1 = f (TR, PR) except near the critical point. This is the basis for the generalized compressibility chart.

The generalized compressibility chart is plotted with Z versus PR for various values of TR. This is constructed by plotting the known data of one or more gases and can be used for any gas.

It may be seen from the chart that the value of the compressibility factor at the critical state is

about 0.25. Note that the value of Z obtained from Van der waals’ equation of state at the critical

The following observations can be made from the generalized compressibility chart:

At very low pressures (PR <<1), the gases behave as an ideal gas regardless of temperature.
At high temperature (TR > 2), ideal gas behaviour can be assumed with good accuracy regardless of pressure except when (PR >> 1).
The deviation of a gas from ideal gas behaviour is greatest in the vicinity of the critical point.

The compressibility factor can also be obtained from v-T or v-P data. Since the critical volume may not be consistent with the generalized chart, the pseudo critical specific volume vc1 is used in the definition of reduced volume. It is defined by v1 = RT / P . The pseudo reduced volume

Problems

1. A rigid vessel of volume 0.3 m3 contains 10 kg of air at 3000K. Using (a) the perfect gas equation, (b) the Vander Walls’ equation of state and (c) generalized compressibility chart, determine the pressure which would be exerted by the air on the vessel.

Solution: (a) The perfect gas equation is Pv = RT

3. If the values for the reduced pressure and compressibility factor for ethylene are 5 bar and 1.04 respectively, compute the temperature.

Solution: From generated computer chart (from chart 7 in thermodynamic Data Hand Book compiled by B.T. Nijaguna and B.S. Samaga)

4. Using the compressibility chart calculate (a) density of N2 at 260 bar & 150C. (b) What should be the temperature of 1.4 kg of CO2 gas in a container at a pressure of 200 bar to be have as an ideal gas.

Solution: For N2. from table C-6 (in thermodynamic Data Hand Book compiled by B.T. Nijaguna and B.S. Samaga) Tc = 125.90K Pc = 33.94

7. The specific volume of CO2 at 1200C is 1.2 m3/kg. Determine the pressure exerted by CO2 using Van der Waals’ equation. If CO2 is treated as an ideal gas, what should be the pressure exerted.

Ans: P = 61.8 KPa Pid = 61.88 KPa

8. One kg mol of NH3 undergoes a reversible non-flow isothermal compression process and the volume decreases from 0.2 m3/kg to 0.1 m3/kg, the initial temperature being 450C. If the gas obeys Van-der-waals’ equation during the compression process, determine the work done during the process and final pressure.

9. Determine the pressure of CO gas having volume of 0.003m3/kg at 164 K with the use of generalized computer chart. Also determine if the volume of gas is reduced to 80% of the initial volume, what is the temperature of the gas at the same pressure?