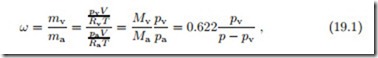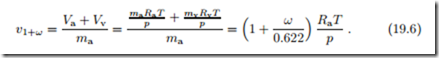Characterization of Moist Air
Psychros and metro are Greek words meaning cold and measure, respectively, and psychrometrics describes moist air: mixtures of air and water vapor with possibly some liquid water present as well. Psychrometrics is most important for designing proper air conditioning systems for buildings, where the air should be not too dry or moist, to make the environment comfortable; moreover, moisture buildup at (or in!) walls must be prevented.
This chapter describes how to characterize and analyze moist air mixtures, and discusses basic processes for moisturizing and dehumidification in HVAC systems (Heating-Ventilating-Air-Conditioning).
We consider air-vapor mixtures at temperature T and pressure p = pa +pv.
Air behaves as an ideal gas, hence the partial pressure of air, pa, follows the ideal gas law. At the relevant temperatures, the partial pressure of the vapor in moist air, pv , is so low that the vapor can be described as an ideal gas as well.
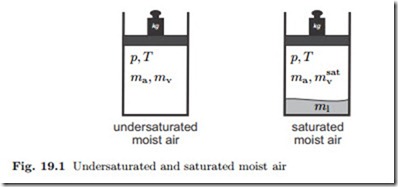
The vapor pressure cannot exceed the saturation pressure psat (T ). If pv < psat (T ) there is no liquid water present, but if pv = psat (T ) some liquid water will be present either in form of droplets (fog), or as an larger amount on the bottom. Figure 19.1 illustrates undersaturated moist air as a mixture of air and vapor, and saturated moist air as a mixture of air, vapor, and liquid water.
Since the saturation pressure psat (T ) increases with temperature, warm air can hold more water vapor than cold air. Cooling of moist air can lead to condensation of water, e.g., on cold bottles, or on eyeglasses when one enters the warm and humid air of a house coming in from a cold winter environment.
The humidity ratio ω, also known as specific humidity, is defined as the ratio of vapor and air mass in a sample of moist air of the volume V ,
where it was used that, for ideal gas mixtures, Xα = pα . Whether we perceive moist air as comfortable or not depends on the temperature and the relative humidity. In a dry environment, the human body loses a lot of moisture to evaporation from the skin and in breathing; one must drink a lot to replenish the moisture. In deserts, it helps to cover the body loosely with cloth, to prevent exposure of skin to the dry air, thus limiting evaporation from the skin. In high humidity, the air cannot accept more vapor, and thus sweat does not evaporate which results in difficulty to regulate the body temperature.
For buildings, a relative humidity of φ "’ 0.6 is providing the most pleasant environment.
The enthalpy of a moist air sample is H = Ha + Hv = maha + mv hv , (19.4) where ha (T ) and hv = hg (T ) are the specific enthalpies of air and water vapor. Since the amount of vapor changes due to evaporation and condensation, it is convenient to base the specific enthalpy of moist air on the dry air mass and we write1
Since at these low pressures air and vapor are ideal gases, their enthalpies depend only on temperature T , while the enthalpy of moist air, h1+ω , depends also on the humidity ratio ω.
The specific volume of moist air per unit mass of dry air can be computed from the Amagat model as, again with Mv = 0.622,
Dewpoint
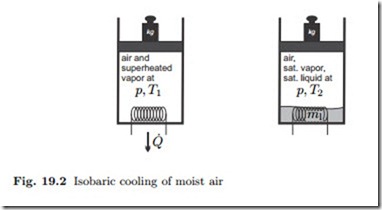
In isobaric cooling, see Fig. 19.2, the partial pressures of air and vapor stay constant as long as no water condenses. The dewpoint temperature Td is defined as the temperature at which vapor starts to condense when moist air is isobarically cooled,2
Figure 19.3 illustrates the cooling and condensation process for water in air in a T-s-diagram. Initially, the vapor is at state 1. No water condenses as the vapor is cooled until it reaches the dewpoint (state d). In the final state, the air is mixed with saturated vapor (state 2) and saturated liquid (state 3).