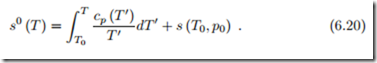The Ideal Gas
When the temperature of a vapor is sufficiently above the critical temperature or when the pressure is sufficiently below the critical pressure, it will obey the ideal gas law
where R = R¯/M is the gas constant. We have discussed ideal gases already in Sec. 2.15, and used the ideal gas law and the caloric equation of state in examples. We repeat some of the property relations and add new ones.
Experiments and theoretical considerations (see Sec. 16.3) show that for ideal gases internal energy u and enthalpy h = u + pv = u + RT depend on temperature only. Therefore, also their derivatives, the specific heats at constant volume, cv , and at constant pressure, cp, defined in (3.15, 3.22), depend only on temperature,
The constant of integration is chosen such that s0 (T ) is the ideal gas entropy at reference pressure p0 = 1 bar. The value of the reference entropy s (T0, p0) can be obtained from the third law, which will be discussed later (Sec. 23.6). As long as non-reacting mixtures are considered, its value is unimportant, since it cancels in all calculations. Indeed, only entropy differences are relevant, for which we find
In summary, energy and enthalpy of the ideal gas depend only on temperature, and its entropy depends explicitly on pressure (6.21) or volume (6.22), and on temperature through the function s0 (T ). The temperature dependent quantities u (T ) ,h (T ) , s0 (T ) are tabulated.3
As an example we consider a property table for air. The molar specific heat of air can be approximated by the Shomate equation
The mass based specific heats are cp = c¯p/M and cv = cp −R. Internal energy u, enthalpy h and entropy function s0 (T ) follow from integration using the formulas above. Figure 6.17 shows the resulting table.
Tables for other gases are widely available, or can be easily produced from the Shomate equation with the appropriate data for the coefficients, which can be found, e.g., from NIST (http://webbook.nist.gov/).