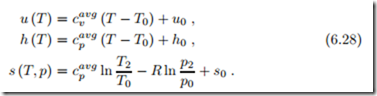Specific Heats and Cold Gas Approximation
The value of the specific heat is related to the degrees of freedom of a molecule. Specifically, each degree of freedom contributes 1 R to the specific heat at constant volume (equipartition of energy). The atoms of monatomic gases are essentially spheres that can translate in three directions (up/down, right/left, forward/backward); accordingly, the specific heat of monatomic gases is cv = 3 × 1 R.
For diatomic gases like oxygen (O2), nitrogen (N2), hydrogen (H2), the molecules are shaped like dumb-bells. At low temperatures these have, in addition to their three translational degrees of freedom, two rotational degrees of freedom for the rotation about two principal axes—there is no rotation around the longitudinal axis. More complex molecules like carbondioxid (CO2) and water (H2O) have three translational and three rotational degrees of freedom. Moreover, the molecules can oscillate, the more complicated a molecule is, the more oscillating modes are observed.
At sufficiently low temperatures only translational and rotational modes are excited. With each mode contributing 1 R to the specific heat, we have at low T for a diatomic gas cv = 5 R, cp = 7 R, and for a polyatomic gas cv = 3R, cp = 4R. Oscillatory modes obey quantum mechanical laws; they are not excited at low temperatures and contribute in a temperature dependent manner for higher temperatures. Figure 6.18 shows the molar specific heat c¯p = M cp for a variety of ideal gases. Note the temperature independent value for monatomic gases, and the common low temperature value of c¯p = 7 R¯ = 29.1 kJ for diatomic gases.
Air, as a mixture of roughly 78% N2, 21% O2 and 1% Ar, behaves essentially like a diatomic gas, with the low temperature specific heats 2 Rair . As air temperatures rises, so do the specific To simplify computations, one frequently assumes constant specific heats.
To not deviate too much from the actual states, one should use suitable average values cavg , cavg for the temperature interval under consideration, or, alternatively, the values at room temperature. In the latter case one speaks of the cold-gas-approximation, or, for air, cold-air-approximation. Internal energy, enthalpy and entropy are
The cold-gas-approximation, where one uses cavg = cv (T0), works best for relatively low temperatures (e.g., T < 600 K for air), but is highly useful to understand the basic behavior of thermodynamic systems. Constant specific heats allow analytical calculations that give, e.g., explicit expressions for
Fig. 6.18 Molar specific heat at constant pressure c¯p = Mcp for various ideal gases as function of temperature. Note that specific heat of monatomic gases (noble gases) is constant. Based on specific heat data from NIST.
efficiencies that help to further the understanding. Exact engineering calculations must use variable specific heats, of course, and tabulated data must be used, unless the gas is monatomic and the specific heat independent of temperature!