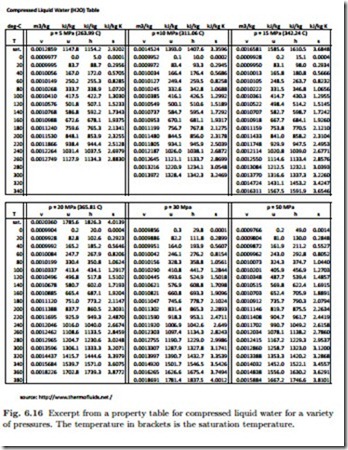
Compressed Liquid
For compressed liquid, i.e., the pure liquid state, only few tables are available, Fig. 6.16 shows a table for compressed liquid water.
Most liquids, including water, are almost incompressible for a wider range of pressures, and this allows us to develop useful approximations that relate compressed liquid properties to those of saturated liquid.
For incompressible fluids a change of pressure does not lead to a change of volume, so that the volume can be approximated by the volume of the saturated liquid,
that is the volume is independent of pressure, but not of temperature. Incompressibility refers to changes at constant temperature, while thermal expansion or contraction are allowed. With this approximation, isothermal lines for the compressed liquid in the p-v-diagram are vertical lines upwards from the saturated liquid line.
Internal energy seen as a function of temperature and volume can then be reduced to its saturated liquid value as well:
For consistency, enthalpy needs to be treated differently. Due to the def- inition h = u + pv, the above approximations give in a first step h (T, p) = uf (T ) + pvf (T ). For the saturated liquid at the same temperature we have hf (T ) = uf (T ) + psat (T ) vf (T ). Combining both by eliminating uf (T ), we find the approximation for the enthalpy of compressed liquid as
For small enough pressures, the correction term for enthalpy can be ignored, so that h (T, p) "’ hf (T ).
Finally, entropy can be treated similar to internal energy,
With this approximation, isobaric lines for the compressed liquid in the T-s- diagram lie on the saturated liquid line.
As an example, we consider compressed liquid water at p = 10 MPa and T = 200 ◦C, for which the table in Fig. 6.16 gives
For this particular example, the approximations yield relative errors below 1%, and even smaller at lower pressures. For higher pressures, however, the relative errors are larger, since compressibility affects all property values, hence these approximations should be used with care. Whenever a full table for compressed liquid states is available, that table should be used. If a table for the liquid states is not available, as is often the case for relatively low pressures, the approximations are quite useful.