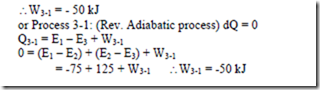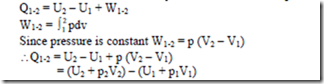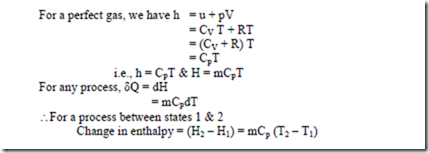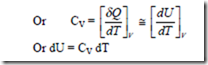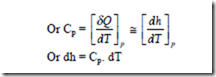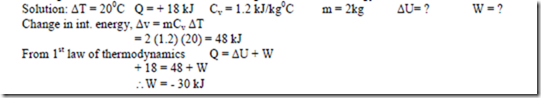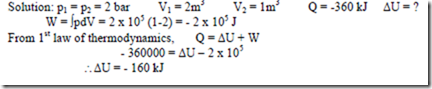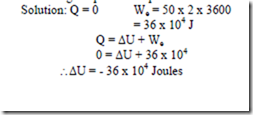Problems on Thermodynamics part1

1. a) An insulated rigid vessel contains some powdered coal and air at a pressure of 10 bar and a temperature of 200 C. The coal is ignited, there results a rise in the pressure and temperature of the contents of the vessel, the final temperature is 5380 C. Taking the vessel and the contents to be the system under consideration evaluate the increase in the energy of the system. b) The insulation is now removed. A heat transfer. of 50 kJ from the system causes the temperature to fall to the initial value, 200 C. Evaluate the increase in the energy of the system during this process. c) Taking the initial energy of the system 32 kJ, write down the energy values after process (a) and after process (b)

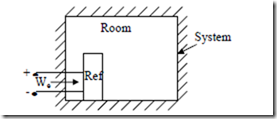
2. On a warm summer day, a housewife decides to beat the heat by closing the windows and doors in the kitchen and opening the refrigerator door. At first she feels cool and refreshed, but after a while the effect begins to wear off. Evaluate the situation as it relates to first law, considering the room including the refrigerator as the system.

Solution:

At first the temperature of air in the room falls since it communicates with the cool refrigerator. This makes the housewife feel cool.

Considering the room and its contents as a system, and assuming walls, windows and doors non- conducting, Q = 0. For the operation of refrigerator, electricity is supplied from outside and hence electrical work We = is done on the system.

From first law of TD Q = ∆E + We

0 = ∆E – We ∆E = We

Positive sign of energy indicates the increase in energy of the system with time. As the energy is increasing, the temperature of air increases and hence effect of coolness gradually begins to wear off.

3. The average heat transfer from a person to the surroundings when he is not actively working is about 950 kJ/hr. suppose that in the auditorium containing 1000 people the ventilation system fails. a) How much does the internal energy of air in the auditorium increase during the first 15 minutes after the ventilation fails? b) Considering the auditorium and all the people as system and assuming no heat transfer. to surroundings, how much does the int. energy of the system change? How do you account for the fact that the temperature of air increases?

Increase in internal energy of the air due to increase in its temperature is compensated by the decrease in internal energy of the people.

4. A household refrigerator is loaded with fresh food and closed. Consider the whole refrigerator and the contents as a system. The machine uses 1 kWhr of electrical energy in cooling the food and the internal energy of the food (system) decreases by 5250 kJ, as the temperature drops. Find the magnitude and direction of heat transfer during the process.

Negative sign indicates heat flows from the refrigerator to the surroundings

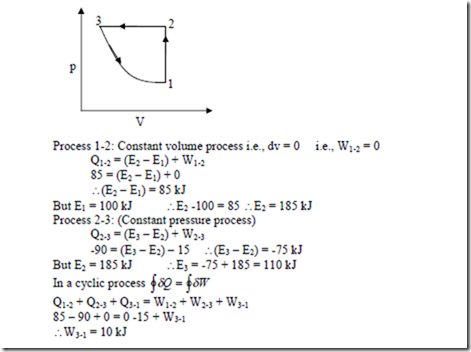
5. A closed system undergoes a constant volume process in which 85 kJ of heat is supplied to it.

The system then undergoes a constant pressure process in which 90 kJ of heat is rejected by the system and 15 kJ of work is done on it. Finally the system is brought back to its original state by a reversible adiabatic process. Determine i) The magnitude and direction of work transfer during the adiabatic process. ii) The energy of the system at all end states if the energy at the initial state is 100 kJ.

Solution:

6. A system undergoes a constant pressure process which is followed by a constant volume process. during the constant pressure process, 125 kJ of heat is transferred to the system and 50 kJ of work is done by the system. during a constant volume process, 125 kJ of heat is rejected from the system. find the work interaction if a rev. adiabatic process restores the system to the initial state.

Solution: Process 1-2: Constant pressure process

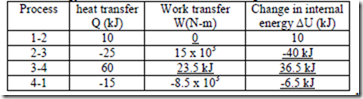
7. A system executes a cyclic process which includes four processes: 1-2, 2-3, 3-4 and 4-1. The magnitudes of the energy transfer are shown in the following table.

Find the magnitude of the unknown quantities in kJ (Hint: For the process 3-4, use ò dU = 0

8. A system composed of a stone having a mass of 10 kg and a bucket containing 100 kg of water are at the same temperature the stone being at a height of 10.2 m above the water level. Stone falls into the water. Determine ∆U, ∆kE, ∆PE, Q and W for the following cases. a) The stone is above to enter the water. b) The stone has just come to rest in the bucket and c) Heat has been transferred to the surroundings in such an amount that the stone and water are at the same temperature they were initially.

Solution: The 1st law of THERMODYNAMICS. is

The Pure Substance

The system encountered in thermodynamics is often quite less complex and consists of fluids that don not change chemically, or exhibit significant electrical, magnetic or capillary effects. These relatively simple systems are given the generic name the Pure Substance.

Definition

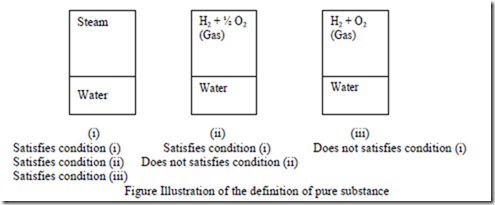
A system is set to be a pure substance if it is (i) homogeneous in chemical composition, (ii) homogeneous in chemical aggregation and (iii) invariable in chemical aggregation.

Homogeneous in chemical composition means that the composition of each part of the system is same as the composition of any other part. Homogeneous in chemical aggregation implies that the chemical elements must be chemically combined in the same way in all parts of the system. Invariable in chemical aggregation means that the chemical aggregation should not vary with respect to time.

In figure three systems are shown. The system (i) shown in the figure is a mixture of steam and water. It is homogeneous in chemical composition because in every part of the system we have, for every atom of oxygen we have two atoms of hydrogen, whether the sample is taken from steam or water. The same is through for system (ii) consisting of water and uncombined mixture of hydrogen and oxygen. System (iii) however is not homogeneous in chemical composition because in the upper part of the system hydrogen and oxygen are present in the ratio 1:1 where as in the bottom portion they are present in the ratio 2:1.

System (i) also satisfies condition (ii), because both hydrogen and oxygen have combined chemically in every part of the system. System (ii) on the other hand does not satisfies condition (ii) because the bottom part of the system has two elements namely hydrogen and oxygen have chemically combined where as in the upper part of the system the (ii) elements appear as a mixture of two individual gases.

Invariable in chemical aggregation means that the state of chemical combination of the system should not change with time. Thus the mixture of hydrogen and oxygen, if it is changing into steam during the time the system was under consideration, then the systems chemical aggregation is varying with time and hence this system is not a pure substance. Thus the system (i) is a pure substance where as the systems (ii) and (iii) are not pure substances. The Two Property Rule for a Pure Substance

The thermodynamics state of a pure substance of a given mass can be fixed by specifying two independent properties provided (i) the substance is in equilibrium and (ii) the effects of gravity, motion, capillarity, electricity and magnetism are negligible.

The above rule indicates that if the values of two properties of a pure substance are fixed then the values for all other properties are fixed. This means that there is a definite relation between the two independent properties and each of the other properties. Each of these relations is called “Equation of state” for a pure substance. The equation of state for a pure substance can be in any one of the following forms: (i) Algebraic equation (example: perfect gas equation), (ii) Tables (example: steam tables) and (iii) Charts (example: Mollier chart for steam).

Specific heat, C

When interaction of heat takes place between a closed system and its surroundings, the internal energy of the system changes. If δQ is the amount of heat transferred to raise the temperature of 1 kg of substance by dT, then, specific heat C = δQ/dT

As we know, the specific heat of gas depends not only on the temperature but also upon the type of the heating process. i.e., specific heat of a gas depends on whether the gas is heated under constant volume or under constant pressure process.

We have dQ = m CV. dT for a rev. non-flow process at constant volume and dQ = m Cp. dT for a rev. non-flow process at constant pressure For a perfect gas, Cp & CV are constant for any one gas at all pressure and temperatures. Hence, integrating above equations.

Flow of heat in a rev. constant pressure process = m Cp (T2 – T1)

Flow of heat in a rev. constant volume process = m CV (T2 – T1)

The internal energy of a perfect gas is a function of temperature only. i.e, u = f (T), to evaluate this function, let 1 kg of gas be heated at constant volume

From non-flow energy equation, δQ = dU + δW

Enthalpy: Consider a system undergoing a quasi equilibrium constant pressure process. We have from 1st law of thermodynamics for a non-flow process,

i.e ., heat transfer during the process is given in terms of the change in the quantity (U + pV) between initial and final states. Therefore, it find more convenient in thermodynamics to define this sum as a property called Enthalpy (H)

i.e., H = U + pV

In a constant pressure quasi equilibrium process, the heat transfer is equal to the change in enthalpy which includes both the change in internal energy and the work for this particular process.

The enthalpy of a fluid is the property of the fluid, since it consists of the sum of a property and the product of the two properties. Since enthalpy is a property, like internal energy, pressure, specific volume and temperature, it can be introduced into any problem whether the process is a flow or a non-flow process.

Specific heat at Constant Volume:

When heat interaction takes place at constant volume, δW = 0 and from 1st law of thermodynamics, for unit mass, (δq)V = dU

The amount of heat supplied or removed per degree change in temperature, when the system is kept under constant volume, is called as the specific heat at constant volume,

Specific heat at Constant pressure

When heat interaction is at constant pressure, (δq)p = dh

The amount of heat added or removed per degree change in temperature, when the system is kept under constant pressure, is called as the specific heat at constant pressure.

Application of 1st law of thermodynamics to non-flow or closed system:

a) Constant volume process (V = constant)

Applying 1st law of thermodynamics to the process,

The above equation is true for an adiabatic process whether the process is reversible or not. In an adiabatic experiment, the work done W1-2 by the fluid is at the expense of a reduction in the internal energy of the fluid. Similarly in an adiabatic composition process, all the work done on the fluid goes to increase the internal energy of the fluid.

To derive pVg = C: For a reversible adiabatic process

In a poly tropic process, the index n depends on the heat and work quantities during the process.

9. A cylinder contains 0.45 m3 of a gas at 1 bar & 800C. The gas is compressed to a volume of 0.13 m3, the final pressure being 5 bar. Determine i) the mass of the gas, ii) the value of index ‘n’ for composition, iii) the increase in internal energy of the gas and iv) the heat received or rejected by the gas during compression. (Take g = 1.4, R = 294.2 J/kg-K).

11. A fluid system consisting of 4.17 kg of a pure substance has an energy E of 85 kJ. The kinetic energy of the system is 17 kJ and its gravitational potential energy is 5 kJ. The system undergoes an adiabatic process in which the final sp. i.e., is 150 kJ/kg, the final kinetic energy is 1.9 kJ and the final gravitational potential energy is 1.1 kJ. The effects due to electricity, capillary and magnetism are assumed to be absent. a) Evaluate the initial value of the sp. i.e., of the fluid. b) Determine the magnitude and sign of the work done during the process.

14. A closed system of constant volume experiences a temperature rise of 200C when a certain process occurs. The heat transferred in the process is 18 kJ. The specific heat at constant volume for the pure substance comprising the system is 1.2 kJ/kg0C, and the system contains 2 kg of this substance. Determine the change in the internal energy and the work done.

15. The stationary mass of gas is compressed without friction from an initial state of 2 m3 and 2 x 105 N/m2 to a final state of 1 m3 and 2 x 105 N/m2, the pressure remaining the same. There is a transfer of 360 kJ, of heat from the gas during the process. How much does the internal energy of the gas change?

16. The internal energy of a certain substance is given by the following equation u = 3.56 pv + 84 where u is given in kJ/kg, p is in KPa and v in m3/kg. A system composed of 3 kg of this substance expands from an initial pressure of 500 KPa and a volume of 0.22 m3 to a final pressure of 100 KPa in a process pv1.2 = constant. i) If the expansion is quasi- static, find Q, DU, and W for the process. ii) In another process the same system expands according to the same pressure volume relationship as in part (i) and from the same initial state to the same final state as in part (i) but the heat transfer in this case is 30 kJ. Find the work transfer for this process. iii) Explain the difference in work transfer in parts (i) and (ii).

17. A fluid is contained in a cylinder by a spring-loaded, frictionless piston so that the pressure in the fluid is a linear friction of the volume (p = a + bv). The internal energy of the fluid is given by the following equation, U = 34 + 3.15 pV where U is in kJ, p is in kPa and V in m3. If the fluid changes from an initial state of 170 kPa, 0.03 m3 to a final state of 400 kPa, 0.06 m3, with no work other than that on the piston, find the direction and magnitude of the work and heat transfer.

18. A piston cylinder arrangement has a gas in the cylinder space. During a constant pressure expansion to a larger volume the work effect for the gas are 1.6 kJ, the heat added to the gas and cylinder arrangement is 3.2 kJ and the friction between the piston and cylinder wall amounts to 0.24 kJ. Determine the change in internal energy of the entire apparatus. (Gas, cylinder, piston).

19. A system receives 42 kJ of heat white expanding with volume change of 0.123 m3 against an atmosphere of 12 N/m2. A mass of 80 kg in the surroundings is also lifted a distance of 6 mts.

i) Find the change in energy of the system. ii) The system is returned to its initial volume by an adiabatic process which require 100 kJ of work. Find the change in energy of the system.

iii) Determine the total change in energy of the system.

20. A thermally insulated battery is being discharges at atmosphere pressure and constant volume. During a 1 hr test it is found that a current of 50A and 2v flows while the temperature increases from 200C to 32.50C. Find the change in internal energy of the cell during the period of operation.