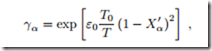Problems
Ammonia and Water
Absorption refrigeration systems often employ two phase equilibrium mixtures of ammonia (NH3) and water (H2O). For the following problems, assume an ideal mixture:
1. A liquid-vapor mixture of ammonia and water at 30 ◦C has a mole fraction of ammonia in the liquid of 60%. Determine the mole fractions of water and ammonia in the vapor phase, and the total pressure of the mixture. Saturation pressure of NH3 at psat(30 ◦C) = 1116.5 kPa.
2. A two-phase mixture of ammonia and water is in equilibrium at 50 ◦C. The composition of the vapor phase is 99 percent NH3 and 1 percent H2O by mole numbers. Determine the composition of the liquid phase and the total pressure. Saturation pressure of NH3 at 50 ◦C is 2033.5 kPa.
3. A liquid-vapor mixture of ammonia and water is at 40 ◦C and 1000 kPa.
Determine the mole fractions of water and ammonia in the vapor and liquid phase. Saturation pressure of NH3 at psat(40 ◦C) = 1554.33 kPa.
4. A liquid-vapor mixture of ammonia and water is in equilibrium at 10 ◦C and 500 kPa. Determine the mole fractions of water and ammonia in the vapor and liquid phase. Saturation pressure of NH3: psat (10 ◦C) = 615.29 kPa.
Binary Mixture of Propane and 1-Butane I
1. Use the idealized Raoult law to find the mole fractions
2. Determine the mole numbers
Binary Mixture of Propane and 1-Butane II
Consider a mixture of n1 = 25 kmol propane (C3H8) and n2 = 100 kmol 1- butane (C4H10), at T = 350 K and p = 12 bar. The saturation pressures of the pure substances can be found from the Antoine equation ln psat , where the pressure is measured in bars, the temperature in K, and the constants have the values
Binary Mixture of Propane and 1-Butane III
Binary Mixture of Propane and 1-Butane IV
Consider an ideal two phase mixture of propane (C3H8) and butane (C4H10), at temperature of 330 K. At this temperature, the saturation pressures of propane and butane are 19.4 bar and 5.86 bar, respectively. The mixture is equimolar, with 220 kmol of each component present, and the mole fraction of butane in the vapor phase is 30%.
1. Determine the mole fractions of butane and propane in both phases.
2. Determine the pressure of the mixture, p .
3. Determine the total mole number in the liquid.
Phase Diagrams for Propane and 1-Butane
Construct phase diagrams for a mixture of propane and 1-butane (ideal mixture). Use a computer with suitable software for plotting and evaluating of equations.
The saturation pressures of the pure substances can be found from the
where the pressure is measured in bar, and the temperature in K.
1. Construct and plot the p-X phase diagram for a variety of temperatures (stay in between critical and triple points!).
2. Construct and plot the T-X diagram for a variety of pressures.
Water and R134a
Mixtures of water and refrigerant are used in self-foaming products. Consider a mixture of 120 g R134a (molar mass 102 g ) and 50 g water, initially at 20 ◦C and 2 bar, later at 20 ◦C and 1 bar.
1. Find the overal mole fraction of R134a in the mixture.
2. Find the mole fractions for both pressures. Use the idealized Raoult law.
3. Draw a p-X-diagram for the mixture, and indicate the two states and the overall mole fraction in the diagram. Carefully consider whehter the mixture is all liquid, liquid-vapor mix, or all vapor.
4. Determine the mole numbers for both states.
5. Assuming ideal mixtures for both phases, determine the volume change of the system.
Saturation Temperature and Pressure
1. Pure water at p = 1 bar boils at a temperature of 99.63 ◦C. How much salt must be added per kg of water to lower the saturation pressure for the same temperature by 1%?
2. For the same solution, find the boiling temperature for a pressure of 1.5 bar.
Note: NaCl dissociates in solution.
Water and Salt
A solution of salt (NaCl, MNaCl = 58.5 kg) in water at 1.5 bar has a boiling temperature of 112 ◦C. How many grams of salt are dissolved in one litre of water?
Note: NaCl dissociates in solution.
Increase of Boiling Temperature
50 g sodium chloride are dissolved in 1 litre of water. Compute the boiling temperature at 1 bar.
Melting
In winter, after ice rain, a street is covered with a 1 cm thick layer of ice. What is the minimum mass of salt (NaCl) required per square meter to melt the ice when the temperature is −10 ◦C?
Cooling Liquid for a Car
The coolant of a car is required to freeze only below −20 ◦C. How many moles of ethylene glycol (C2H6O2) or NaCl must be mixed to water, in order to lower the temperature of freezing to the required value? Why is glycol preferable above NaCl?
Cooking Pasta in the Mountains
A cylindrical pot (base area 250 cm2, height 25 cm) contains 4 kg of pure water and 2 mol of NaCl. A lid which has a mass of 500 g rests freely on the top of the pot. The outside pressure is 0.8175 atm. At what temperature will the saltwater in the pot start to boil?
Boiling Point
100 g of glucose (C6H12O6) and 20 g NaCl are dissolved in one litre of water, the mixture can be described as ideal mixture.
1. Find the boiling temperature of this mixture on a mountain, where the local pressure is 0.75 bar.
2. Determine the minimum work to remove only the salt, when the temperature is 23 ◦C.
A Lake
A lake in the mountains has a surface area of 1.2 km2, its average depth is 24 m, and the water temperature is 17 ◦C. Air (XN2 = 0.79, XCO2 = 0.0004) at 0.8 bar stands over the water. Compute the masses of dissolved nitrogen and carbon dioxide.
Gas Mixture
Water is in contact with a gaseous mixture of nitrogen and carbon dioxide. The mole fractions of the gases in the liquid phase are measured as 1.1 × 10−4 for nitrogen and 0.006 for carbon dioxide. For a temperature of 25 ◦C, determine the mole fraction in the gas mixture, and the overall gas pressure.
Carbon Dioxide in Water
A piston cylinder system, which is maintained at a temperature of 298 K, contains 1 litre of liquid water, water vapor, and 5 g of carbon dioxide. The gas phase fills a volume of 1/10 litre.
1. Determine the pressure in the system.
2. Determine the percentage of CO2 that is dissolved.
Hint: The solution becomes much easier with the assumption that in the liquid the mole amount of CO2 is much smaller than the mole amount of water. If you use the assumption, verify it.
Henry’s Law: Sparkling Water
A bottle of volume V = 1.05 litre contains 1 litre of liquid water, water vapor, and carbon dioxide. The pressure in the bottle is 2 bar at a temperature of 55 ◦C. Compute the masses of water and CO2 in the bottle. Consider vapor and gaseous CO2 as ideal gases. Ignore the volume (but not the amount) of dissolved CO2 . Henry’s law constant for CO2: HCO2 (55 ◦C) = 3200 bar.
Henry’s Law: Nitrogen in Water I
A bottle of volume V = 0.55 litre contains 0.5 litre of liquid water, water vapor, and nitrogen. The pressure in the bottle is 1.5 bar at a temperature of 35 ◦C. Compute the masses of water and N2 in the bottle. Consider vapor and gaseous N2 as ideal gases. Ignore the volume of dissolved N2. Henry’s law constant for N2: HN2 (35 ◦C) = 98600 bar.
Remark: Guinness beer is nitrogenated with a special tab. This problem shows, why bottling it might give a very flat beer, unless a “widget” is used.
Henry’s Law: Nitrogen in Water II
A bottle of total volume V = 0.55 litre contains 0.5 litre of liquid water, some water vapor, and a total of 0.006 mol of nitrogen. The temperature of the bottle and its contents is 35 ◦C.
1. Compute the total mass of water in the bottle (use tables).
2. Determine the amounts of nitrogen (in moles) dissolved in the liquid, and in the gas phase.
3. Determine the pressure in the bottle.
For the solution, ignore the volume (but not the amount) of dissolved N2. Henry’s law constant for N2: HN2 (35 ◦C) = 98600 bar.
A Diver
A deep sea diver breathes a mixture of 21% O2 and 79% He, which is at the local water pressure. The divers body contains 5 litre of blood; for simplicity, assume that blood behaves like water.
1. Assume the blood (i.e., water at 36oC) saturates with helium, and deter- mine the amount (in moles) of helium dissolved in the blood at sea level and at a depth of 200 m.
2. For both cases determine also the volume (in litre) that the helium assumes at standard conditions.
3. Explain in thermodynamic terms why the driver needs to decompress slowly.
Henry’s Law: Measurement of Oxygen Content of Lake Water In order to retrieve water from deeper layers of a lake, the following simple device is suggested: A cylinder of volume V = 0.11 litre is filled with helium at 2 bar. The device is brought to the desired depth, and a valve is opened which allows water to enter the system, while the helium remains inside. Then the system is brought to the surface, and a sample of the water is taken to analyze the oxygen content.
The temperatures of all gases and liquids are assumed to be 9 ◦C, and the pressure on top of the lake is 0.9 bar. Density of water is 1 kg/litre. Henry’s constant for O2 in water at 9 ◦C is HO2 (T ) = 31200 bar.
1. 100 ml of water enter the system—estimate the depth at which the valve was opened.
2. It is measured that the mole fraction of oxygen in the water sample is 1.1 × 10−6. Use this information to compute the mole fraction of oxygen in the water where the sample was taken.
Hint: Obviously, some of the oxygen will gas out and enter the gas volume spanned by the helium, and this leads to a lower gas content in the liquid.
Measurement of Henry’s Constant
To measure Henry’s constant for oxygen in water, the following device is suggested. A container is divided into two equal parts, one part is filled with highly purified water, the other part is filled with oxygen at 10 bar. Then, the division is removed, and oxygen and water assume an equilibrium state.
The gas pressure is measured as 9.66 bar, and throughout the measurement the temperature is kept at 20 ◦C. Determine Henry’s constant HO2 (T ), and the relative amount of oxygen that enters the liquid.
Hint: Ignore the change in volume due to oxygen entering the liquid.
Henry’s Law: Mass of CO2 In Air and Oceans
1. On earth, the pressure at ground level is 1 atm = 1.01325 bar, the gravitational acceleration is 9.81 m , and the earth radius is 6300 km. Use this data to compute the mass of the atmosphere.
2. 0.04 mole% of the air is carbon dioxide (CO2) and 20.95 mole% is oxygen (O2). Compute the masses of CO2 and O2 in the atmosphere.
3. 70% of the earth is covered by oceans and the average depth of the oceans is 4000 m. Assuming the mass density of the oceans is 1000 kg , compute the mass of water in the oceans.
4. For an average water temperature of 4 ◦C, compute the masses of CO2 and O2 dissolved in the worlds oceans. Use Henry’s law in the form where Hα (T ) is Henry’s law constant.
Comment: This problem assumes equilibrium conditions and ignores chemical effects. The actual amount of CO2 dissolved differs from the value obtained here, due to formation of carbonic acid and carbonates, as well as non-equilibrium conditions.
Azeotropic Curves
Consider a binary mixture in liquid-vapour equilibrium, for two substances whose vapor pressures follow the Antoine law ln p = A − B , where p is pressure in bar, and T is the temperature in Kelvin, with
Assume that the vapor can be described as an ideal gas, while the activity coefficients in the liquid phase are given as
where ε0 is a measure for the energy of interaction between particles of different type and T0 = 300 K.