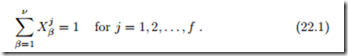Phase Equilibrium in Mixtures:Phase Mixtures and Gibbs’ Phase Rule.

Phase Mixtures

In this chapter we discuss equilibria between mixtures in diﬀerent phases, e.g. liquid-vapor equilibria, or liquid-solid equilibria. Phase mixtures normally are characterized by diﬀerent mole fractions (or concentrations) in the diﬀerent phases. We shall discuss phase diagrams, changes of melting and evaporation temperatures in solutions, distillation processes, and gas solubility.

Gibbs’ Phase Rule

In extension to our previous notation we introduce Latin superscripts to de- note the phases, and we assume that we have f diﬀerent phases. For instance α (α = 1,... , ν, j = 1,,... ,f ) denotes the mole fraction of component α in phase j. Also, μj (T, p, Xj is the chemical potential of component α in phase j; note that the chemical potential depends only on the mole fractions of the same phase.

For each phase, the mole fractions sum to unity, that is

It follows that a mixture with ν components in f phases is characterized by (ν − 1) f independent mole fractions. In addition, pressure p and temperature T are variables, so that the mixture is characterized by (ν − 1) f + 2 intensive variables, {p, T , X j .

Phase boundaries are permeable interfaces between phases that allow all components to pass, and thus in equilibrium the chemical potentials of all components must be continuous between any two phases,

These equations are known as Gibbs’ phase rule, and they give (f − 1) ν conditions1 that restrict the (ν − 1) f + 2 variables. The diﬀerence between these numbers gives the number of degrees of freedom for the system,

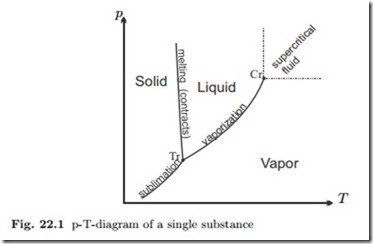
Figure 22.1 shows again a sketch of the p-T-diagram of a single substance (for water, actually) with the saturation curves and the triple point.

Liquid-Vapor-Mixtures: Idealized Raoult’s Law

We study vapor-liquid equilibrium in mixtures where we denote the liquid phase by / and the vapor phase by //. The Gibbs phase rule for this case reads

Our goal is to simplify the phase rule by using constitutive equations for incompressible liquids and ideal gases, respectively. Deviations from this idealized behavior will be studied later. In particular, we make the following assumptions:

1. The liquids are ideal mixtures, so that

When we use the four assumptions in (22.4) together with the deﬁni- tion of the saturation pressure of the single components, g¯/ (T, psat (T )) = α (T, pα (T )), we ﬁnd Raoult’s law for ideal mixtures (Franc¸ois-Marie Raoult, 1830-1901)

The partial pressure of α in the vapor is given by pα = X //p. Raoult’s law states that the amount of component α in the liquid is proportional to its partial pressure in the vapor.