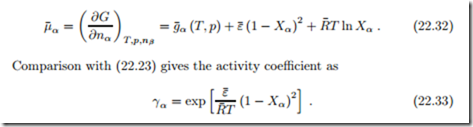A Simple Model for Heat of Mixing and Activity
Ideal mixtures have zero enthalpy of mixing Hmix, and their activity coefficients are unity. We shall now develop a simple model for Hmix to describe non-ideal behavior. We consider binary mixtures only.
Part of the internal energy of a substance comes from the interaction potential between neighboring molecules. For a component alone, this contribution to energy is included in enthalpy h¯α (T, p) or free energy g¯α (T, p), and we can consider identical neighboring particles as energetically neutral.
In a mixture between components 1 and 2, there will be neighboring pairs of the same type (1-1, 2-2) and pairs of different type (1-2). While the former are energetically neutral, the formation of the latter can either release or require energy. When the attractive force between different particles (1-2) is stronger than that between equal particles (1-1, 2-2), 1-2 pairs are energet ically preferred over neutral pairs, due to negative interaction energy; then energy is released when a mixed pair (1-2) is formed. When the attractive force between different particles (1-2) is weaker than between equal particles (1-1, 2-2), neutral pairs are energetically preferred over (1-2) pairs, due to positive interaction potential; then energy is required to form a pair.
We consider a mixture of N = N1 + N2 particles of types 1, 2. The probability to find a particle of type α is Nα and thus the probability to find a pair (1-2) is proportional to N1 N2 . The total number of pairs is of the order of the total number of particles N , and thus the number of (1-2) pairs is proportional to N N1 N2 = N1 N2 . When we introduce mole numbers, the enthalpy of mixing is
The chemical potential is the derivative of the total Gibbs free energy (20.2),