Placement Based Representations
The placement-based representations include sequence pair, bounded-sliceline grid, corner block list and slicing tree. With the dimensions of all the blocks known, the sequence pair and bounded-sliceline grid can be applied to general floorplans. The corner block list records the relative position of adjacent blocks, and is applicable to mosaic floorplan only. The slicing tree is for slicing floorplan, which is a special case of mosaic floorplan.
Sequence-Pair
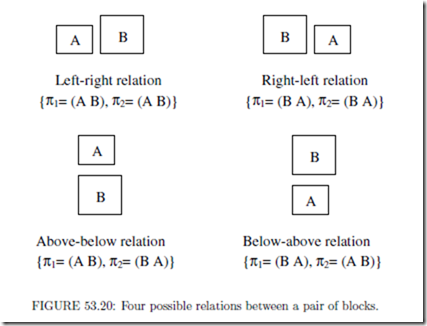
Sequence-pair expresses the topological positions of blocks with a pair of block lists [5][18]. For each pair of blocks, there are four possible relations, left-right, right-left, above-below, and below-above. We use a pair of sequences {π1, π2} to record the order of the two blocks. We can record two blocks A, B in four different orders: (AB, AB), (AB, BA), (BA, AB), (BA, BA). Hence, we use the four orders to represent the four placement relations.
Fig. 53.20 shows the four possible relations between a pair of blocks A and B and the corresponding sequence pair for each relation.
The two sequences can be viewed as two coordinate systems that define a grid placement
of the blocks. To see it more clearly, we construct a grid system illustrated in Fig. 53.21. The slopes are denoted with the labels of blocks according to their orders in the two sequences. The intersections of two perpendicular lines that have the same label indicate the topological positions of the blocks.
The grid placement defines the floorplan relation between blocks. For each node in the grid placement, we divide the whole space into four quadrants, quadrant I: –45 to 45 degrees, quadrant II: 45 to 135, quadrant III: 135 to 225, quadrant IV: 225 to 315. Block B’s floorplan relation with block A can be derived from block B’s location in block A’s quadrants.
1. Quadrant I: block B is on the right of block A
2. Quadrant II: block B is above block A
3. Quadrant III: block B is on the left of block A
4. Quadrant IV: block B is below block A
For example, from the grid placement in Fig. 53.22, using node d as a reference, blocks e and f are on the right of block d; blocks g and h are above; blocks c is on the left; and blocks a and b are below.
We can derive the sequence-pair from a floorplan by tracing the blocks through two directions. We first extend the boundary of each block by drawing lines from its four corners (Fig. 53.22). In Fig. 53.22(a), we draw a line from the upper-right corner of each block that goes either rightward or upward. When the line is obstructed with a block or an already existing line, it changes its direction. The extension of the line ends when it reaches the boundary of the chip. We also draw a line from the lower-left corner of each block that goes either downwards or leftwards. The extended lines partition the chip into zones. Following the order of the zones, we get a label sequence. For instance, we have π1 =! ecaf dg! for Fig. 53.22(a). With similar operations, the second sequence is derived in the orthogonal direction (π2 =! f cegad! in Fig. 53.22(b)). π1 and π2 consist of a sequence-pair, which involves all the information of the topological positions of blocks.
For translating a sequence-pair into a topological floorplan with n blocks, a brute force implementation requires time complexity O(n2), since there are O(n2) pairs of blocks and we need to scan all the pairs to get the constraint graph and then derive the floorplan by performing a longest path computation. In [8], a fast algorithm with O(nloglogn) time complexity is proposed to complete the transformation of a sequence pair to the floorplan. The fast algorithm takes advantage of the longest common sequence of the two sequences in a sequence-pair. They show that the longest common sequence calculation is equivalent to the longest path computation in the constraint graph for a sequence-pair. The authors use a priority queue data structure to record the longest common sequence, thus reduce the time for calculating the position of a single block to O(loglogn) by amortizing. The representation of a sequence-pair has the following properties:
1. The number of bits for storing a sequence-pair is 2n log2 n, where n is the number of blocks in the placement.
2. The time complexity of translating a sequence-pair into a topological floorplan is n log2 log2 n by the newest report.
3. There are totally (n!)2 possible sequence-pairs for n blocks. However, there exists
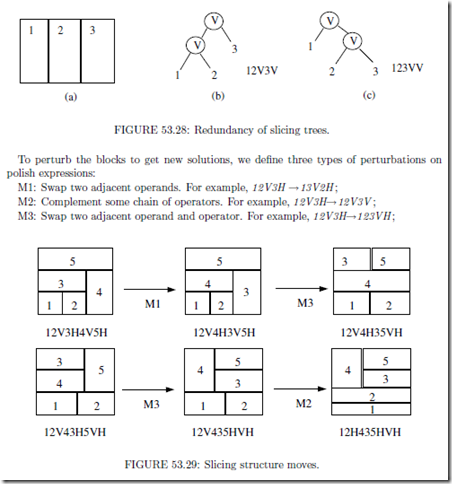
the redundancy. For example, the sequence-pairs in Fig. 53.21(a) and (c) actually correspond to the same placement (Fig. 53.21(b)).
Bounded-Sliceline Grid
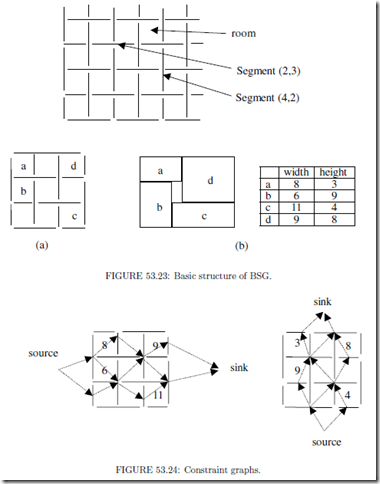
Another method rising from the same idea as sequence-pair is BSG [6], where, instead of the intersections of grid lines, the squares surrounded by the grid lines, called rooms, are used to assign the blocks (Fig. 53.23).
Although put forward aiming at the packing problem, BSG can also act as a compacting algorithm to determine the accurate positions of blocks. In BSG, grid lines are separated into vertical and horizontal segments (Fig. 53.23). Two constraint graphs are set up with their vertexes corresponding to the grid segments and their directed edges corresponding to the relative positions of the grid segments (Fig. 53.24). The vertexes ‘source’ and ‘sink’ are added to make the operation on the graph easy. Every room is crossed by one edge of the constraint graph (respectively in the vertical and horizontal constraint graphs). If the room is not empty, or there is a block assigned into the room, the crossing edge has a weight equal to the width (in the horizontal graph) or the height (in the vertical graph) of the assigned block, otherwise the crossing edge has a weight of zero. Fig. 53.24 shows the weights derived from the example in Fig. 53.23. By calculating the longest path lengths between the source and the other vertexes in the constraint graphs the real coordinates of the grid segments can be determined and in fact the translation to the placement is implemented.
Table 53.4 gives the final results of the example in Fig. 53.23
and Fig. 53.24. Notice that segment (1, 3) and (2, 2) have the same position, for the edge between the two vertexes in the horizontal constraint graph has the weight of zero.
Due to the homology, BSG has the similar performance as sequence-pair, except that the complexity of the translation into placement, or finding the longest path lengths for all the vertexes in the constraint graphs, is O(pq), provided that the grid array has p columns and q rows.
Corner Block List
Corner block list is a third method of representing non-slicing structures [4][19][20]. Refer to Fig. 53.25. The floorplan is required to be mosaic and without degeneration.
For every block, the T-junction at the bottom-left corner can be in either of the two directions. Accordingly we say the orientation of the block is 1 or 0 respectively. Now
let’s observe the most upper-right blocks in Fig. 53.25(a) and (b), both denoted with ‘d’. If we push the bottom boundary of block ‘d’ in (a) upwards, or the left boundary in (b) rightwards, then block ‘d’ is squeezed and finally deleted (Fig. 53.25(c) and (d)), and thereafter block ‘a’ becomes the most upper-right block. The operation of squeezing and deleting can be repeatedly performed until there is only one block left in the placement.
According to the order in which the blocks are squeezed out, we get two lists. The labels of blocks are stored in list ‘S’ while the orientations of the blocks in list ‘L’. For example,
for Fig. 53.25(a), S= ‘fcegbad’ and L= ‘001100’. S and L are not sufficient to recover the placement, so we need the third list, T . Each time we squeeze a block, we record the number of T-junctions on the moving boundary, excluding the two at its ends, then add the same number of ‘1’s and one ‘0’ into T . For example, in Fig. 53.25(a), when squeezing block d, we have T = ‘01’, for there is only one T-junction on the bottom boundary, which separates the blocks a, d and g. Next, while squeezing block a, only a ‘0’ is added to T , for there is no T-junction on the bottom boundary of block a. Consequently, we have T = ‘001’ after the deletion of block a, and T=‘00101001’ after the deletion of block c. With an inverse process, the placement can be recovered from S, L and T .
The performance of corner block list is:
1. The storage of the 3 lists needs at most n(3 + logn) bits.
2. The number of combinations is T RIALREST RICTION , which is the same as that of a slicing tree. However, slicing structure only covers part of all possible combinations, therefore has larger redundancy than corner block list.
3. The complexity of the translation between placement and lists is T RIALREST RICTION .
Slicing Tree
A floorplan is call a slicing structure [7][29] if it can be iteratively partitioned into two parts with vertical or horizontal cut lines throughout the separated parts of the area, until the individual blocks.
Fig. 53.26(a) gives an example. Line 1 splits the whole layout into two parts. The left half involves only one block but the right half can been further split by line
2. Then follows line 3, line 4, and so on. On the contrary, Fig. 53.26(b) is a non-slicing structure. We can’t find a cut line throughout the floorplan to split it into two parts.
Now that a slicing floorplan can been iteratively split into two parts with vertical or horizontal cut lines, a binary tree can be structured according to the splitting process.[13] Fig. 53.27 gives an example of a slicing floorplan and its binary tree. The inter nodes on the tree denoted with “H” or “V” indicate the direction of the line splitting the areas, while the leaf nodes correspond to the blocks. We call the binary tree a slicing tree.
Just as in twin binary tree, we hope to find a simple data structure to express the slicing tree. Polish Expression is a good solution. It is the result of a post-order traversal on the slicing tree. As an example, the Polish Expression of Fig. 53.27 is: 123V56V8H47HVHV. We regard “H” and “V” as operators and the blocks operands.
Formally, we have the following definition for a Polish expression:
![]() A sequence b1b2…b2n 1of elements from {1, 2, …, n, V,H} is a Polish expression of
A sequence b1b2…b2n 1of elements from {1, 2, …, n, V,H} is a Polish expression of
1. Every subscript i appears exactly once in the sequence, 1≤i≤ 2n-1.
2. The number of operators is less than the number of the components for any prefix sub-string.
So needless to re-construct the slicing tree, we are able to judge a legal Polish Expression. For example, 21H57V43H6VHV and 215H7V43H6VHV are legal Polish Expressions while 215HVHV7436HV and 2H15437VVVHH are not. An illegal Polish Expression can’t be converted to a binary tree.
It is obvious that for a given slicing tree, we have a unique Polish Expression. Inversely, we can easily conduct the slicing tree according to its Polish Expression. So we conclude that there is a one-to-one correspondence between the slicing tree and Polish Expression. However, there may be more than one slicing tree corresponding to one floorplan, as shown in Fig. 53.28. Thus there exists redundancy. To compact the solution space, we define the skewed slicing tree to be a slicing tree without a node that has the same operator as its right son. Correspondingly, a normalized Polish expression is defined:
A Polish expression b1b2…b2n−1 is called to be normalized iff there is no consecutive “V” or “H” in the sequence.
In Fig. 53.28, (b) is a normalized Polish expression while (c) is not. There is a one-to- one correspondence between the set of normalized Polish expressions and the set of slicing structures.
The operation of M3 may result in a non-normalized Polish Expression. So a check is necessary after an operation of M3 to guarantee that a normalized expression is generated. Fig. 53.29 illustrates two sequences of polish expression transformations as well as their corresponding floorplans. We can see that a slight modification on the Polish Expression can result in a completely different floorplan topology. This is just what we want.
Finally, we analyze the performance of slicing tree.
1. Given a floorplan of n blocks, the slicing tree contains n leaves and n − 1 internal nodes.
2. The number of possible configurations for the tree is O(n!·2 3n−3·n1.5).
3. The storage of a Polish Expression needs a 3n-bit stream plus a permutation of n blocks.
4. It will take linear time to transform a floorplan into a slicing tree, and vice versa.