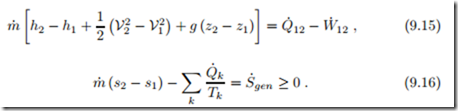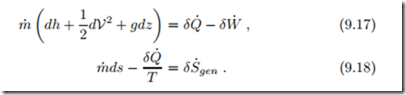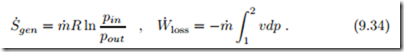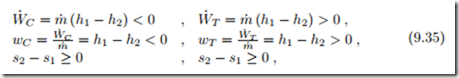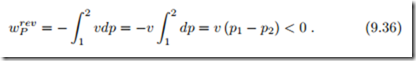One Inlet, One Exit Systems
A case of particular importance are systems with only one inlet and one exit, as sketched in Fig. 9.4, for which the mass balance reduces to
There is just one constant mass flow m˙ the system. flowing through each cross section of The corresponding forms for energy and entropy balance are
It is instructive to study the equations for an infinitesimal step within the system, i.e., for infinitesimal system length dx, where the differences reduce to differentials,
Heat and power exchanged, and entropy generated, in an infinitesimal step along the system are process dependent, and as always we write (δQ˙ , δW˙ , δS˙ )
to indicate that these quantities are not exact differentials. Use of the Gibbs equation in the form T ds = dh − vdp allows to eliminate dh and δQ˙ between the two equations to give an expression for power,
The above equation has several implications: First, since T δS˙gen ≥ 0, we see—again—that irreversibilities reduce the power output of a power pro- ducing device (where W˙ 12 > 0), and increase the power demand of a power consuming device (where W˙ 12 < 0). Efficient energy conversion requires to reduce irreversibilities as much as possible.
When we consider (9.19) for a flow without work, we find Bernoulli’s equation (Daniel Bernoulli, 1700-1782) for pipe flows as
For flows at relatively low velocities and without significant change of level the above relation can be simplified to
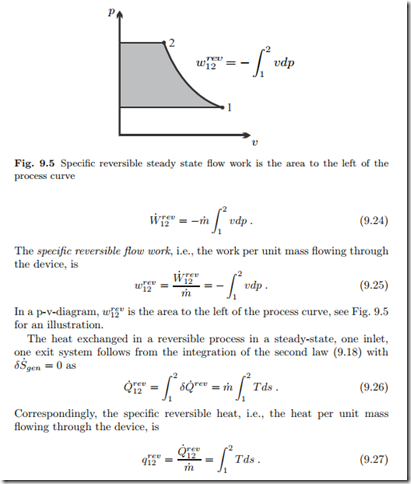
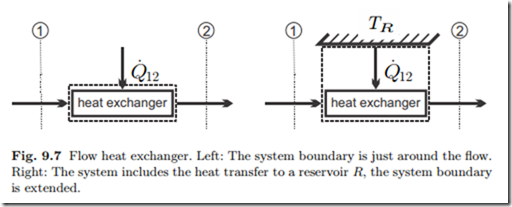
In a T-s-diagram, qrev is the area below the process curve, just as in a closed system.
Entropy Generation in Mass Transfer
Friction in flows leads to loss of pressure and corresponding entropy generation. When we consider a simple flow with no work added or withdrawn, Eq. (9.21) gives the entropy generated in dx as
We interpret the entropy generation rate as the product of a flux, the mass flow m˙ , and a thermodynamic force, namely the integral over − v dp. Since specific volume v and thermodynamic temperature T are strictly positive, the force r out v dp is proportional to the pressure difference, − r out v dp ∝ (pin − pout). In order to obtain a positive entropy generation rate, the mass flow must be proportional to the force, which is the case for
Here, A is the mass transfer area and β > 0 is a positive transport coefficient that must be measured.
One particular example for this law is the Hagen-Poiseuille relation (Gotthilf Hagen, 1797-1884; Jean Poiseuille, 1797-1869) of fluid dynamics which gives the volume flow V˙= m˙ /ρ of a fluid with shear viscosity η through a pipe of radius R and length L as
Another example for (9.30) is Darcy’s law (Henry Darcy, 1803-1858) that describes flow through porous media. Then A is the cross section of the porous medium considered, and β is a coefficient of permeability.
Real processes are irreversible, and produce entropy. For a simple flow, the work loss to irreversibilities is
For an ideal gas flow, we have instead
Adiabatic Compressors, Turbines and Pumps
In a turbine, high pressure flow drives propeller blades that are attached to a rotating shaft. The flow does work on the blades, the rotating shaft delivers the work to the surroundings. As the flow does work, the pressure drops, that is turbines are driven by pressure differences. Compressors perform the opposite task: the shaft is driven, and the rotating blades pressurize the flow: compressors create a pressure difference and consume work.
The flow through most turbines (T ) and compressors (C), as sketched in Fig. 9.6, is so fast that there is no time to exchange heat with the surroundings, and thus they are often treated as being adiabatic. Although the flows are fast, the flow velocities are normally ignored, since the kinetic energy does not contribute significantly to work. With these simplifications (9.15, 9.16) reduce to
which hold for reversible and irreversible adiabatic turbines and compressors. In reversible adiabatic compressors and turbines the flow is isentropic (con-
tinuous lines 1-2s), while in irreversible adiabatic compressors and turbines the entropy must grow (dashed lines 1-2s), as illustrated in the figure.
Pumps serve to increase the pressure in liquids. Many liquids can be assumed to be incompressible in good approximation, so that v = const. The reversible pump work can then easily be computed from the flow work (9.24),